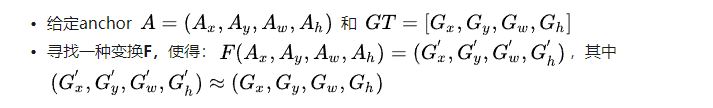本文主要是介绍计算机视觉算法整理(一):Faster RCNN,bounding box regression,IOU,GIOU,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
专门收录一下一些有趣的,计算机视觉中我想记录一下的算法,重点关注的是loss function,顺便说下相关算法。因为是收录,只为日后查看之需,有一些会借用一些资料,我会给出引用。
1、Faster RCNN
两阶段目标检测的代表作,可以说是开创了目标检测的一番局面。现在很多公司实际在商用的目标检测算法,依然很多是基于Faster RCNN的。虽然后来各种论文都号称吊打Faster RCNN,但是实际上往往是调参下的结果(有很多,但不是全部)。如果对Faster RCNN也进行细致调参,替换更好的预训练backbone,以及进行样本均衡、难负样本挖掘(hard negtive mining)、loss优化等技术,往往可以得到不错的结果。
经过R-CNN和Fast RCNN的积淀,Ross B. Girshick在2016年提出了新的Faster RCNN,在结构上,Faster RCNN已经将特征抽取(feature extraction),proposal提取,bounding box regression(rect refine),classification都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显[1]
。
总体结构

图1
Faster RCNN其实可以分为4个主要内容[1]:
- Conv layers。作为一种CNN网络目标检测方法,Faster RCNN首先使用一组基础的conv+relu+pooling层提取image的feature maps。该feature maps被共享用于后续RPN层和全连接层。
- Region Proposal Networks。RPN网络用于生成region proposals。该层通过softmax判断anchors属于positive或者negative,再利用bounding box regression修正anchors获得精确的proposals。
- Roi Pooling。该层收集输入的feature maps和proposals,综合这些信息后提取proposal feature maps,送入后续全连接层判定目标类别。
- Classification。利用proposal feature maps计算proposal的类别,同时再次bounding box regression获得检测框最终的精确位置。
对Faster RCNN的更详细的一个结构图如下:
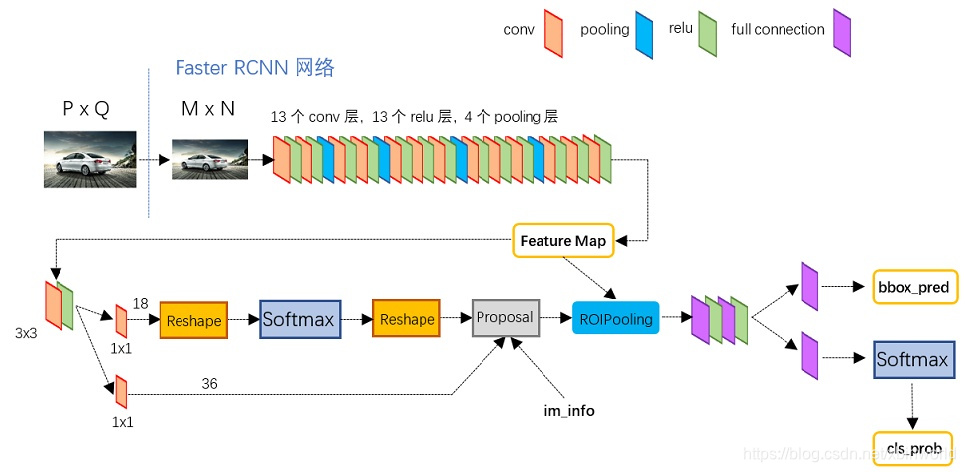 图2
图2
上图展示了python版本中的VGG16模型中的faster_rcnn_test.pt的网络结构,可以清晰的看到该网络对于一副任意大小PxQ的图像,首先缩放至固定大小MxN,然后将MxN图像送入网络;而Conv layers中包含了13个conv层+13个relu层+4个pooling层;RPN网络首先经过3x3卷积,再分别生成positive anchors和对应bounding box regression偏移量,然后计算出proposals;而Roi Pooling层则利用proposals从feature maps中提取proposal feature送入后续全连接和softmax网络作classification(即分类proposal到底是什么object)[1]。
说实话,Faster RCNN整个端到端流程非常复杂,并不是一下子发明的,首先其集成了大量以往CV领域的成熟技术,比如NMS去重框,以及继承了RCNN,Fast-RCNN发展过来的思路,还有提出Anchor技术,有点集大成的感觉。这些想要细看的同学推荐去看下原论文,以及帖子:Fast R-CNN文章详细解读,以及一文读懂Faster RCNN。记得我自己16年看的时候也是费了不少劲,这里先不赘述了。
bounding box regression
我要重点记录的是 bounding box regression,以及其loss。bounding box regression主要是用来修正anchors(基准框)获得精确的proposals(预测的物体框)。字面意思,regression就是说是要预测出bounding box的位置,所以后面肯定得跟一个回归loss,下面会说。注意的是,bounding box regression在图2的流程中实际上用了两次,一次在proposal框的地方,一次在后面bbox_pred的地方。可以看做第一次是粗调,后一次是细调。
下图所示绿色框为飞机的Ground Truth(GT),红色为提取的positive anchors,即便红色的框被分类器识别为飞机,但是由于红色的框定位不准,这张图相当于没有正确的检测出飞机。所以我们希望采用一种方法对红色的框进行微调,使得positive anchors和GT更加接近。w

图3
对于窗口一般使用四维向量[x,y,w,h]表示,分别表示窗口的中心点坐标和宽高。对于图 3,红色的框A代表原始的positive Anchors,绿色的框G代表目标的GT,我们的目标是寻找一种关系,使得输入原始的anchor A经过映射得到一个跟真实窗口G更接近的回归窗口G’,即:

图4
所以呢,dx(A),dy(A),dw(A),dh(A)这四个值就是要求的变换值,知道后就可以直接基于A框的原始位置得到G‘的位置。怎么得到这四个值呢?用regression!
形式如下[2]:

2、IOU,GIOU
IoU,又被称为Jaccard指数,是用于评估两个任意形状相似度的最常用指标,比如用于目标检测和图像分割中。对于如图1中的两个边界框A和B,我们计算出两者的交集I(红色部分),然后计算并集U,那么IoU就是两者的比值[3]:

图5
IoU编码的是两个边界框的形状性质,那么边界框的长,宽以及位置信息已经包含在内,所以说IoU是对物体尺度是不敏感的。而且IoU是一个归一化的指标,其值范围在[0,1]之间,当两个物体完全无交集时为0,而完全重叠时为1。所以IoU用于评价预测框和真实框的一致性是非常合适的。
而实际上主流的目标检测模型在训练时都是采用的回归损失,如L1和L2(Faster R-CNN采用smooth L1),我们来分析一下回归损失所面临的问题,边界框通常用左上和右下两个顶点来表示:(x1,y1,x2,y2)。下图给出了相同回归loss下边界框的差异性,其IoU值相差较大。

图6
其中绿色是真实框,而黑色是预测框,对于图6a,我们固定了两个框的左下顶点,同时固定了右上顶点的距离,此时预测框可以变化多测,但是L2损失是固定的。我们计算IoU值后发现也是变化非常大。同样的图6b可以看到L1损失存在类似的问题。这说明回归loss可能会陷入IoU指标的一个局部极值点。
(不过,也有一点牵强,比如上面写的Faster RCNN,并不是简单用顶点来回归的)
IoU loss已经被应用在图像分割中(与检测不太一样),IoU作为一种损失函数是可以进行BP的,因而可用于模型训练。但是IoU有一个致命的缺点,那就是当两个形状没有任何重叠时,IoU值为0,无法反映两个形状的具体偏差,而且梯度是0,无法对模型进行优化。图7可以展示这个问题,蓝色是真实框,图7a的黄色框和3的绿色框均与真实框没有交集,但是明显7b的预测更好,但是反映在IoU上均为0。

图7
由于IoU本身存在的问题,论文据此提出了一种新的指标:generalized IoU (GIoU),其计算公式如下:
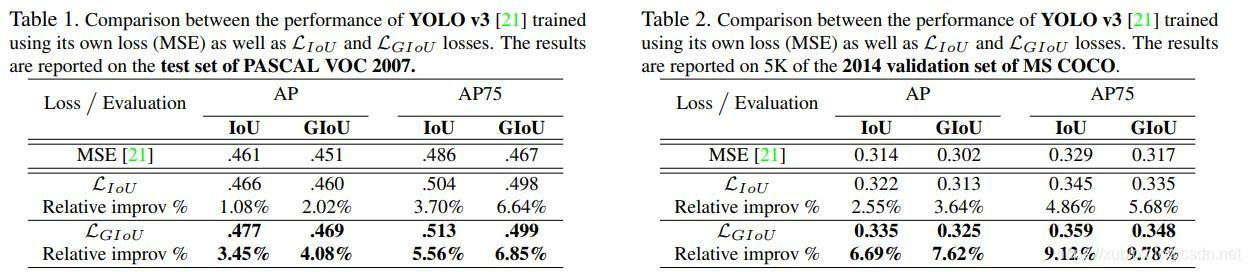
最重要的是GIoU会克服IoU的短板,当A和B完全不重合时,GIoU依然起作用。还是前面的例子如图8所示,可以看到图8a相比图b,C的大小较大,这样图8a的GIoU值是小于图b的,这说明GIoU对这种情况是可以处理的,虽然IoU值为0,但是当预测更好时,GIoU值是增加的。论文中以YOLOv3和Faster R-CNN进行实验,发现采用GIoU作为边界框loss,效果有提升。

图8
参考资料
[1] https://zhuanlan.zhihu.com/p/31426458
[2] https://blog.csdn.net/liuxiaoheng1992/article/details/81779474
[3] 另辟蹊径!斯坦福大学提出边界框回归任务新Loss:GIoU
[4] Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
[5] Generalized Intersection over Union(GIOU)论文核心思想解读笔记
[6] 白话mAP
这篇关于计算机视觉算法整理(一):Faster RCNN,bounding box regression,IOU,GIOU的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!