高斯金字塔 拉普拉斯金字塔_金字塔制造者

Recursion is beautiful, and when applied in combination it is truly a form of art. In this story, we are going to implement an interesting algorithm to create pyramids with recursion.

递归是美丽的，结合使用它确实是一种艺术形式。 在这个故事中，我们将实现一个有趣的算法来创建具有递归的金字塔。

Ancient civilizations around the world have built giant pyramids for worship and other holy purposes. The most famous, perhaps, are the pyramids built by the Egyptians. These huge structures are built with white, limestone surfaces so that they appear to be shining when seen from a distance. They are so magnificent, in fact, that many people today still believe that they were built by the aliens. So, today we are going to build them in code with recursion. It is very fitting.

世界各地的古代文明都建造了巨型金字塔，以供崇拜和其他神圣用途。 也许最著名的是埃及人建造的金字塔。 这些巨大的建筑物是用白色石灰石表面建造的，因此从远处看时它们看起来像是在发光。 实际上，它们是如此的宏伟，以至于当今许多人仍然相信它们是由外星人建造的。 因此，今天我们将使用递归代码构建它们。 非常合适。

问题： (Problem:)

Suppose I am given a base like this:

假设给我这样的基础：

[a, b, c ]

[a，b，c]

and that the following triangles are allowed:

并且允许以下三角形：

[aab, bdc, bad]

[AAB，BDC，坏]

what kind of pyramids can I create?

我可以创建哪种金字塔？

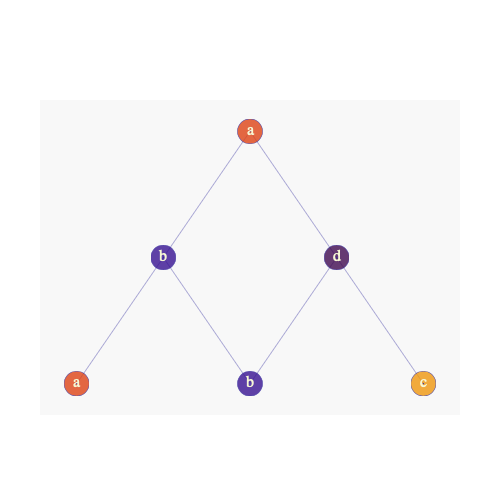
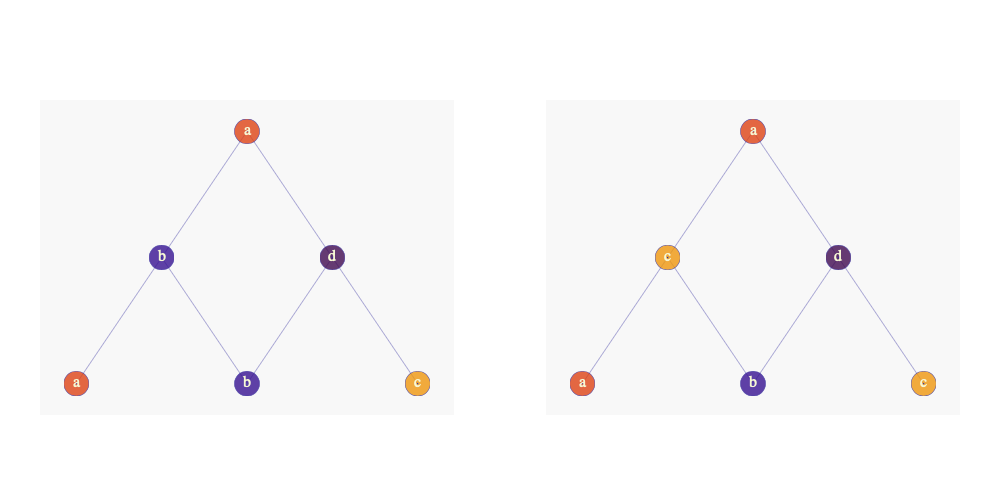
Shown above is a valid pyramid that can be built with the specifications given. The base is [a, b, c], and there are 3 triangles in this pyramid:

上面显示的是可以使用给定规格构建的有效金字塔。 底数为[a，b，c]，此金字塔中有3个三角形：

from bottom to top: [abb, bdc, bad]

从下到上：[abb，bdc，坏]

They are all in the allowed triangles.

它们都在允许的三角形中。

What if I add one more allowed triangle: acb?

如果我再添加一个允许的三角形：acb怎么办？

Well, if you did that you could get into this situation:

好吧，如果您这样做，可能会遇到这种情况：

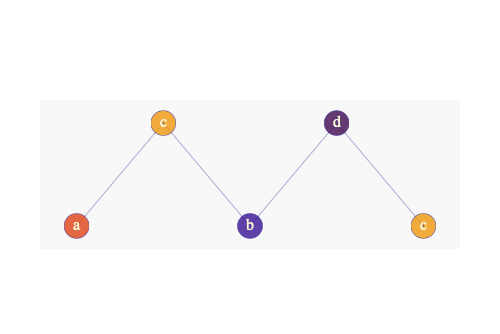
But there’s no way for you to complete the pyramid, because there is no allowed triangle that satisfies: c*d.

但是您无法完成金字塔，因为没有允许的三角形满足：c * d。

But if you add yet one more allowed triangle: cad

但是，如果再添​​加一个允许的三角形：cad

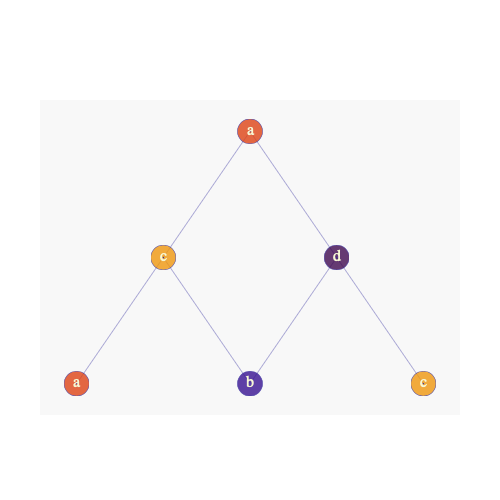
Then you can complete a new pyramid!

然后，您可以完成一个新的金字塔！

解决： (Solve:)

行制造商： (Row Maker:)

How do we go about creating all of the possible pyramids from a base, [a, b, c], and a set of allowed triangles, [abb, bdc, bad, acb, cad]?

我们如何从一个底数[a，b，c]和一组允许的三角形[abb，bdc，bad，acb，cad]创建所有可能的金字塔？

I think it’s clear that you’ll have to loop through each pair of base nodes, [ab, bc], and create the next rows of the pyramids (that would be [b, d] and [c, d]). So let’s do that.

我认为很明显，您必须遍历每对基本节点[ab，bc]，并创建金字塔的下一行(即[b，d]和[c，d])。 因此，让我们这样做。

Starting with ab, we check what are the allowed triangles with base ab. That would be: [abb, acb], at this point it’s clear that there are at least two possible combinations of next row, so how do you proceed to find all of them? Well, what we could do is recursively find the next row for the remaining base: [b, c], and then append the solutions to that to each of the possible first triangle. In this case the solutions to [b, c] is simple, there is only one: [bdc], so we append this solution to the two possible solutions to the first triangle ([abb, acb]), and contruct the two possible next row: ([b, d], [c, d])

从ab开始，我们检查以ab为基础的三角形是什么。 那应该是：[abb，acb]，这时很显然下一行至少有两种可能的组合，那么如何继续查找所有这些呢？ 好吧，我们可以做的是递归地找到剩余基数的下一行：[b，c]，然后将解决方案附加到每个可能的第一个三角形上。 在这种情况下，[b，c]的解很简单，只有一个：[bdc]，因此我们将此解附加到第一个三角形的两个可能解中([abb，acb])，并构造两个可能的解下一行：([b，d]，[c，d])

def row_maker(bottom, allows):

    if len(bottom) <= 1:
        return [bottom]

    def get_allowed(pair):

        allowed = []
        for allow in allows:
            if allow[0] == pair[0] and allow[-1] == pair[-1]:
                allowed.append(allow[1])

        return allowed

    allowed = get_allowed(bottom[:2])
    if len(bottom) == 2:
        return allowed

    substrings = row_maker(bottom[1:], allows)
    res = []
    for allow in allowed:
        for substring in substrings:
            res.append(allow + substring)

    return resbase = 'abc'
allows = ['abb', 'bdc', 'bad', 'acb', 'cad']

row_maker(base, allows)
# ['bd', 'cd']

Now that we have the next row maker function, we still need to construct the pyramid.

现在我们有了下一个行生成器功能，我们仍然需要构造金字塔。

金字塔制作器： (Pyramid Maker:)

In order to do that, again we start with the base [a, b, c], find the next rows: [b,d], [c, d], then for each of the next rows we again recursively find their respective next rows: [a], [a], and combine them into the final solutions:

为此，我们再次从基础[a，b，c]开始，找到下一行：[b，d]，[c，d]，然后对于接下来的每一行，我们再次递归地找到它们各自的接下来的行：[a]，[a]，并将它们合并为最终解决方案：

def pyramid_maker(bottom, allows):

    if len(bottom) <= 1:
        return [[bottom]]

    rows = row_maker(bottom, allows)

    res = []
    for row in rows:
        res = res + pyramid_maker(row, allows)

    res = [[bottom] + s for s in res]

    return resbase = 'abc'
allows = ['abb', 'bdc', 'bad', 'acb', 'cad']

res = pyramid_maker(base, allows)
# [['abc', 'bd', 'a'], ['abc', 'cd', 'a']]

Isn’t it wonderful?

这不是很好吗？

复杂： (Complexity:)

Before we go for dinner, what is the complexity of this algorithm?

在我们共进晚餐之前，该算法的复杂性是什么？

Let’s start with row_maker, in order to make the next row you are looping through every character of the current row, so that’s O(n) where n is the length of base.

让我们从row_maker开始，为了制作下一行，您正在遍历当前行的每个字符，因此为O(n)，其中n是基数的长度。

Moving onto the pyramid_maker. In it, you first call row_maker to get all of the possible rows, if allows is size m, the maximum number of possible rows returned are m^(n-1) and for each of those rows you call pyramid_maker again, until the returned rows are length 1. so the total number of operations are m^(n-1) * m^(n-2) * … * m¹ = m^(n(n-1)/2)

移动到pyramid_maker。 在其中，您首先调用row_maker以获取所有可能的行，如果允许的大小为m，则返回的最大可能行数为m ^(n-1)，对于这些行中的每一行，您再次调用pyramid_maker，直到返回行的长度为1。因此操作总数为m ^(n-1)* m ^(n-2)*…*m¹= m ^(n(n-1)/ 2)

The maximum complexity is actually:

实际上，最大复杂度是：

O(m^(n²))

O(m ^(n²))

That’s a pretty large number… but it’s really only for special cases where all the characters in the pyramid and allows are identical, so don’t worry too much about it!

这是一个相当大的数字……但实际上仅适用于特殊情况下，金字塔和允许的所有字符都相同，因此不必为此担心太多！

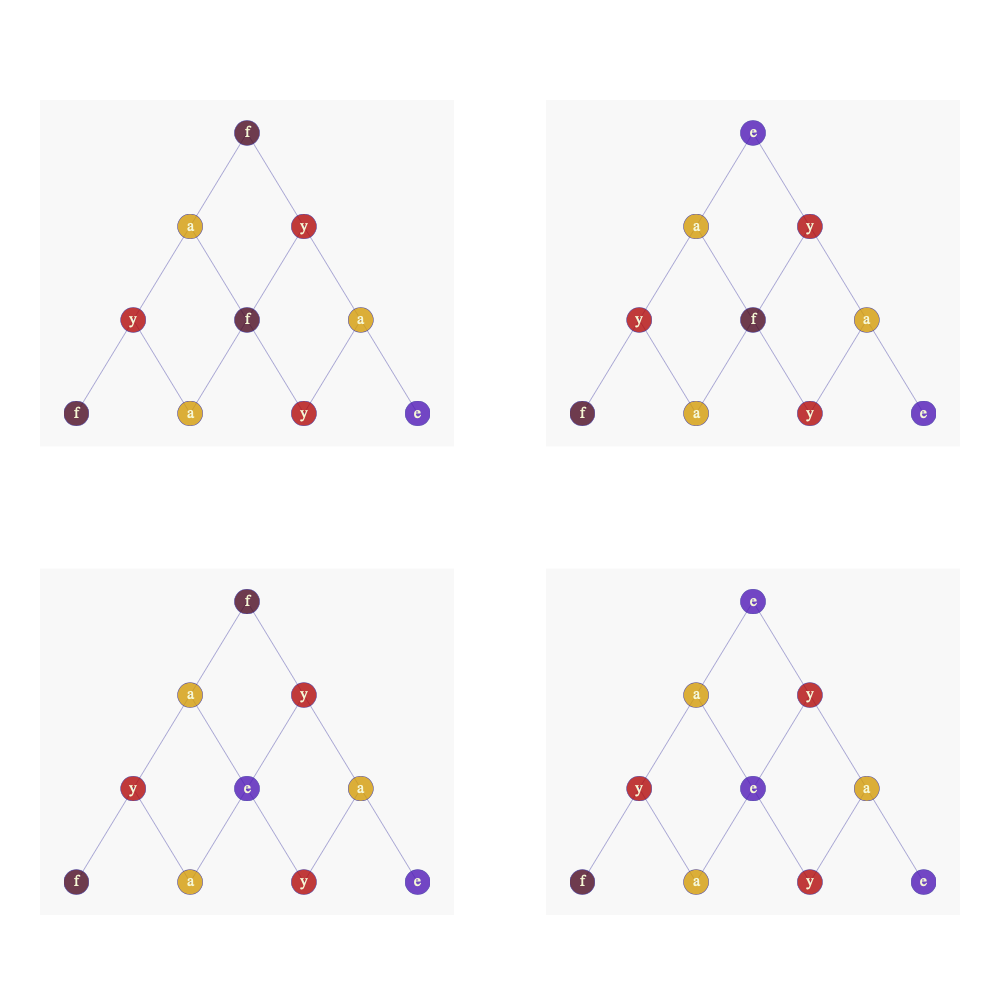
艺术时间！ (Art Time!)