入阵曲 洛谷p3941

题目描述

小 F 很喜欢数学，但是到了高中以后数学总是考不好。

有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的 时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以 解决的问题，被一个又一个算法轻松解决。

小 F 当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。

一年过去了，想想都还有点恍惚。

他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不 已。也许，这就是热血吧。

也就是在那个时候，小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的 第 $10^{100}$ 项，真是奇妙无比呢。

不过，小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小 问题。他写写画画，画出了一个 $n\times m$ 的矩阵，每个格子里都有一个不超过 $k$ 的正整数。

小 F 想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是 $k$ 的倍数？ 如果把一个子矩形用它的左上角和右下角描述为 $(x_1,y_1,x_2,y_2)$，其中$x_1\le x_2,y_1\le y_2$； 那么，我们认为两个子矩形是不同的，当且仅当他们以 $(x_1,y_1,x_2,y_2)$ 表示时不同；也就是 说，只要两个矩形以 $(x_1,y_1,x_2,y_2)$ 表示时相同，就认为这两个矩形是同一个矩形，你应该 在你的答案里只算一次。

输入输出格式

从标准输入中读入数据。

输入第一行，包含三个正整数 $n,m,k$。

输入接下来 $n$ 行，每行包含 $m$ 个正整数，第 $i$ 行第 $j$ 列表示矩阵中第 $i$ 行第 $j$ 列 中所填的正整数 $a_{i,j}$。

输出到标准输出中。

输入一行一个非负整数，表示你的答案。

输入输出样例

2 3 2 
1 2 1 
2 1 2

6 

说明

【样例 1 说明】

这些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表：

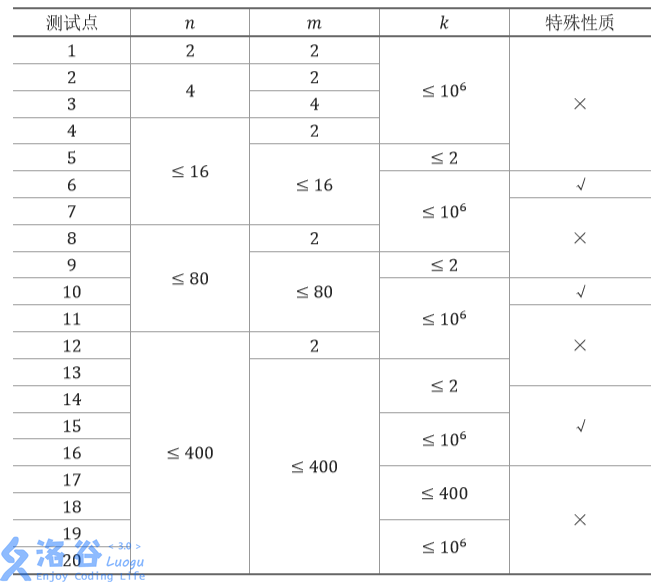
特殊性质：保证所有 a_{i,j}

${}_{i,j}$ 均相同。

[l])%k=0,那么sum[r]==sum[l] (mod p),所以只需统计前缀和中modk相同的数的对数，直接对每个余数统计个数就好了。

注意要考虑mod k=0的情况，解决方法是一开始另num【0】=1。

二维的情况也是一样，先枚举连续的列，然后压成一行就可以了。

#include<iostream>
#include<cstdio>
#include<cctype>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=405;
int a[MAXN][MAXN];
int n,m;
long long ans,vis[1000005],sum[MAXN][MAXN];
int read()
{long long x=0,ff=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')ff=-1;ch=getchar();}while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}return x;
}
int main()
{//ios::sync_with_stdio(false);int i,j,k,l,r;cin>>n>>m>>k;f(i,1,n){f(j,1,m){a[i][j]=read();sum[i][j]=(sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j])%k;}}vis[0]=1;f(l,1,n){f(r,l,n){f(i,1,m){ans+=vis[(sum[r][i]-sum[l-1][i]+(k<<1))%k]++;}f(i,1,m){vis[(sum[r][i]-sum[l-1][i]+(k<<1))%k]--;}}}cout<<ans<<endl;return 0;
}