本文主要是介绍斯坦福大学-自然语言处理入门 笔记 第十八课 排序检索介绍(ranked retrieval),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、介绍
- 之前我们的请求都是布尔类型。对于那些明确知道自己的需求并且了解集合体情况的用户而言,布尔类型的请求是很有效的。但是对于大部分的其他用户而言,布尔请求的问题是:大部分用户不熟悉布尔请求;布尔请求比较复杂;布尔请求的结果不是太多就是太少。排序检索应运而生。
- 排序检索返回的是排序好的文档结果,它可以很好地处理布尔请求以及自由文档请求(free text queries),即自然语言的请求。而我们也不需要担心太多的请求结果会导致我们用户体验不良,我们可以只给出前几名的检索结果。
- 排名的依据就是分数,设定一个0-1之间的数代表分数,分数度量的是文档和请求的契合程度。一个最简单的分数是:当我们请求是一个项的时候,直接把文档中项出现的次数作为分数的依据,次数越高分数越高。
- 下面会介绍一些算分的方法。
二、计算分数的方法
1、Jaccard 系数
- 一个比较常见的度量的两个集合的相似程度的方法是Jaccard 系数,系数范围是0-1,公式是jaccard(A,B) = |A ∩ B| / |A ∪ B|。
- jaccard(A,A) = 1
- jaccard(A,B) = 0 if A ∩ B = 0
- A和B不需要元素数量一致。
- 一个计算的例子:可以看到Jaccard 系数会比较偏向比较短的文档

- Jaccard系数的问题:
- 它没有考虑到项的频率(term frequency),也就是在文档中项出现的次数。因为在集合中比较稀有的项含有的信息量比常见的项更多,但是Jaccard系数没有考虑到这个问题。
- 我们需要更好的方法来对长度进行标准化,在后面的介绍中,我们会使用下面的公式来替代之前的公式。
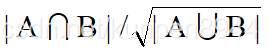
- 我们需要更好的方法来对长度进行标准化,在后面的介绍中,我们会使用下面的公式来替代之前的公式。
- 它没有考虑到项的频率(term frequency),也就是在文档中项出现的次数。因为在集合中比较稀有的项含有的信息量比常见的项更多,但是Jaccard系数没有考虑到这个问题。
2、项频率权重
- 项文档计数矩阵:每一列表示一个文档,每一行表示一个单词,每一格表示在这个文档中单词出现的次数。
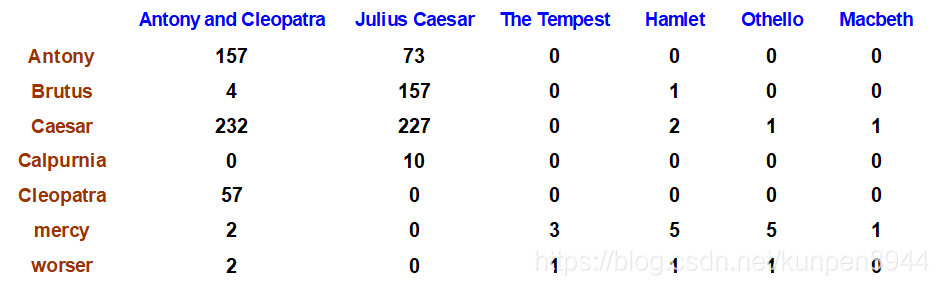
这种对文档的表现方法会存在一些问题,比如说John is quicker than Mary和Mary is quicker than John表达的意思不同,但是表现出来的矩阵是一样的。在后面的章节中我们会介绍用位置信息来修正这个问题。 - 但是需要关注的一个问题是,文档和请求的相关性与文档中请求项(term)的出现次数并不是线性相关的,而是一个比线性增长更慢的增长曲线。所以不能直接使用对计数信息,而是需要进行转化。计算方法如下:tf表示在文档d中出现t的次数,w表示修正后的结果。
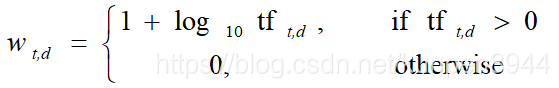 而文档的分数就是这些结果之和
而文档的分数就是这些结果之和
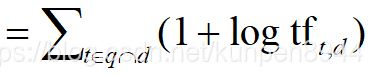
3、逆文档频率权重
- 因为在集合中比较稀有的项含有的信息量比常见的项更多。如果一个项在每个文档中都会出现的话,其实这个项就没有什么意义了。所以我们希望能有东西体现项的稀有性,于是出现了文档频率权重。
- 文档频率权重的计算公式如下:N表示中所有的文档数量,df表示文档中包含t的文档数量。对其取对数是希望降低df量级的影响。这个公式计算出来的指标,对越少见的项越高。
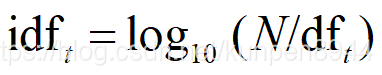 - 文档频率权重对一个项的请求是无效的,但是对两个及其以上的项的请求可以调整每个项得分的权重。比如对buy insurance,会加重对insurance的权重。
- 文档频率权重对一个项的请求是无效的,但是对两个及其以上的项的请求可以调整每个项得分的权重。比如对buy insurance,会加重对insurance的权重。 - 为什么使用文档频率而不是集合体频率?所谓的集合体频率指的是在集合中这个项总的出现的次数。这里存在的问题是有些单词可能在只在几个文档中出现,但是在这些文档中会反复出现;而有些单词会在每篇文档中出现,但是 文档只出现一次。这就和之前的那种单词性质不同,所以使用文档频率不合适。

4、tf-idf
- 将之前我们讨论的项频率权重(tf)和逆文档频率权重 (idf)相乘就可以得到tf-idf权重
- 这是信息检索领域最为著名的重要度度量,当某个token在单一文档中出现频率越高,就越重要;当某个token在集合体中出现的越少,那么就越重要。
- 对于一个文档对请求的评分就是这个文档关卡与请求词组的向量的加总。公式如下
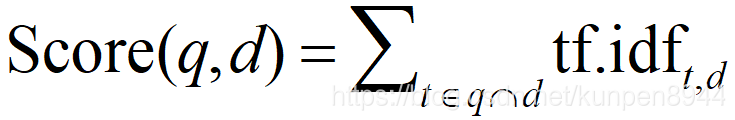
三、向量空间模型(VSM)
- 将文档和请求分别看成两个向量,计算两个向量的相似性
- 计算两个向量的相似性,欧氏距离不是一个好选择。因为当两个向量的长度不同时,它们的距离就会很大。比如下面的请求q是需按照同时含有GOSSIP和JEALOUS的文档,从图上来看d2是和他最相似的,但是欧氏距离上却是最远的。

- 但是当文档和请求相似的时候他们的夹角就会变小的。所以我们可以用文档向量和请求向量之间夹角的大小来给文档进行打分。当夹角为0的时候,相似度是最高的。
- 因为cosine是在[0,180]单调递减的(如下图),我们可以用cosine来表示相似度。
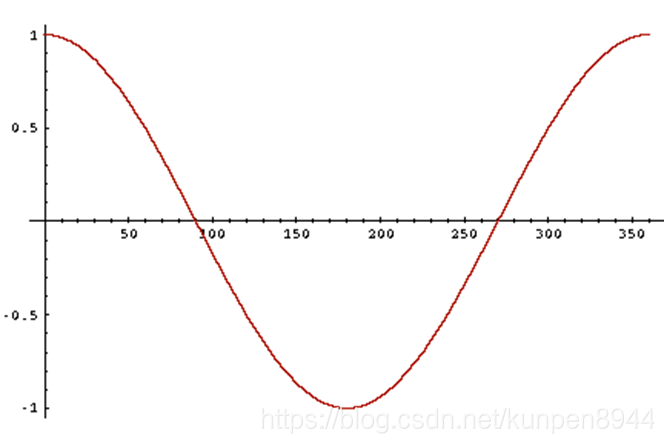 - 向量可以用它的长度进行标准化,从而转化成为一个单位向量(unit vector)。这样子的话就可以消除向量的长度带来的影响,长短向量之间就可比了。向量的长度计算就是它的L2范式。
- 向量可以用它的长度进行标准化,从而转化成为一个单位向量(unit vector)。这样子的话就可以消除向量的长度带来的影响,长短向量之间就可比了。向量的长度计算就是它的L2范式。 - 关于相似度的cos计算,公式如下:其中qi表示请求中项i的tf-idf重要性,di表示文档中项i的tf-idf重要性。cosine就是q和d的相似度,也就是q和d的夹角的cosine值。
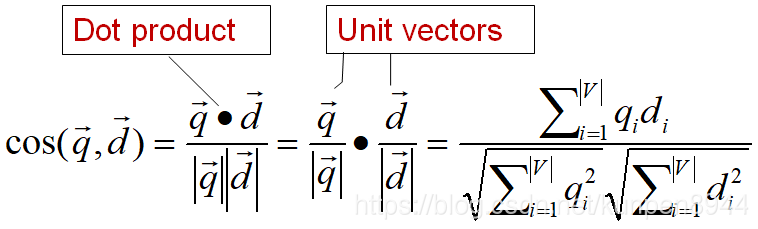 如果向量本身是长度标准化的话,cosine相似度就直接是点积,公式见下,其中q和d都是长度标准化的。
如果向量本身是长度标准化的话,cosine相似度就直接是点积,公式见下,其中q和d都是长度标准化的。
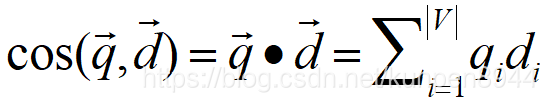 - 一个计算的例子:比较简奥斯丁的三部作品(情感与理智,傲慢与偏见和呼啸山庄)的相似度。第一步是计算对应的tf。
- 一个计算的例子:比较简奥斯丁的三部作品(情感与理智,傲慢与偏见和呼啸山庄)的相似度。第一步是计算对应的tf。
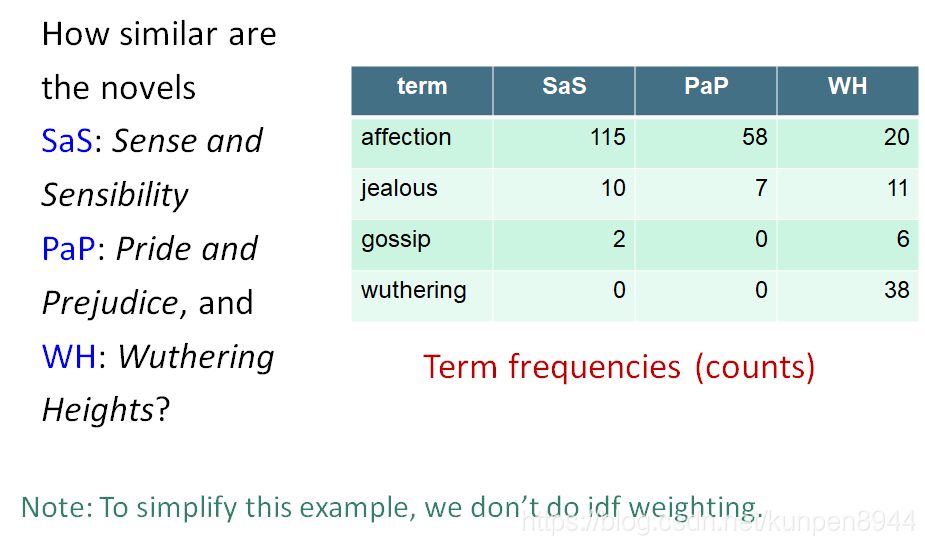
接下来,对tf取对数;然后,进行长度标准化;接下来计算cosine。
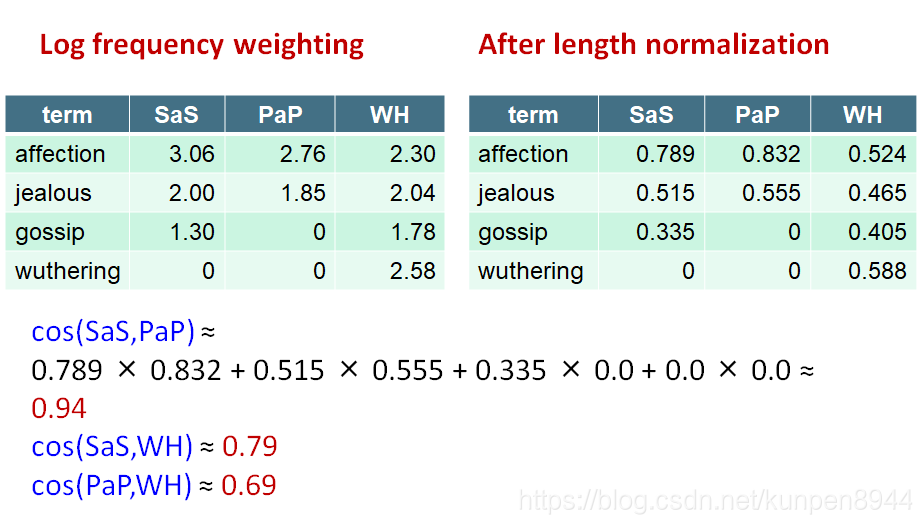
四、一个计算tf-idf的cosine的例子
- tf-idf重要性有很多的变种。

- 很多的搜索引擎允许对请求和文档采取不同的重要性计算方法。这些计算方法可以用上表中的首字母缩写表示,形如ddd.qqq前三个字母表示对文档的三个处理方法,后三个表示对请求的三个处理方法。
- 一个比较标准的重要性计算框架是Inc.ltc。对文档的处理是对数tf,不进行idf,进行cosine标准化。对请求的处理是对数tf,idf,然后进行cosine标准化。
- 一个具体的Inc.ltc的例子
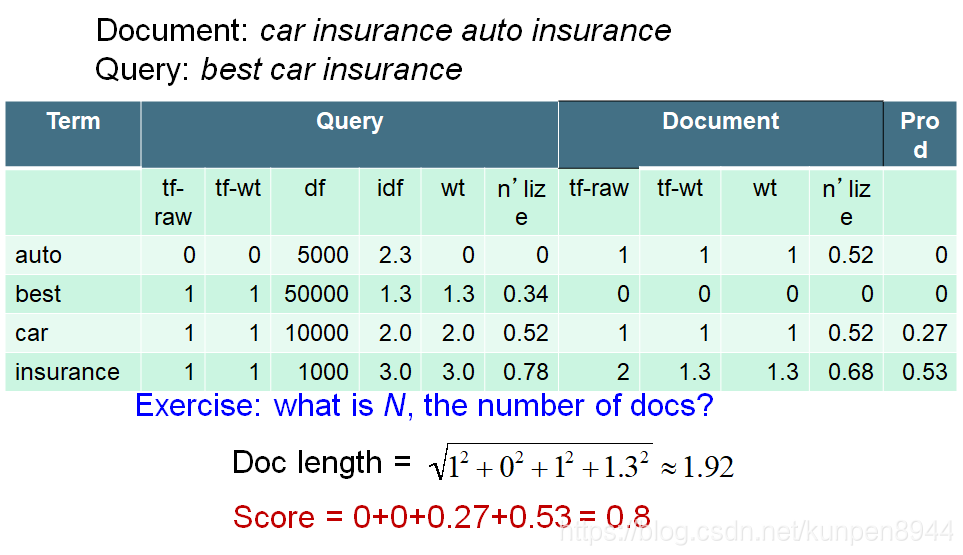
- 计算cosine得分的代码:这是一个基本的算法,在实际的应用中会有更高效的算法

五、搜索引擎评价
- 搜索引擎是有很多方面的,比如索引多快,搜索多快,对请求的包容度,UI,是否免费等等
- 但是其中最重要的是用户的幸福程度(happiness),搜索速度和包容广度是一些因素,但是更重要的是度量结果和用户信息需求的相关性
- 信息需求是被翻译成了请求,但是信息需求不等于请求,比如我们想知道相比于白酒红酒是否可以帮助我们更有效地低于心脏病风险,那么我们的请求可能是:红酒心脏病有效,而不是前面的那句话。所以我们评估的是文档是否针对的是那些信息需求,而不是是否含有请求的项。
- 评估排序结果
- 评估需要的材料如下,随后像之前一样计算precision/recall/f值
- 基准文档集合
- 一系列基准请求
- 文档与请求是否相关的判断
- 如何评估排序结果
- 系统可能会返回任何数目
- 通过改变我们取的返回结果的个数(recall的水平),我们可以得到一个precision-recall 曲线。
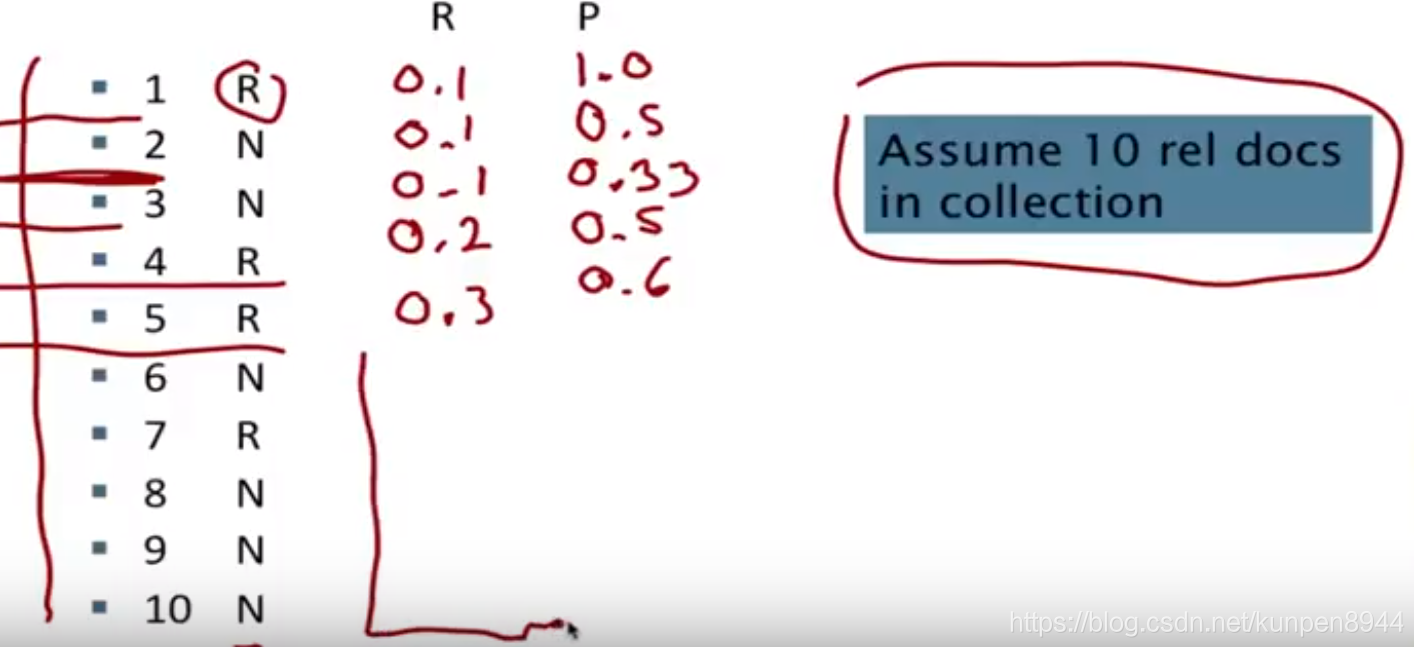
- 另一种评估方法:Mean average precision(MAP)
- AP:每检索到一个相关的文档,就对之前所有的文档计算一次precision,然后算所有precision的平均值
- 一般会使用固定的recall水平,也就是计算前K个检索结果的AP
- 对一系列请求的MAP就是对每个请求的AP计算算术平均
- 一个计算AP的例子

- 评估需要的材料如下,随后像之前一样计算precision/recall/f值
这篇关于斯坦福大学-自然语言处理入门 笔记 第十八课 排序检索介绍(ranked retrieval)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





