本文主要是介绍Breadth-First Search ------ 广度优先搜索算法(BFS),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Breadth-First Search ------ 广度优先搜索算法
所谓广度优先遍历,类似树的按层次遍历,就是一层一层的,向下遍历,层层堵截。
1.广度优先搜索的思想:
① 访问顶点vi ;
② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的
点的邻接点都被访问;
2.例子
广度优先遍历的结果是V1-- V2 -- V3 -- V4 -- V5-- V6 -- V7 -- V8。
说明:
为实现③,需要保存在步骤②中访问的顶点,而且访问这些顶点的邻接点的顺序为:先保存的顶点,其邻接点先被访问。 这里我们使用queue队列实现这种先进现出的服务。
过程:
1)将 V1 加入队列,取出 V1,并标记为 true (即已经访问),将其邻接点加进入队列,则队内顶点依次为[ V2 V3 ],访问的节点依次为:V1
2)取出 V2,并标记为 true (即已经访问),将其未访问过的邻接点 [ V4 V5 ] 加进入队列,则队内顶点依次为[ V3 V4 V5 ];访问的节点依次为:V1-- V2
3)取出 V3,并标记为 true (即已经访问),将其未访问过的邻接点 [ V6 V7 ] 加进入队列,则队内顶点依次为[ V4 V5 V6 V7 ] ;访问的节点依次为:V1-- V2 -- V3
4)取出 V4,并标记为 true (即已经访问),将其未访问过的邻接点 [ V8 ] 加进入队列,则队内顶点依次为[ V5 V6 V7 V8 ] ;访问的节点依次为:V1-- V2 -- V3 -- V4
5)取出V5,并标记为 true (即已经访问),因为其邻接点已经加入队列,则无节点入队,队内顶点依次为[V6 V7 V8] ;访问的节点依次为:V1-- V2 -- V3 -- V4 -- V5
6)取出V6,并标记为 true (即已经访问),因为其邻接点已经加入队列,则无节点入队,队内顶点依次为[V7 V8] ;访问的节点依次为:V1-- V2 -- V3 -- V4 -- V5 -- V6
7)取出V7,并标记为true(即已经访问),因为其邻接点已经加入队列,则无节点入队,队内顶点依次为[V8] ;访问的节点依次为:V1-- V2 -- V3 -- V4 -- V5 -- V6 -- V7
8)取出V8,并标记为true(即已经访问),因为其邻接点已经加入队列,则无节点入队,队内顶点依次为[] ;访问的节点依次为:V1-- V2 -- V3 -- V4 -- V5 -- V6 -- V7 -- V8
所以最终结果为:V1-- V2 -- V3 -- V4 -- V5 -- V6 -- V7 -- V8。
3.代码
为什么有第九行的 for 循环,是因为,防止已经第一次选取的u节点的全部相关节点遍历完后,仍然存在一些节点未曾访问到;
如果把第九行的 for 循环和第11行的 if 全部删除,把第一次进队的 v 直接初始化成 V1,也是错误的,原因就是上面那句话
#include <queue>
using namespace std;
....
void BFSTraverse(Graph G)
{//先将其所有顶点都设为未访问状态for (int v=0;v<G.vexnum;v++) visited[v]=false;queue<int> Q;for(int v=0;v<G.vexnum;v++) {if(visited[v]==false) //若该点没有访问{Q.push(v); //将其加入到队列中visited[v]=true;while (!Q.empty()) //只要队列不空,遍历就没有结束{int t =Q.front(); //取出对头元素Q.pop(); //弹出栈顶的元素printf(" %d ",t+1); //依次输出栈顶的元素就是依次遍历的顺序for(int j=0;j<G.vexnum;j++) //将其未访问过的邻接点加进入队列if(G.arcs[t][j]==1&&visited[j]== false){Q.push(j);visited[j]=true; //在这里要设置true,因为这里该顶点我们已经加入到了队列,为了防止重复加入!}}}}
}4.时间复杂度
数组表示:查找每个顶点的邻接点所需时间为O(n^2),n为顶点数,算法的时间复杂度为O(n^2)
5)应用
用于寻找两个顶点直接最短的距离 ,DFS算法不可
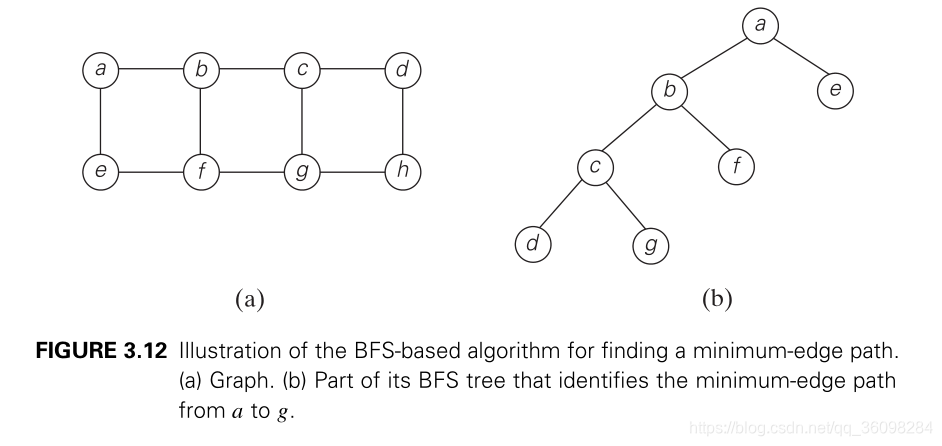
例如,bfs可用于查找两个给定顶点之间边数最少的路径。为此,我们在两个顶点之一处开始BFS遍历,并在到达另一个顶点时立即停止。
例如,图3.12中图表中的路径a−b−c−g在顶点a和g之间的所有路径中的边数最少。
参考:https://blog.csdn.net/wang725/article/details/82120428
这篇关于Breadth-First Search ------ 广度优先搜索算法(BFS)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





