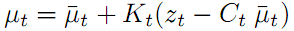本文主要是介绍卡尔曼滤波算法实例剖析--机器人足球赛场中的定位算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
卡尔曼滤波(Kalman filtering)最早在 阿波罗飞船 的导航电脑中使用,它对 阿波罗计划 的轨道预测很有用。 卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。是目前应用最为广泛的滤波方法, 在通信, 导航, 制导与控制等多领域得到了较好的应用。
卡尔曼滤波本身是贝叶斯滤波体系的,建立在马尔科夫概率模型基础上。大多数关于卡尔曼滤波的文章都是大量的数学概率公式,看的晕头转向。本文通过机器人足球场上的定位来通俗易懂的讲述该滤波算法原理。
1. 机器人足球场景介绍
如图1所示,踢球的机器人为差分轮式机器人,它可以直线或者弧线行走,也就是可以同时以线速度v和角速度ω行动。v和ω都是从传感器测量得到的,这里认为是已知的。
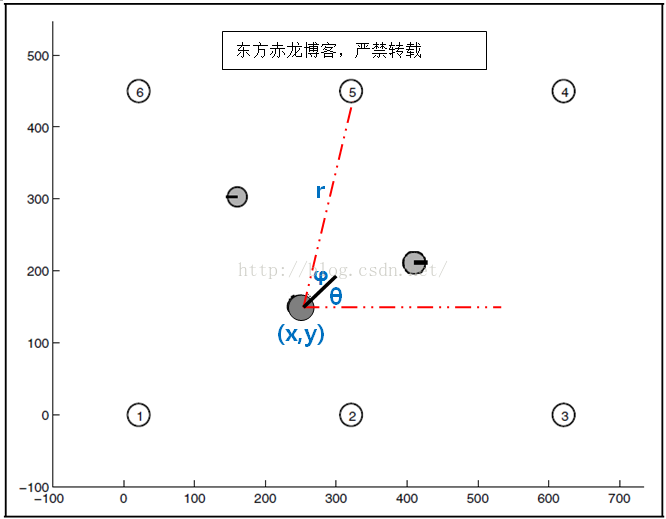
如图2,足球场为矩形,内部填充灰色的黑色圆圈代表机器人,它在场内的位置可以表示为(x,y),左下角为原点; 圆圈的黑色直线代表机器人的角度为 θ,以X轴正向为0度,逆时针旋转。
为了便于定位,四个角落和中间两边分别放置一个ROS的AR标签,这些标签完全不同,编号为 1-6, 位置在系统内已知固定。无论在场内任何地方,机器人使用Kinnect或XTionPRO 均可以探测到至少一个AR标签,ROS可以检测到距离AR标签的距离 r 和角度 φ. 它们也是实时获取的已知量。
很明显,角度θ+φ 是可以从机器人位置(x,y)和AR标签位置(mx,my)同反正切 atan2(mx - x ,my - y) 轻松计算出来。
图1 机器人足球场地实景图
图2 机器人足球场逻辑图
2. 卡尔曼滤波模型
在任何一个时间点t-1, 机器人的位置为(x, y,θ) , 它以线速度和角速度(vt,ωt)以弧线轨迹移动到下一个时间点t时,新的位置(x', y', θ')通过简单的三角函数数学公式是可以算出来的:
公式1 坐标转移矩阵
这个过程叫做状态转移,状态x=(x,y) 代表机器人的坐标(状态x 和坐标里面的x只是巧合同一个字母,因为卡尔曼滤波里面的状态就是用x表示的,不要混淆)。
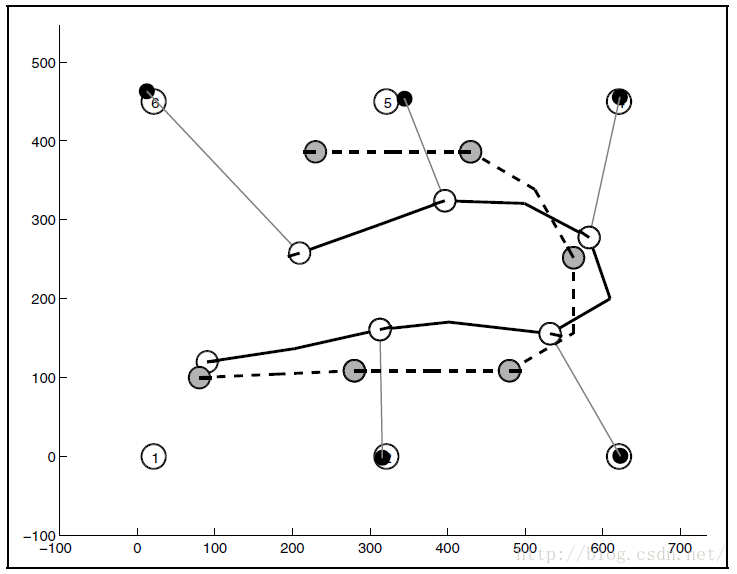
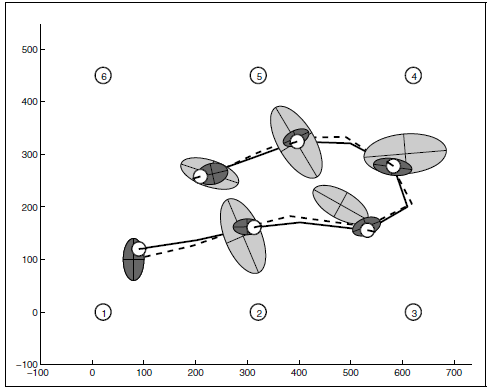
按照公式1不停地累计计算从t 到 t-1,再到t+2,......,t+n,貌似可以得到机器人的实际位置。但是实际效果是什么样子呢?来看一下图3,机器人从左下角开始移动6个时间点,依次经过AR标签2-6, 它的轨迹为实线,白色圆圈代表每个时间点的位置。 而根据公式1的方法计算得到的轨迹为虚线所示,灰色圆圈代表计算机算出的位置。可以清楚的看到,计算误差很大,从一开始的位置计算就有有误差,这种误差不断积累,最终‘失之毫厘,谬以千里’。
图3 移动机器人的计算轨迹(虚线)和实际轨迹(实线)有很大误差
这是为毛呢?原因就是目前所有人类制造的各种仪器都是有误差的。就像GPS定位一样,它也不是能够精确的给出一个坐标,它有个5米到10米的误差。同样机器人传感器得到的线速度v和角速度ω都是不准确的,有噪音。如图4所示,灰色圆圈为公式1计算出来的坐标,但是噪音范围为椭圆形所示,真实位置在里面的任何一点都是有可能的,只是每个点的概率不一样,中间的概率是最高的。
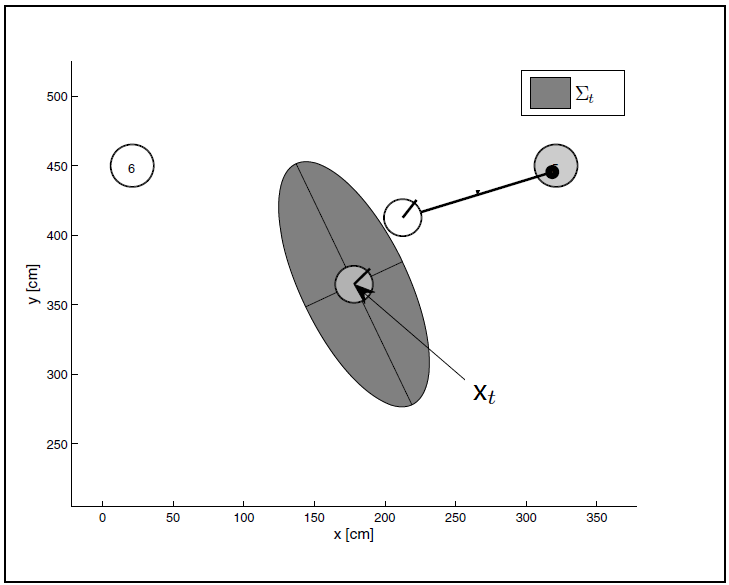
图4 测量误差--椭圆区域
2.1 卡尔曼滤波能做什么
看到这里会问了,不是还有AR标签帮助测量定位吗?根据标签位置,距离和角度也可以算出坐标啊! 没错,但是还是那个老问题,这个测量结果也是有误差的,误差大小完全取决于传感器。
我们总结一下,现在有两个已知量:
- 移动的速度和起点坐标 根据公式1算出来的坐标 x = (x,y) 有很大误差噪音
- AR标签测量的值 z=(r, φ) 有很大误差噪音
卡尔曼滤波能做什么?它可以根据上面的两个有噪音的测量值融合到一起获得最优的坐标,也就是最优状态。这就是一个降噪的过程,滤波出来的坐标也是有噪音的,但是很小。如图5所示,滤波后的轨迹和真实轨迹非常接近了。灰色椭圆是测量位置的噪音范围,黑色椭圆是卡尔曼滤波后的噪音范围,确实降噪了不少。
这个最优的坐标和噪音到了下一个时刻t+1,就作为滤波的输入结合t+1的AR标签观测量和噪音再次推导一遍。机器人不断行走,该算法不断的循环执行就推导出了最优的移动轨迹。每次间隔Δt越小,滤波的精度就越高。所以计算机性能越好,就可以越精确的估计移动轨迹。
图5 卡尔曼滤波效果图 移动机器人的计算轨迹(虚线)和实际轨迹(实线)非常接近
********接下来开始讲概率矩阵数学了,东方赤龙提醒您:不想看可以不看了*******
2.2 卡尔曼滤波模型参数定义
卡尔曼滤波是为了获取每个时刻t最优的状态,它有许多物理意义的参数:
- 状态 x = 坐标 (x,y,θ)
- 状态噪音Σ = 状态 x 的精确度
- 最优状态 μ 每个时刻卡尔曼滤波估算的最优坐标
- 状态转移控制量 u = 线速度和角速度(v, ω)
- 状态转移噪音 R 因为移动所增加的噪音
- 观测量 z = AR标签测量值 (r, φ)
- 观测量噪音 Q = AR标签传感器的噪音
还有几个状态转移方程:
- xt =At xt-1 +Bt ut 根据t-1的坐标和移动速度估计出在t时刻的坐标,也就是上面的公式一。这里At =1,Bt 就是时间间隔 Δt
- z =C x 状态量x 到观测量z 的映射关系。这里就是根据下面的三角函数计算出来的, C代表了状态映射矩阵。
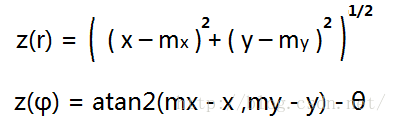
2.3 卡尔曼滤波过程
有了数据,接下来就是具体操作了。科尔曼滤波或者贝叶斯滤波体系的过程都包含两个步骤:
- t-1 到 t时刻的状态预测,得到前验概率
- 根据观察量对预测状态进行修正,得到后验概率,也就是最优值
在卡尔曼滤波里面,每个状态都是一个正态分布概率,也就是高斯分布概率:
p(x) = N( μ, σ )
这里,μ 就是高斯分布的均值,也就是概率最高的值,称为最优值。σ 就是高斯分布的方差,也就是噪音。所以卡尔曼滤波最终算出来的不是一个精确的状态值,而是一个概率最高的最优状态值。这个状态值在我们的例子里面就是坐标。
2.3.1 状态预测
根据t-1时刻的最优状态值 xt-1 ,带入文章开头的状态转移方程公式1,根据控制量u得到t时刻的新状态μ。就是根据机械运动的线速度和角速度推算出新的坐标 。为了便于记忆,我们一般化它为公式一:
。为了便于记忆,我们一般化它为公式一:
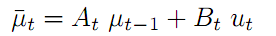
公式一 状态转移变换方程
上面已经说了,这个预测是有误差噪音的,在t-1时刻的噪音 Σt-1 经过状态转移后被扩大了,也就是说经过移动后,坐标的不确定性增大了。新的噪音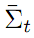 。为了便于记忆,我们一般化它为公式二:
。为了便于记忆,我们一般化它为公式二: 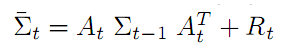
公式二 状态噪音转移变换方程
2.3.2 卡尔曼增益 K
公式三 卡尔曼增益K
卡尔曼增益 K 相当于一个系数变换矩阵,它包含了两个信息:
- 观测量 z 到状态量 x 的的变换矩阵,就是说 x = K z . 相当于2.1节提到的状态转移方程 z = C x 中 C 的逆矩阵。本文例子就相当于从地标AR标签的距离和角度反推出机器人的位置。
- 对观测量的可信度百分比。观测量可信度越高,也就是测量噪音Q相对于与状态预测噪音
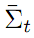 越小,该百分比就越高。反之则越低。
越小,该百分比就越高。反之则越低。
2.3.3 后验值修正
既然预测不准确,那就用测量后验值去修正它。先修正状态值x,就是公式四:
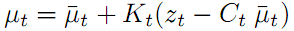
公式四 状态修正方程
公式五 状态误差噪音修正方程
修正后的噪音Σt 其值要比预测噪音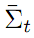 和感测噪音Q都要小。这样直观上也容易理解,滤波后的状态噪音最小,所以最优。
和感测噪音Q都要小。这样直观上也容易理解,滤波后的状态噪音最小,所以最优。
2.4 卡尔曼滤波总结
以上公式一二三四五,就是卡尔曼滤波的五项公式。前面说过,在卡尔曼滤波里面,每个状态都是一个正态分布概率,也就是高斯分布概率:
p(x) = N( μ, σ )
整个滤波过程从高斯曲线上看就如下图6所示:
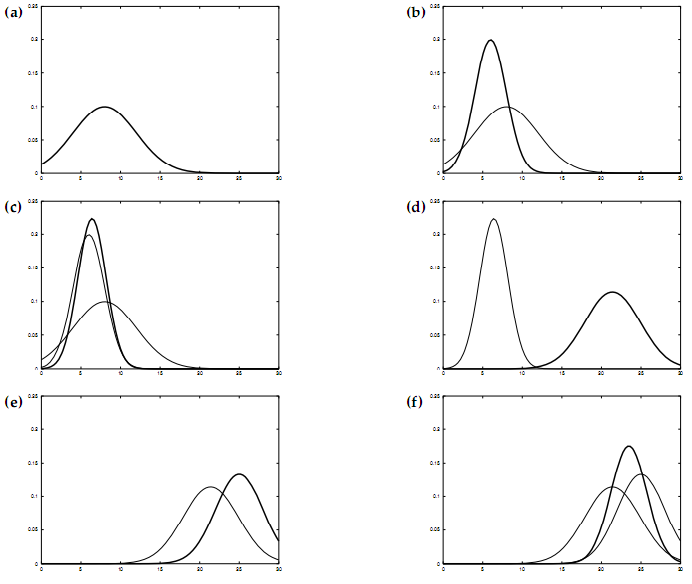
a) 初始时刻t-1的状态概率高斯分布,分布图的宽度越宽,误差越大,最优均值概率就越低。
b) t时刻观测到观测量概率高斯分布图,明显观测量噪音低,可信度高。但是两个高斯的均值不一致,就是说观测和预估不一致
c) 卡尔曼滤波后的高斯分布图,该高斯图的噪音比其它两个都小,最优均值概率高于其它两个高斯图,而均值恰好在其它两个高斯均值之间
d) t+1时刻发生的状态转移,状态向右移动,这个过程增加了新的噪音,所以新的状态高斯图噪音增大,最优均值概率下降
e) t+1时刻的观测量高斯分布图
f) t+1时刻应用卡尔曼滤波融合出来噪音低的最优状态高斯图
3 科尔曼滤波的条件和扩展卡尔曼滤波
本文的例子其实是个扩展卡尔曼滤波。标准的卡尔曼滤波要求2.2小节中的两个状态转移方程为线性方程,也就是要求A、B和C矩阵都为线性矩阵。 - xt = At xt-1 + Bt ut 根据t-1的坐标和移动速度估计出在t时刻的坐标,也就是上面的公式一。这里At =1,Bt 就是时间间隔 Δt
- z = C x 状态量x 到观测量z 的映射关系。这里就是根据下面的三角函数计算出来的, C代表了状态映射矩阵。
本文的例子明显不符合这个要求,因为涉及到了三角函数等计算。标准卡尔曼滤波在现实环境中是很难找到的,大部分情况下都是非线性状态转移。而扩展卡尔曼滤波就是应用在非线性状态转移的环境中的。它的算法和标准算法一样,只是把上面的A、B和C矩阵线性化,也就是用一个线性方程最大程度的逼近非线性方程。常用的方法有UT变换( Unscented Transformation) 和UKF变换。
ROS学习 ——使用rosinstall下载源文件
ROS的stack库分作两部分,一部分为核心部分,即main部分,简而言之就是使用下面命令,安装ROS系统时就已经安装到我们用户电脑上的那部分。 $ sudo apt-get install ros-diamondback-desktop-full
另一部分为选用部分,即universe部分,它不仅包括一些开源库的支持,如opencv,pcl,openni_kinect等,还有更上面以机器人功能模块命令的一些stack,例如pr2_doors,find_object,face recognition,grasp等等,真是一个丰富的宝藏,更详细的stack包可以在官网的StackList页面查询。(http://www.ros.org/wiki/StackList)
当然,除了随系统自动安装到我们客户端的那部分stack之外,当我们需要某特定功能的模块(如pr2_doors)时,此时,rosinstall就派上用场了,下面就简单以pr2_doors为例.
$ cp /opt/ros/diamondback/.rosinstall ~/stacks/pr2_doors.rosinstall //在stacks文件夹里面创建新的rosinstall文件
$ roslocate info pr2_doors >> ~/stacks/pr2_doors.rosinstall //此句是自动寻找pr2_doors信息
命令执行到这儿,打开pr2_doors.rosinstall,可以看到:

$ rosinstall ~/stacks ~/stacks/pr2_doors.rosinstall
$ source ~/stacks/setup.bash //为防止每次使用启动后都要重新编译,可将相应地址添到~/.bashrc中
$ rosmake .......(pr2_doors里面所需的package文件)
进一步的可以将下载后的stack目录(如 ~/stacks)添加到ROS_PACKAGE_PATH目录中,以后就能正常在原来的ROS系统下使用下载后的package了.在这里,感谢ROS论坛中提问和解惑的人们.
(本文方法参考以下网址:http://answers.ros.org/question/9197/for-new-package-downloading)
ROS 学习系列 -- 使用Rviz观察智能车的运动轨迹 无陀螺仪计算角度转动
视频录像
根据两边轮子转动的速率不同,推算出转动的角度。包括原地旋转。
计算的原理和代码可以查看文章 ROS 教程之 navigation : 用 move_base 控制自己的机器人(2)
这篇关于卡尔曼滤波算法实例剖析--机器人足球赛场中的定位算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



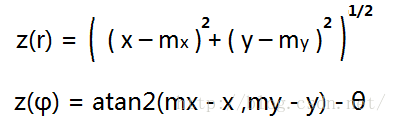
 。为了便于记忆,我们一般化它为公式一:
。为了便于记忆,我们一般化它为公式一:
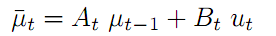
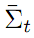 。为了便于记忆,我们一般化它为公式二:
。为了便于记忆,我们一般化它为公式二: 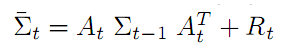
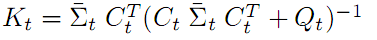
越小,该百分比就越高。反之则越低。
 正确,那它观测到AR标签时的距离和角度对应的值就是
正确,那它观测到AR标签时的距离和角度对应的值就是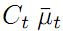 ,可视为预测观测值。而
,可视为预测观测值。而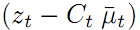 则代表预测观测值与实际观测值的差距。乘上卡尔曼增益K,就得到了修正量。修正量加上预测值就是修正值或最优值。假设
则代表预测观测值与实际观测值的差距。乘上卡尔曼增益K,就得到了修正量。修正量加上预测值就是修正值或最优值。假设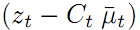 为0,就是说预测AR标签位置和观测到的AR标签位置完全一样,那公式四返回就是预测状态坐标值,和直观常识吻合的非常完美。假设
为0,就是说预测AR标签位置和观测到的AR标签位置完全一样,那公式四返回就是预测状态坐标值,和直观常识吻合的非常完美。假设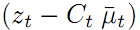 的值比较大,就是说预测AR标签位置和观测到的AR标签位置差别很大,那根据卡尔曼增益K中的百分比信息的小或大,公式四就返回值靠近预测值或靠近测量值多一些,和实际物理意义吻合的还是非常完美。
的值比较大,就是说预测AR标签位置和观测到的AR标签位置差别很大,那根据卡尔曼增益K中的百分比信息的小或大,公式四就返回值靠近预测值或靠近测量值多一些,和实际物理意义吻合的还是非常完美。 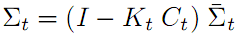
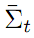 和感测噪音Q都要小。这样直观上也容易理解,滤波后的状态噪音最小,所以最优。
和感测噪音Q都要小。这样直观上也容易理解,滤波后的状态噪音最小,所以最优。