算法基础7 —— 二分算法 (二分模板 + 洛谷-A-B数对 + 蓝桥杯-分巧克力) + 浮点二分(求一个数的三次方根 + 剪绳子)

闲聊

在经典的软件开发过程中，编写程序所需要的工作量只占软件开发全部工作量的10%～20%。 《软件工程导论》—— 张海藩

总结

二分查找

问题引入：在如下数组中，查找数字4的下标 —— 3。为了方便起见，数组0元素的位置不存储数据。

考虑两种查找方法：

• 线性查找：从前往后遍历数组，找到第一个元素为4的位置，记录并输出即可(假设数组中的所有元素并不相同)。时间复杂度为O(n)
• 二分查找：时间复杂度为O(logn)
  ①初始时，设置两个指针L，R。L = 1，R = 8，Mid = (L + R) / 2 = (1 + 8) / 2 = 4(向下取整)
  
  ②比较此时Mid指针指向位置的元素与4的大小关系。arr[Mid] = arr[4] = 6 > 4，说明目标元素4的位置要在L -> Mid-1中找。此时令R = Mid - 1，即令R = 3(右指针左移)，更新Mid = (L + R) / 2 = (1 + 3) / 2 = 2
  
  ③再比较此时Mid指针指向位置的元素与4的大小关系。arr[Mid] = arr[2] = 3 < 4，说明目标元素4的位置要在Mid + 1 -> R中找。此时令L= Mid + 1，即令L = 3(左指针右移)，更新Mid = (L + R) / 2 = (3 + 3) / 2 = 3
  
  ④继续比较此时Mid指针指向位置的元素与4的大小关系。arr[Mid] = arr[3] = 4 = 目标元素4，查找结束。返回下标3

指针移动

二分查找的适用范围：单调不下降或单调不上升的数组a[1…n]或函数

如果x == a[mid] 则x在其中；

如果x < a[mid] 则x在[l，mid - 1]；

如果x > a[mid] 则x在[mid + 1,r];

• 当a[Mid] < 目标元素x时
  

• 当a[Mid] > 目标元素x时
  

二分模板

注：在使用二分模板时，需要保证关键字按大小有序排列(在上例中，元素按照递增顺序排列)

#include <iostream>using namespace std;const int N = 110;
int a[N];int binarySearch(int a[],int n,int x)//其中n表示数组的长度,x表示要查找的目标元素
{int L = 1,R = n;int ans = -1;//ans用来记录查找要查找元素的下标(一般设置为负数)while (L <= R)//二分查找条件{int Mid = (L + R) / 2;if (a[Mid] == x)//查找到目标元素{ans = Mid;break;}if (a[Mid] < x) L = Mid + 1;else  R = Mid - 1;}return ans;
}int main()
{int n,x;cin >> n >> x;//以上图为例:8表示数组长度 4表示要查找的元素for (int i = 1;i <= n;i++) cin >> a[i];//输入数据1 3 4 6 10 20 21 22int ans = binarySearch(a,n,x);cout << ans << endl;//3return 0;
}

但是此处有一个小细节，那就是C++中的int有属于自己的取值范围，当L和R都很大时，(L + R) / 2可能会超出int的取值，从而导致出错(单独的L或者R可能不会超出int范围)。那么针对这个问题，如何改进呢？

二分查找冷笑话之时间复杂度

早晨，爱学习的wmy抱着一堆书进了阅览室，结果警报响了，大妈让wmy看看是哪本书把警报弄响了。wmy把书倒出来，准备—本一本的测。大妈见状急了，把书分成两份，第一份过了一下响了。又把这一份分成两份接着测，三回就找到了，大妈用鄙视的眼神看着wmy，仿佛在说O(n)和O(logn)都分不清。

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列 —— 选自百度百科

二分中的防越界问题以及改进方法

假设L = 1999999998，R = 1999999999，虽然L、R没有越界，但是一旦相加就会超过int范围导致计算出错

int mid=（L + R) / 2;//修改前

int mid = L + ( R - L) / 2;//修改后

L + ( R - L) / 2 = （L + R) / 2

思考题：

如果数组中有很多重复元素，那么需要完成以下问题，应该如何处理？

• 思考题1：如果要查找元素4的最小下标——3，该如何处理？
• 思考题2：如果要查找第一个大于4的元素下标——6，该如何处理？
• 思考题3：如果要统计元素4的个数，该如何处理？

lower_bound与upper_bound

lower_bound(first，last，val)函数返回一个非递减序列[first, last)中的第一个大于等于值val的地址

upper_bound(first，last，val)函数返回一个非递减序列[first, last)中的第一个大于值val的地址

思考题1 —— 答案：

只需要将二分模板改为：

int binarySearch(int a[],int n,int x)
{int L = 1,R = n;int ans = -1;while (L <= R){int Mid = L + (R - L) / 2;if (a[Mid] >= x){ans = Mid;R = Mid - 1;}else  L = Mid + 1;}return ans;
}

测试数据：
输入

9 4
1 2 2 3 4 4 4 4 22

输出

5

模板作用：用来查找数组中某个数x第一次出现的位置

思考题2 —— 答案：

只需要把上题模板中if语句内的>=号改为>即可

int binarySearch(int a[],int n,int x)
{int L = 1,R = n;int ans = -1;while (L <= R){int Mid = (L + R) / 2;if (a[Mid] > x){ans = Mid;R = Mid - 1;}else  L = Mid + 1;}return ans;
}

测试数据：

输入

9 4
1 2 2 3 4 4 4 4 22

输出

9

模板作用：用来查找数组中第一个值大于x的元素下标

练习：
Acwing 789 数的范围

作业题：A-B数对

作业题题解

方法一：暴力法

#include <iostream>using namespace std;const int N = 10010;
int a[N];int main()
{int n,c;cin >> n >> c;for (int i = 1;i <= n;i++) cin >> a[i];int ans = 0;for (int i = 1;i <= n;i++)for (int j = 1;j <= n;j++)if (a[i] - a[j] == c)ans ++;cout << ans << endl;return 0;
}

暴力法的缺点：题目中N表示整数的个数，而在说明中给出对于 100% 的数据，1 ≤ N ≤ 2 × 10 ^ 5 。暴力枚举所有的答案，时间复杂度为O(n ^ 2)，显然会超时。如图，但可以骗分

方法二：二分法
思路：题目要我们求出满足A - B = C的数对有多少个。但C是确定的，那么如果我们已知A，B就一定等于A - C。在这个思路里，我们只需要遍历一遍数组，然后寻找A - C的个数即可。
遍历数组的时间复杂度为O(n)，二分查找A - C的时间复杂度为O(logn)，故二分思路的时间复杂度为O(nlogn)

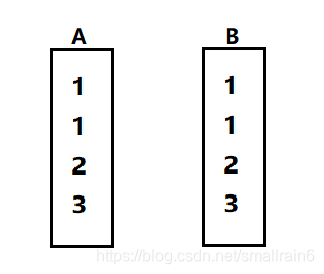
• 当A中A = 1时，C = 1(题目给出)，需要查找B中0的个数 —— 0
• 当A = 2时，C = 1，需要查找B中1的个数 —— 2
• 当A = 3时，C = 1，需要查找B中2的个数 —— 1
• 故答案为2 + 1 = 3

AC代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;
const int N = 2e5 + 10;
int nums[N];
LL ans;//注意long longint main()
{int n,c;cin >> n >> c;for (int i = 0;i < n;i++) cin >> nums[i];sort (nums,nums + n);//升序排列 -> 二分    for (int i = 0;i < n;i++){int a = nums[i];int b = a - c;int u = upper_bound(nums,nums + n,b) - nums;int l = lower_bound(nums,nums + n,b) - nums;ans += (u - l);}cout << ans << endl;return 0;
}

二分答案

例：2017年蓝桥杯A组真题 —— 分巧克力
问题描述：

儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。小明一共有N块巧克力，其中第i块是Hi x Wi的方格组成的长方形。为了公平起见，小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足：　　
1.形状是正方形，边长是整数
2.大小相同　　
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。当然小朋友们都希望得到的巧克力尽可能大，你能帮小Hi计算出最大的边长是多少么？

输入格式

第一行包含两个整数N和K。(1 <= N, K <= 100000)　　
以下N行每行包含两个整数Hi和Wi(1 <= Hi, Wi <= 100000)　　输入保证每位小朋友至少能获得一块1x1的巧克力。

输出格式·

输出切出的正方形巧克力最大可能的边长

样例输入

2 10
6 5
5 6

样例输出

2

AC代码

#include <iostream>using namespace std;const int N = 1e5 + 10;
int h[N],w[N];
int n,k;//n块巧克力,k个小朋友int getSum(int u)//当边长为u的时候可以得到多少块巧克力
{int sum = 0;//sum表示可以切出的巧克力总数for (int i = 0;i < n;i++) sum += (h[i] / u) * (w[i] / u);return sum;
}int main()
{cin >> n >> k;for (int i = 0;i < n;i++) cin >> h[i] >> w[i];//输入n块巧克力的边长int L = 1,R = 1e5;//二分答案(巧克力的边长最小是1,最大是1e5)while (L <= R)//执行二分的循环条件{int Mid = (R + L) / 2;//如果以Mid为边长得到的巧克力数可以给每个小朋友一块巧克力 —— getSum(Mid) >= k个小朋友//那么寻找是否有更大的边长 —— L = Mid + 1,即寻找是否还有最优解//否则,说明当前边长过大,需要减小当前的边长 —— R = Mid - 1if (getSum(Mid) >= k) L = Mid + 1;else R = Mid - 1;}cout << R << endl;return 0;
}

浮点二分

通过一个例题来介绍浮点二分

例1 求一个数的三次方根

原题链接

给定一个浮点数 n，求它的三次方根。

输入格式

共一行，包含一个浮点数 n。

输出格式

共一行，包含一个浮点数，表示问题的解。
注意，结果保留 6 位小数。

数据范围

−10000 ≤ n ≤ 10000

输入样例

1000.00

输出样例

10.000000

解题思路：
① 由于本题输入的数据范围是【−10000，10000】，显然，开三次根号之后答案的范围仍然在区间【−10000，10000】。

• 例如，将输入数据的范围设置为【-100，100】，输入数据是8，把8开三次根号是2，依旧在区间【-100，100】之内
• 再如，输入数据的范围为【-100，100】，输入数据是64，把64开三次根号是4，依旧在区间【-100，100】之内

② 本题的解法：浮点二分 + 二分答案

• 设置一个Mid，如果Mid ^ 3 >= n,说明当前的Mid还不是最优解，此时将右指针左移，即R = Mid.
  

• 同理，如果Mid ^ 3 <= n,说明当前的Mid也不是最优解，此时将左指针右移，即L = Mid.
  

• 反复执行以上步骤，直到L和R无限接近，就找到了答案

• 注意此处与整数二分的区别，在整数二分，更新区间的方法是使用L = Mid + 1砍掉左区间或R = Mid - 1砍掉右区间，在浮点二分中，对于精度的要求很高，直接把区间减1的话很可能就错过了答案

区分整数二分与浮点二分：

• 整数二分中，L' = Mid + 1或者R' = Mid - 1
• 在浮点二分中，L' = Mid或者R' = Mid

除了二分法，还有三分法，网上有很多资料，由于时间限制就不给大家讲解三分法了，留给大家自主学习

AC代码：

#include <iostream>
#include <cstdio>using namespace std;const double esp = 1e-8;//esp = 10 ^ (-8) ——无限趋近于0
double n;int main()
{cin >> n;double L = -10000,R = 10000;while (R - L > esp)//退出循环时,R - L小于无穷小,即L == R{double Mid = (L + R) / 2;if (Mid * Mid * Mid >= n) R = Mid;else L = Mid;}printf("%.6lf\n",L);//%.6lf表示保留小数点后6位return 0;
}

例2 剪绳子

原题链接

题目描述

有 N 根绳子，第 i 根绳子长度为 Li，现在需要 M 根等长的绳子，你可以对 N 根绳子进行任意裁剪（不能拼接），请你帮忙计算出这 M根绳子最长的长度是多少。

输入格式

第一行包含 2 个正整数 N、M，表示原始绳子的数量和需求绳子的数量。 第二行包含 N 个整数，其中第 i 个整数 Li 表示第 i
根绳子的长度。

输出格式

输出一个数字，表示裁剪后最长的长度，保留两位小数。

输入样例

3 4
3 5 4

输出样例

2.50

样例解释

第一根和第三根分别裁剪出一根 2.50 长度的绳子，第二根剪成 2 根 2.50 长度的绳子，刚好 4 根

解题思路： 浮点二分 + 二分答案

AC代码：

#include <iostream>
#include <cstdio>using namespace std;const int N = 1e5 + 10;//N表示绳子条数
int len[N];//原来存储n条绳子的长度int main()
{int n,m;cin >> n >> m;for (int i = 1;i <= n;i++) cin >> len[i];double L = 0,R = 1e9;double esp = 1e-4;while (R - L > esp){double Mid = (L + R) / 2;int ans = 0;//ans用来保存最后可以得到的等长绳子数量for (int i = 1;i <= n;i++)//遍历每根绳子的长度{int res = len[i] / Mid;ans += res;}if (ans >= m) L = Mid;//当前选择的绳子长度可以更大(ans = m时也可以尝试寻找是否有更大的解)else R = Mid;}printf("%.2lf\n",L);return 0;
}

总结“浮点二分+二分答案”的做法

• 第一步：明确题目最优解的范围在L=左区间和R=右区间中
• 第二步：while (R - L > eps) (其中eps为精度控制范围。经验：如果精度要求保留4位小数，那么eps一般设置为1e-6，如果精度要求保留6位小数，eps一般设置为1e-8)

    Mid = (L + R) / 2;if(A >= B)  L = Mid;//注意符号为大于等于,这样才可以使L和R无限接近else  R = Mid;

以上步骤执行完毕，那么L或R的值就是最终的答案