XGBOOST（Extreme Gradient Boosting）算法原理详细总结

        上篇我们对传统的GBDT算法原理进行了探讨，本篇我们来探讨一个具有王者地位的算法：XGBOOST（Extreme Gradient Boosting
）。XGBOOST是来自于华盛顿大学的一个研究项目，2016年由陈天奇和Carlos Guestrin在KDD上发表：XGBoost: A Scalable Tree Boosting System。自此之后，XGBOOST不仅在kaggle比赛中赢得一席之地，而且也推动了工业领域的一些前沿应用的发展。XGBOOST是我们处理中小型结构化数据必须要掌握的一个杀手锏。
        本篇我们主要参考陈天奇博士介绍XGBOOST的PPT：Boosted Trees 。

1）CART回归树

        CART回归树既可以处理分类任务又可以处理回归任务。CART算法对训练样本集的每个特征递归的进行二分判断，将特征空间划分为有限的单元，每个单元具有一定的权重。简单的可以认为，CART回归树是一个叶子节点具有权重的二叉决策树。CART回归树有两个特点：

• 决策规则和决策树是一样的；
• 决策树的每个叶子节点都包含一个权重；

下图就是一个回归决策树的示例：

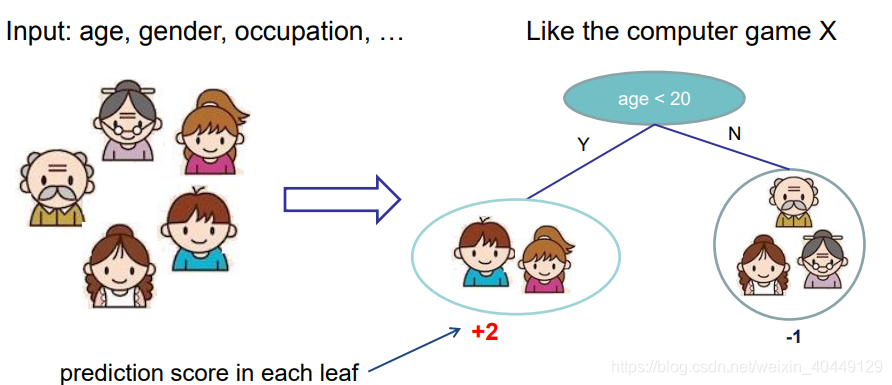
        假如某决策树的叶子节点数目为$T$，每个叶子节点的权重为 w → = { w 1 , w 2 , . . . w T } \overrightarrow{w}=\left\{w_1,w_2,...w_T\right\} w ={w1​,w2​,...wT​}，样本$x$落在叶节点$q$中，决策树模型$f(x)$可以定义为：
f t ( x ) = w q ( x ) w ∈ w → , q : R d → { 1 , 2 , . . . T } f_t(x) = w_{q(x)} \quad w \in \overrightarrow{w},q:R^d\rightarrow \left\{1,2,...T\right\} ft​(x)=wq(x)​w∈w ,q:Rd→{1,2,...T}
        从上式中可以看出，决策树的两个核心为：树的结构$q$，叶节点的权重$w$。确定树的结构和叶节点的权重便可以确定一颗决策树。
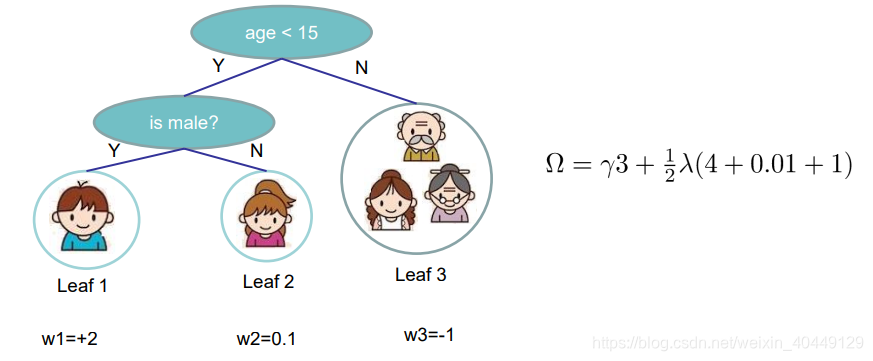
        在决策树算法原理中我们了解到，决策树比较容易过拟合，因此会对决策树进行剪枝操作。那么我们该如何衡量决策树的复杂度呢？我们可以使用，树的深度，叶节点数量，叶子节点权重的$L2$正则等。这里我们使用叶节点的数量和叶子节点权重的$L2$正则表示决策树模型的复杂度，数学表达式为：
$$\Omega (f_t)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
其中，$T$为叶节点的个数，$w$为叶节点所对应的权重，$\gamma$为收缩系数，$\lambda$为$L2$平滑系数。下图即为一个决策树模型复杂度的示例：

2）XGBOOST目标函数

        XGBOOST基于Boosting框架，它采用的是前向优化算法，即从前往后，逐渐建立基模型来优化逼近目标函数，具体过程如下：
${\hat{y}}_i^{(0)}=0$
${\hat{y}}_i^{(1)}=f_1(x_i)={\hat{y}}_i^{(0)}+f_1(x_i)$
${\hat{y}}_i^{(2)}=f_1(x_i)+f_2(x_i)={\hat{y}}_i^{(1)}+f_2(x_i)$
$...$
${\hat{y}}_i^{(t)}={\sum }_{k=1}^t{f}_k(x_i)={\hat{y}}_i^{(t-1)}+f_t(x_i)$
        从上式中，我们可以看出，每一步我们都是要训练一个新的基模型$f_t(x_i)$，那么我们的目标就是让训练的新模型使得误差最小，即目标函数为：
$$Ob{j}^{(t)}=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i)+\sum _{i=1}^t\Omega (f_i)$$
$$=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant$$
其中$\Omega (f_t)$为模型复杂度，用来防止模型过拟合，平衡模型偏差和方差的。
        由泰勒二阶展开式可知：
$$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\Delta x+\frac{1}{2}{f}^{\prime \prime }$$