【CS224n】笔记45 Word Window分类与神经网络和反向传播

这节课介绍了根据上下文预测单词分类的问题，推导了对权值矩阵和词向量的梯度，初步展示了深度学习与传统机器学习方法不一样的风格。

笔记概要

1、分类的一些主要符号
2、主要思想
2.1、机器学习角度的分类
2.2、基于softmax分类器的定义
2.3、softmax分类器损失函数定义
2.4、需要更新的参数
2.5、参数过多导致的过拟合&&正则化解决方式
2.6、softmax分类器损失函数最终定义
3、训练过程中是否应该重训练（retrain）词向量
4、基于window的词分类任务
4.1、基于window的分类器定义
4.2、 一个简单的基于window的softmax分类器
4.3、 基于window softmax分类器的求梯度过程
5、基于神经网络的词分类任务
5.1、神经网络的优势
5.2、神经网络的前向传播
5.3、NER2分类问题假设
5.4、神经网络的反向传播
6、总结
7、项目建议

1、分类的一些主要符号

说到分类任务，我们一般会有一个数据集包含样本：
xi：是一个 d维向量，表示输入，比如单词（序号或者向量），上下文窗口，句子，文档等等。
yi：是一个 C维one-hot向量，表示我们尝试预测的标签，比如分类：情感、命名实体、买卖决策；其他的单词；或者是多单词的句子。
N：总数。
{ x i , y i } i = 1 N \left \{ x_{i}, y_{i}\right\}_{i=1}^{N} {xi​,yi​}i=1N​

2、主要思想

2.1、机器学习角度的分类

如下图，从机器学习的角度来看：假设词向量x是固定的，仅仅更新的是逻辑回归的权重W，意味着仅仅修改的是决策边界。
下面是一个简单的通过逻辑回归的线性决策边界，对映射到二维空间的词向量进行分类的图例：

2.2、基于softmax分类器的定义

我们在训练集中xi,yi已知的情况下，通过学习逻辑回归的权重W得到决策边界。其中W代表权重矩阵，C代表分类标签的个数，d代表x的维度。
所以在W已知的情况下，对于每个输入x，他被分为yi标签的概率公式为：
$$p(y_i=1|x)=\frac{exp(W_j.x)}{{\sum }_{c=1}^{C}exp(W_c.x)}$$

$W_j.x$代表W的第j行与x列的点乘。
整个公式即：取权值矩阵的某一行乘上输入向量，归一化得到概率。最后会得到该输入x被分类为y1，y2，y3 …的概率，选取最大概率值即为它的类别。

点乘/内积 的几何意义是可以用来表征或计算两个向量之间的夹角，即相似度。注意：点乘的结果是一个标量(数量而不是向量)。
外积，又叫叉乘、叉积向量积：其运算结果是一个向量而不是一个标量。

2.3、softmax分类器损失函数定义

对于每一个样本，我们的目标是最大化xi 被正确分类成yi的概率，最大化上述公式等价于最小化该分类的负对数概率（一般都转化为最小化问题）：

接下来的问题是如何利用针对所有样本的所有可能分类的表达式表现出只针对正确分类的对数概率，这里主要引入了交叉熵（cross
entropy）的概念，其中P（c）表示一个分布，代表真实的样本是c类的概率，是一个one-hot向量，只有在c是正确分布的时候才取1，其他时候都取0；而q（c）表示的是我们在上面计算的softmax的概率，这样我们就利用一个针对所有可能的公式表示了正确分类的对数概率：

交叉熵（cross entropy）可以进一步进行化简，分为两个部分：

这其中的H（p）实际上公式是：

我们可以看到，这个H（p）是信息熵，DKL(p||q)KL散度是相对熵，交叉熵=信息熵+相对熵。
由于H（p）常常是一个常数，那么由上面这个公式我们可以知道，最小化交叉熵，实际上就是最小化DKL(p||q)。因此求这个式子的最小值等价于求第二项的最小值。
DKL(p||q)并不是一个距离，而是对两个概率分布(p和q)之差的非对称度量。

由以上描述我们可以得到对于整个训练集{xi,yi}，损失函数的形式如下，是一个平均交叉熵损失函数。

2.4、需要更新的参数

在一般的机器学习中，θ通常由W组成：

一般的ML问题中，参数由权值矩阵的列组成维度不会太大。而在词向量或其他深度学习中，需要同时学习权值矩阵和词向量。

上面公式里的θ就是权值矩阵所有参数（c⋅d）+词向量参数(|V|⋅d)，这里相比较传统分类问题，增加了词向量所有参数，这也是和传统分类问题的最大区别 。

2.5、参数过多导致的过拟合&&正则化解决方式

参数一多(特征，也就是权重矩阵w的行数)，就容易过拟合（如下图）：

由上图我们可以看出，模型复杂度越高，模型的训练集误差会越来越小；而随着模型复杂度的增高，测试集的误差会先减小后增大；这是因为模型太复杂时，模型变得过拟合。也就是说模型参数过度拟合了训练集的样本，时模型丧失了鲁棒性。所以在过拟合后，模型在训练集上效果会越来越好，在测试集上效果越来越差。

2.6、softmax分类器损失函数最终定义

因此，需要加入正则化项的损失函数，其作用其实就是降低模型参数的复杂度，防止过拟合。

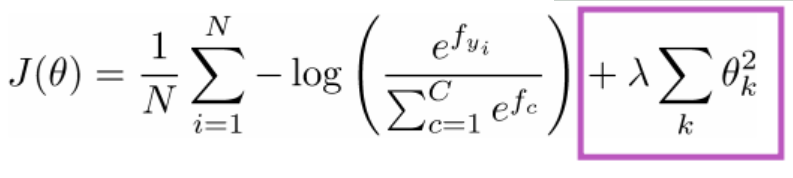
3、训练过程中是否应该重训练（retrain）词向量

对于一般的机器学习任务，我们只学习参数W，而不会retrain词向量（输入的词向量是什么就一直是什么）。那么如果我们在这个时候也retrain词向量会发生什么呢？

首先，下图是只学习参数W的分类器效果：

其中，TV、telly、televison三个单词会成功的划分到一起。

然后，下图是不仅仅学习决策边界W，还retrain词向量x的分类器效果：

由上图我们可以看到，当telly和TV都在训练集中时，retrain词向量后，telly和TV在空间中的位置都发生了变化；而televison没有在训练集中，所以television在空间中的位置没有变化。也这因为这个原因，television相对于telly和TV的位置发生了变化，在分类时发生了偏差。

根据以上我们可以总结出：
(1) 如果训练集的规模比较小，那我们就不要retrain词向量，否则会发生上图中效果。
(2) 如果我们有规模很大的数据集，那么retrain词向量会更遵循每个单词词向量在这个任务中的分布，从而使实验效果更理想。

4、基于window的词分类任务

4.1、基于window的分类器定义

上面都仅仅讨论了对于某个单词输入向量x，但目前仅仅分类单个单词的任务已经很少有人做了。现在更有趣的问题是根据上下文信息对单词进行语义消歧。
比如课程中提到的下面的两个例子：

由以上两个例子我们可知，根据单个单词分类已经不可能了；因为同样的单词，在不同的语境（上下文）中可能含有不同甚至相反的含义。此时基于窗口的词分类任务应运而生，这时候我们不仅仅用单一的单词，还用到他上下文的单词，共同决定这个中心词的类别。

4.2、 一个简单的基于window的softmax分类器

一个基于window的softmax分类器定义为：以待分类单词为中心词，取其周围某个窗口大小内的单词向量，将其进行拼接，构成分类器的输入；分类器的输出即为中心词的类别。
一个window大小为2，对Paris进行分类的例子：

其中，$X_{window}$∈$R^{5d}$ （5个单词，每个单词的词向量维度为d）

所以一个基于窗口的softmax分类器相当于以$X_{window}$为输入的softmax分类器（之前是以单个X向量作为输入）。softmax分类器前面叙述过了，其中平均交叉熵损失函数为：

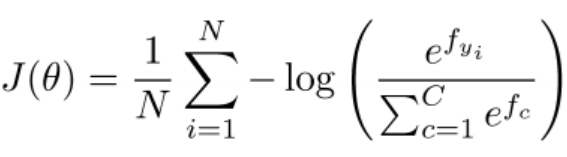
那么到此损失函数有了，我们怎么样训练这个分类器呢？

4.3、 基于window softmax分类器的求梯度过程

通过4.2我们得到了模型损失函数，那么接下来我们就以求一下对于词向量X求偏导得到的梯度（此部分假设retrain词向量）为例，权重矩阵W的梯度类似。

其中：$f_y=W_{y}x={\sum }_{i=1}^d{W}_{yi}xi$ ，fy表示第y个类别。如果y为预测正确的，则减去1（为什么？有点没懂）。
此时我们求出了词向量的梯度，更新词向量X的公式为梯度的负方向：$$X_{new}=X_{old}-\alpha \cdot {▽}_{X}J$$
其中，$\alpha$为学习率。

5、基于神经网络的词分类任务

5.1、神经网络的优势

对于少量的数据，softmax分类器这种通过线性分类边界进行分类的模型可能表现还不错，但是如果遇到复杂且大量的数据，这种简单的模型可能就很难拟合数据(而神经网络可以拟合任意非线性函数）。

5.2、神经网络的前向传播

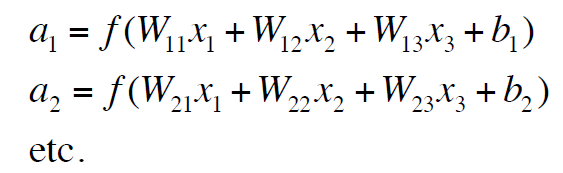
将上式表示成矩阵就是下面这样：

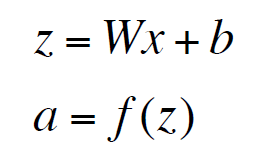
通过上式我们可以知道，如果我们不采用非线性的激活函数，输入经过两层神经网络后表示为W2W1X，最后还是WX，依然是线性变换。因此神经网络采用非线性函数（例如sigmod），能够更加拟合复杂的数据。

神经网络的最后一层我们可以计算一个通过softmax计算出来的概率值，也可以仅仅计算一个非规格化的分数（score）。

5.3、NER2分类问题假设

假设我们要预测中心词Paris是否是一个地名（即进行NER命名实体识别）的2分类问题：

输入层：$X$即为 $X_{window}$ 5个词拼接而成的窗口向量，每个词向量的维度di=4，则拼接后input 词向量的维度d=4X5=20；
隐藏层：隐藏层总共有8个神经元，因此全连接的话，有20X8个链接权重参数，用W表示。 f(x)为线性变换后的激活函数；
输出层：$u^T$为隐藏层到输出层之间的权重矩阵，s为输出得分值。

5.4、神经网络的反向传播

根据上面的分类任务，我们可以这样定义目标策略：最大化以Paris为中心词的窗口得分，最小化不是以Paris为中心词的得分，知道他们都足够好（类似word2vec中负采样）。为了遵循这个策略，我们将目标函数设置为最大间隔损失函数：

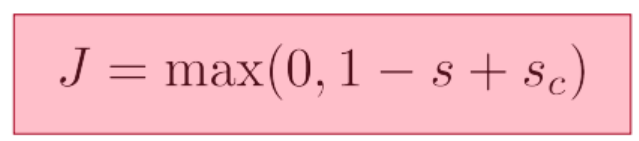
其中

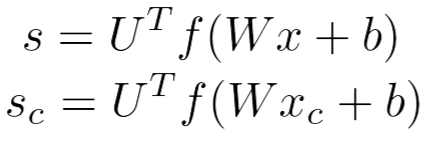
假设cost函数J>0（则Sc>S，需要继续优化），计算算S或者Sc的导数，涉及到的变量有W，U，b， x。

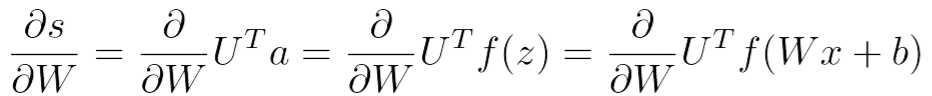
对权重矩阵W求偏导具体过程：
（就是链式求导过程）


其中：
如果激活函数是sigmod函数，则其导数如下（用原函数即可，不必再重新计算什么，极大减少了运算量）：

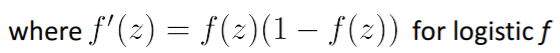
上面是对单个数据进行的梯度计算，如果我们想求整个权重矩阵的梯度，则转化成矩阵形式（矩阵即简便表达，又能极大的提升运算速度）：

那么怎么更新bias b呢？

其实就是上上式子最后一步不对W求偏导了，而是对b求，那么（WX+b）对b的倒数为1，则为δi。

由此可见，反向传播最精髓的地方就是记住链式求导法则。
附上一个连接：用实例进行前向和反向传播演示

课中所提重要技巧！！

我们可以重复使用在高层计算的导数来计算低层的导数！

因为很多值是被重复计算的，这是一个很有效的技巧，极大的提升了效率。
【为什么用反向传播：我们可以重复使用这些误差信号δ和元素的导数。】

6、总结

对于每一个窗口来说，都有以下目标函数：
如果J>0，则2分类中label为1，否则为0。（这里不知道理解的对不对）

7、项目建议

(1) 先定义好自己的问题，明确知己的目标是做什么。
(2) 根据自己的问题，确定实验所需数据集，可以用现成前人发布的数据集，也可以自己用爬虫在网络上爬取（不建议在爬取数据上花费大量的精力）。
(3) 确定自己实验结果的评价标注。比如机器翻译常用BLEU值；一般用准确率、召回率、F1值。根据数据特点和任务的不同采用不同的评价标准。
(4) 正确的将自己的数据划分成训练集、验证集和测试集。
(5) 可以先采用一些简单的、比较基础的模型完成目标，然后分析输出结果，适当调整和改变模型
(6) 将实验数据可视化，也可以将实验过程可视化，通过图表可以很明确的了解自己模型对于超参数不同大小的敏感度。
(7) 尝试改进或者混合模型，得到更好的实验效果。