本文主要是介绍ACM第六次比赛题目及标准程序(动态规划),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
欢迎访问XYNUOJ
问题A:多项式求和
时间限制: 1 Sec 内存限制: 32 MB题目描述
多项式的描述如下:
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ...
现在请你求出该多项式的前n项的和。
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ...
现在请你求出该多项式的前n项的和。
输入
输入数据由2行组成,首先是一个正整数m(m<100),表示测试实例的个数,第二行包含m个正整数,对于每一个整数(不妨设为n,n<1000),求该多项式的前n项的和。
输出
对于每个测试实例n,要求输出多项式前n项的和。每个测试实例的输出占一行,结果保留2位小数。
样例输入
2
1 2
样例输出
1.00
0.50
#includeint main()
{
//预处理最舒服,时间复杂度为O(1)
double ans[1005];//不用纠结用float还是double,一步到位用精度更高的double。
double m=1,temp=1,cnt=2;
ans[1]=1;
for(int i=2;i<1000;i++)
{
temp=m/cnt;
if(i%2)//奇数
{
ans[i]=ans[i-1]+temp;
}
else
{
ans[i]=ans[i-1]-temp;
}
cnt++;
}
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("%0.2lf\n",ans[n]);
}
return 0;
}
#includeint main()
{
//预处理最舒服,时间复杂度为O(1)
double ans[1005];//不用纠结用float还是double,一步到位用精度更高的double。
double m=1,temp=1,cnt=2;
ans[1]=1;
for(int i=2;i<1000;i++)
{
temp=m/cnt;
if(i%2)//奇数
{
ans[i]=ans[i-1]+temp;
}
else
{
ans[i]=ans[i-1]-temp;
}
cnt++;
}
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("%0.2lf\n",ans[n]);
}
return 0;
}问题B: Fibonacci Again
时间限制: 1 Sec 内存限制: 16 MB题目描述
There are another kind of Fibonacci numbers: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2).
输入
Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000).
输出
Print the word "yes" if 3 divide evenly into F(n).
Print the word "no" if not
样例输入
0
1
2
3
4
5 样例输出
no
no
yes
no
no
no
#includeint a[1000005];
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
a[0]=1;
a[1]=2;
if(n<2)
printf("no\n");//简单题要注意特殊数据。
else
{
for(int i=2;i<=n;i++)
{
a[i]=(a[i-1]+a[i-2])%3;
}
if(a[n]%3==0)
printf("yes\n");
else
printf("no\n");
}
}
return 0;
}
#includeint a[1000005];
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
a[0]=1;
a[1]=2;
if(n<2)
printf("no\n");//简单题要注意特殊数据。
else
{
for(int i=2;i<=n;i++)
{
a[i]=(a[i-1]+a[i-2])%3;
}
if(a[n]%3==0)
printf("yes\n");
else
printf("no\n");
}
}
return 0;
}问题C: A^B
时间限制: 1 Sec 内存限制: 32 MB题目描述
求A^B的最后三位数表示的整数。
说明:A^B的含义是“A的B次方”
说明:A^B的含义是“A的B次方”
输入
输入数据包含多个测试实例,每个实例占一行,由两个正整数A和B组成(1<=A,B<=10000),如果A=0, B=0,则表示输入数据的结束,不做处理。
输出
对于每个测试实例,请输出A^B的最后三位表示的整数,每个输出占一行。
样例输入
2 3
12 6
6789 10000
0 0 样例输出
8
984
1 #include//和B题类似 都是取余
int main()
{
int m,n;
while(scanf("%d%d",&m,&n)!=EOF&&m&&n)
{
int ans=1;
for(int i=0;i
#include//和B题类似 都是取余
int main()
{
int m,n;
while(scanf("%d%d",&m,&n)!=EOF&&m&&n)
{
int ans=1;
for(int i=0;i 问题D: How Many Tables
时间限制: 1 Sec 内存限制: 128 MB
题目描述
Today is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
输入
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
输出
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
样例输入
2
5 3
1 2
2 3
4 55 1
2 5 样例输出
2
4 #include#includeint pre[1080];
//并查集模板题
int Find(int x)//找老板
{
int r=x;
while(r!=pre[r])
r=pre[r];
return r;
}
void merge(int x,int y)//联合
{
int fx=Find(x),fy=Find(y);
if(fx!=fy)
pre[fy]=fx;
}
int main()
{
int casenum;
scanf("%d",&casenum);
while(casenum--)
{
int N,M,a,b,i,j,ans;
scanf("%d%d",&N,&M);
for(i=1;i<=N;i++)//初始化i的父结点为其本身
pre[i]=i;
for(i=1;i<=M;i++)//吸收并整理
{
scanf("%d%d",&a,&b);
merge(a,b);
}
for(ans=0,i=1;i<=N;i++)
if(pre[i]==i)
ans++;//判断有几个独立块
printf("%d\n",ans);
}
return 0;
}
问题E:爱旅游的小明
时间限制: 1 Sec 内存限制: 128 MB
题目描述
小明想去旅游,但是交通地图上的路太多了。路多了也不好,每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。这让小明很困扰。
现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。
输入
本题目包含多组数据,请处理到文件结束。
每组数据第一行包含两个正整数N和M(0<N<200,0<M<1000),分别代表现有城镇的数目和已修建的道路的数目。城镇分别以0~N-1编号。
接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B<N,A!=B,0<X<10000),表示城镇A和城镇B之间有一条长度为X的双向道路。
再接下一行有两个整数S,T(0<=S,T<N),分别代表起点和终点。
输出
对于每组数据,请在一行里输出小明最短需要行走的距离。如果不存在从S到T的路线,就输出-1.
样例输入
3 3
0 1 1
0 2 3
1 2 1
0 2
3 1
0 1 1
1 2 样例输出
2
-1 #include#include#includeusing namespace std;
const int INF=0x3f3f3f3f;
const int N=210;
int n,m,cnt;
int dis[N];
struct node{
int u,v,w;
}edge[1010*2];
void addedge(int u,int v,int w)
{
edge[cnt].u=u; edge[cnt].v=v; edge[cnt].w=w;
cnt++;
edge[cnt].u=v; edge[cnt].v=u; edge[cnt].w=w;
cnt++;
}
int Bellman_Ford(int src,int des)
{
int i,k;
for(i=0;i到某边终点的距离加上这条边的长度
if(dis[edge[i].u]!=INF && dis[edge[i].v]>dis[edge[i].u]+edge[i].w)
dis[edge[i].v]=dis[edge[i].u]+edge[i].w;
return dis[des]==INF?-1:dis[des];
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
cnt=0;
int u,v,w;
for(int i=0;i#include #include using namespace std; //4种解法 比较简单的是Dijkstra和Floyd。另外两种相对更难理解 const int INF=0x3f3f3f3f; const int N=210; int n,m,s,t; int map[N][N],dis[N],vis[N]; void Dijkstra(int src) { int i,j,k,tmp; for(i=0;i dis[j]) k=j,tmp=dis[j]; if(tmp==INF) break; vis[k]=1; for(j=0;j dis[k]+map[k][j]) dis[j]=dis[k]+map[k][j]; } } int main() { while(~scanf("%d%d",&n,&m)) { int u,v,w; for(int i=0;i w) map[u][v]=map[v][u]=w; } scanf("%d%d",&s,&t); Dijkstra(s);//计算从点s到其他所有点的距离 if(dis[t]==INF) printf("-1\n"); else printf("%d\n",dis[t]); } return 0; }#include #include #include #include using namespace std; const int INF=0x3f3f3f3f; const int N=210; int n,m,i,j,k,map[N][N]; //Floyd算法可能是最容易理解的,但是有利有弊。 //遇到稍微严格数据,超时的可能性非常大。毕竟3个for循环嵌套 void Floyd() { for(k=0;k map[i][k]+map[k][j]) map[i][j]=map[i][k]+map[k][j]; } int main() { while(~scanf("%d%d",&n,&m)) { for(i=0;i w) map[u][v]=map[v][u]=w; } int s,t; scanf("%d%d",&s,&t); Floyd(); if(map[s][t]==INF) printf("-1\n"); else printf("%d\n",map[s][t]); } return 0; }#include #include #include using namespace std; #define N 205 #define INF 99999999 int n,m,map[N][N]; int visited[N],dis[N]; int SPFA(int src,int des) { int i; for(i=0;i myqueue; while(!myqueue.empty()) myqueue.pop(); dis[src]=0; visited[src]=1; myqueue.push(src); int tmp; while(!myqueue.empty()) { tmp=myqueue.front(); myqueue.pop(); visited[tmp]=0; for(i=0;i dis[tmp]+map[tmp][i]) { dis[i]=dis[tmp]+map[tmp][i]; if(!visited[i]) { visited[i]=1; myqueue.push(i); } } } } return dis[des]; } int main() { int u,v,cost; while(scanf("%d%d",&n,&m)!=EOF) { int i,j; for(i=0;i
问题F: Is It A Tree?
时间限制: 1 Sec 内存限制: 128 MB
题目描述
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
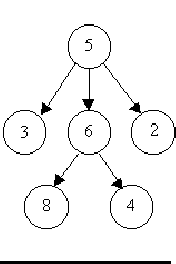
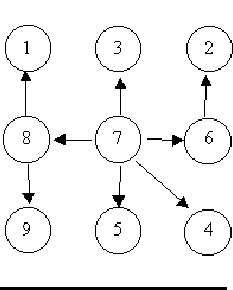
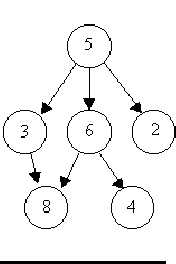
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
输入
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero .
输出
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
样例输入
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1 样例输出
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree. /*
树的三个条件
1,无环
2,除了根,所有的入度为1,根入度为0
3,只有一个根,
注意:空树也是树,只有根. 不过在此题中因为输入格式限制.所以不用考虑空树
*/
#includeconst int max_num=100010;
typedef struct
{
int num,root,conn;//数据,根结点,入度
}Node;
Node node[max_num];
void init()//初始化
{
for(int i=0;i=0&&m>=0)
{
if(!flag&&n!=0&&m!=0)continue;//判断是否是树
if(n==0&&m==0)//说明输入结束,开始处理吧
{
int root_num=0;
for(int j=1;j1)//如果出现某个节点的入度超过1,则不是树
{
flag=false;
break;
}
}
if(root_num>1)//连通分支大于1,是森林,不是树
flag=false;
if(flag)
printf("Case %d is a tree.\n",i++);
else printf("Case %d is not a tree.\n",i++);
init();//为下一个case处理进行初始化
continue;
}
if(m!=n&&find(n)==find(m)||m==n)
flag=false;
else
{
//将m,n记为结点
node[m].num=1;
node[n].num=1;
node[m].conn++;//入度加一
merge(n,m);
}
}
return 0;
}
问题 G: 确定比赛名次
时间限制: 1 Sec 内存限制: 128 MB
题目描述
有N个比赛队(1<=N<=500),编号依次为1,2,3,。。。。,N进行比赛,比赛结束后,裁判委员会要将所有参赛队伍从前往后依次排名,但现在裁判委员会不能直接获得每个队的比赛成绩,只知道每场比赛的结果,即P1赢P2,用P1,P2表示,排名时P1在P2之前。现在请你编程序确定排名。 输入
输入有若干组,每组中的第一行为二个数N(1<=N<=500),M;其中N表示队伍的个数,M表示接着有M行的输入数据。接下来的M行数据中,每行也有两个整数P1,P2表示即P1队赢了P2队 。
输出
给出一个符合要求的排名。输出时队伍号之间有空格,最后一名后面没有空格。
其他说明:符合条件的排名可能不是唯一的,此时要求输出时编号小的队伍在前;输入数据保证是正确的,即输入数据确保一定能有一个符合要求的排名。
样例输入
4 3
1 2
2 3
4 3 样例输出
1 2 4 3 /*
下一模块的动态规划经典题
先对n中物品的重量排序
dp[i][j]表示前i个物品中选j对的最小疲劳度。
则dp[i][j]可能含有第i个物品(这种情况下,第i种物品一定是和第i-1个物品配对),
则dp[i][j]=dp[i-2][j-1]+(val[i]-val[i-1])*(val[i]-val[i-1])
dp[i][j]的j对也可能不含有第i个物品,此时有dp[i][j]=dp[i-1][j]
状态转移方程:
dp[i][j]=min{dp[i-2][j-1]+(val[i]-val[i-1])*(val[i]-val[i-1]),dp[i-1][j]
*/
#include#include#define size 2005
#define INIT 2147483646//2^31-1
int cmp(const void *a,const void *b)//降序排序
{
return *(int *)a-*(int *)b;
}
int Min(int a,int b)//大小比较
{
return a
问题 H: 搬寝室
时间限制: 1 Sec 内存限制: 128 MB
题目描述
搬寝室是很累的,小明深有体会.那天小明迫于无奈要从4号楼搬到5号楼,因为4号要封楼了.看着寝室里的n件物品,小明开始发呆,因为n是一个小于2000的整数,实在是太多了,于是小明决定随便搬2*k件过去就行了.但还是会很累,因为2*k也不小是一个不大于n的整数.幸运的是小明根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如小明左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的小明希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度),请告诉他吧.
输入
每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数).
输出
对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行.
样例输入
2 1
1 3 样例输出
4 /*
下一模块的动态规划经典题
先对n中物品的重量排序
dp[i][j]表示前i个物品中选j对的最小疲劳度。
则dp[i][j]可能含有第i个物品(这种情况下,第i种物品一定是和第i-1个物品配对),
则dp[i][j]=dp[i-2][j-1]+(val[i]-val[i-1])*(val[i]-val[i-1])
dp[i][j]的j对也可能不含有第i个物品,此时有dp[i][j]=dp[i-1][j]
状态转移方程:
dp[i][j]=min{dp[i-2][j-1]+(val[i]-val[i-1])*(val[i]-val[i-1]),dp[i-1][j]
*/
#include#include#define size 2005
#define INIT 2147483646//2^31-1
int cmp(const void *a,const void *b)//降序排序
{
return *(int *)a-*(int *)b;
}
int Min(int a,int b)//大小比较
{
return a
这篇关于ACM第六次比赛题目及标准程序(动态规划)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






