本文主要是介绍运筹学 二、单纯形法(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、思路:从线性方程组中找出一个个的单纯形,每一个单纯形可以求得一组解,然后再判断该解使目标函数值是增大还是变小,决定下一步选择的单纯形。这就是迭代,直到目标函数实现最大值或最小值为止。最终得到最优解。
2、例:
![]()

系数矩阵可以写成:
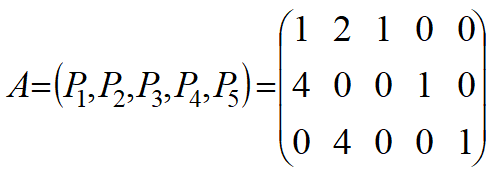
我们可以发现以x3,x4,x5的系数可以构成单位矩阵,我们可以以x3,x4,x5为基变量,可以化成:
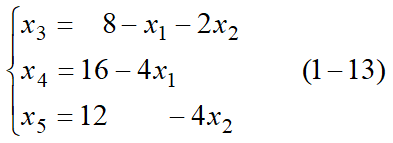
使非基变量x1=0,x2=0
可以得出,
![]()
我们此时可以得到一个基解:X(0)=(0,0,8,16,12)T
只要在目标函数的表达式中还存在有正系数的非基变量,这表示目标函数值还有增加的可能,就需要将非基变量与基变量进行对换。
x2与x5进行变换,


以此类推,求得X(2)=(2,3,0,8,0)T,X(3)=(4,2,0,0,4)T
z=14−1.5x3− 0.125x4
这篇关于运筹学 二、单纯形法(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!