阿白数模笔记之粒子群法(Particle Swarm Optimization，PSO)负反馈（Degenerative Feedback）修正及MATLAB代码详解

目录

Preface

基本粒子群法（Basic particle swarm optimization）

负反馈（Degenerative Feedback）修正

MATLAB代码详解

多峰函数

 参数初始化

迭代过程

结果显示

参考文章

Preface

        粒子群优化（Particle Swarm Optimization, PSO），又称微粒群算法，是由J. Kennedy和R. C. Eberhart等于1995年开发的一种演化计算技术，来源于对一个简化社会模型的模拟。其中“群（swarm）”来源于微粒群匹配M. M. Millonas在开发应用于人工生命（artificial life）的模型时所提出的群体智能的5个基本原则。“粒子（particle）”是一个折衷的选择，因为既需要将群体中的成员描述为没有质量、没有体积的，同时也需要描述它的速度和加速状态。

基本粒子群法（Basic particle swarm optimization）

        在D维空间，N个粒子组成一个群落，每个粒子位置坐标是D维向量，

，在每个维度上的速度也是D维向量，在迭代过程中，对每一个粒子，保留它迄今为止搜索到的最优位置为个体极值，整个粒子群搜索到的最优路径为，每进行一次迭代，粒子的位置和速度都会更新，更新公式为

,i表示第几个粒子，j表示维度

其中w是惯性系数，即前一次迭代速度对后一次的影响系数，表示个体目前最优极值对搜索的影响，反映了粒子的认知能力，，表示群体最优极值对个体的影响，反映了粒子的社会性行为，,均为正反馈调节。

负反馈（Degenerative Feedback）修正

        在速度更新公式的基础上，引入负反馈调节因子进行修正。在迭代过程中，对每一个粒子迄今为止搜索到的最差路径为个体极差值，，整个粒子群搜索到的最优路径为，修正后的速度更新公式为，其中

，表示负反馈调节，增强了个体的认知能力的社会能力。

MATLAB代码详解

多峰函数

        这是待求极小值的多峰函数

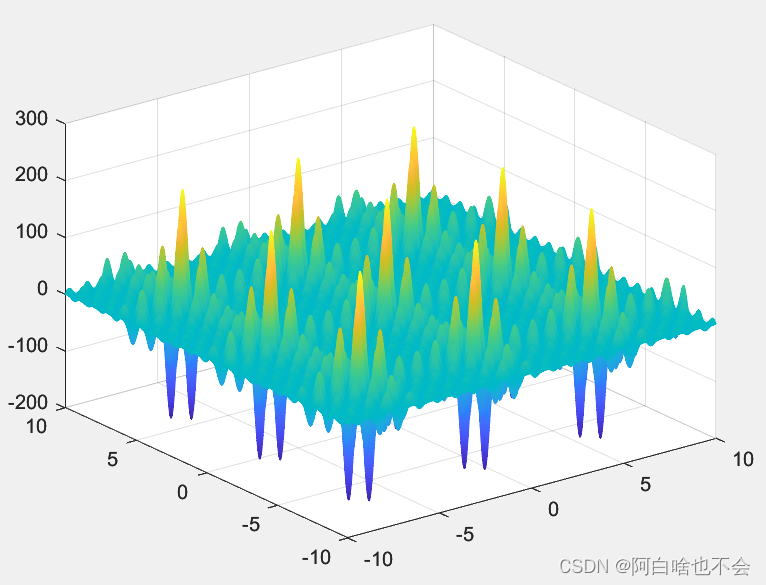
function v=func3(x)
v=((1*cos((1+1).*x(1)+1))+(2*cos((2+1).*x(1)+2))+(3*cos((3+1).*x(1)+3))+...(4*cos((4+1).*x(1)+4))+(5*cos((5+1).*x(1)+5))).*((1*cos((1+1).*x(2)+1))+...(2*cos((2+1).*x(2)+2))+(3*cos((3+1).*x(2)+3))+(4*cos((4+1).*x(2)+4))+(5*cos((5+1).*x(2)+5)));
end

x=linspace(-10,10,2000);
y=x;
z=meshgrid(x,y);
for i=1:size(x,2)for j=1:size(x,2)z(i,j)=func3([x(i),y(j)]);end
end
mesh(x,y,z);

 参数初始化

clear all; %清除所有变量
close all; %清图
clc; %清屏
N = 100; %群体粒子个数
D = 2; %粒子维数
T = 200; %最大迭代次数
c1 = 1.5; %正反馈调节因子1
c2 = 1.5; %正反馈调节因子2
c3=-0.5;%负反馈调节因子1
c4=-0.5;%负反馈调节因子2
Wmax = 0.8; %惯性权重最大值
Wmin = 0.4; %惯性权重最小值
Xmax = 10; %位置最大值
Xmin = -10; %位置最小值
Vmax = 1; %速度最大值，当更新后速度v>Vmax，取v=Vmax
Vmin = -1; %速度最小值,当更新后速度v<Vmin,取v=Vmin

%%%%%%%%%%%%初始化种群个体(限定位置和速度)%%%%%%%%%%%%
x = rand(N,D) * (Xmax-Xmin)+Xmin;
v = rand(N,D) * (Vmax-Vmin)+Vmin;%%%%%%%%%%%%%初始化个体最优位置最优值以及最差位置最差值%%%%%%%%%%%%%
p = x;
pw=x;
pbest = ones(N,1);
for i = 1:Npbest(i) = func3(x(i,:));
end
pworst=pbest;%初始时刻个体最优值也是最差值%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%
g = ones(1,D);
gw=ones(1,D);
gbest = inf;
gworst=-inf;
for i = 1:Nif(pbest(i) < gbest)g = p(i,:);gbest = pbest(i);elseif (pbest(i)>gworst)gw=p(i,:);gworst=pbest(i);end
end
gb = ones(1,T);%记录每次迭代最优值

迭代过程

%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%
for i = 1:Tfor j = 1:N%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%if (func3(x(j,:)) < pbest(j))p(j,:) = x(j,:);pbest(j) = func3(x(j,:));%%%%%%%%%更新个体最差位置和最差值%%%%%%%%%%%%%elseif (func3(x(j,:)) >pworst(j))pw(j,:)=x(j,:);pworst(j)= func3(x(j,:));end%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%if(pbest(j) < gbest)g = p(j,:);gbest = pbest(j);%%%%%%%%%%更新最差位置和最差值%%%%%%%%%%%%elseif (pworst(j) > gworst)gw=p(j,:);gworst=pworst(j);end%%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%%%w = Wmax-(Wmax-Wmin)*i/T;%线性递减公式%%%%%%%%%%%%更新位置和速度值%%%%%%%%%%%%%%%v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...+c2*rand*(g-x(j,:))+c3*rand*(pw(j,:)-x(j,:))+c4*rand*(gw-x(j,:));x(j,:) = x(j,:)+v(j,:);%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%for ii = 1:Dif (v(j,ii) > Vmax) | (v(j,ii) < Vmin)v(j,ii) = rand * (Vmax-Vmin)+Vmin;endif (x(j,ii) > Xmax) | (x(j,ii) < Xmin)x(j,ii) = rand * (Xmax-Xmin)+Xmin;endendend%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%gb(i) = gbest;
end

结果显示

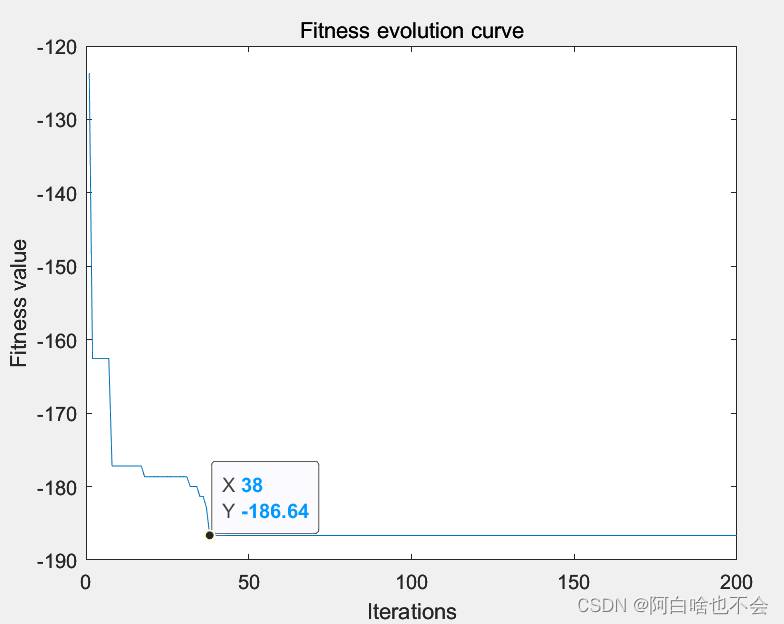
g  %最优个体
gb(end)  %最优值
figure
plot(gb)
xlabel('Iterations');
ylabel('Fitness value');
title('Fitness evolution curve')

参考文章

基本粒子群算法小结及算法实例（附Matlab代码）