混合专家模型 Mixture-of-Experts (MoE)

本文主要是介绍混合专家模型 Mixture-of-Experts (MoE)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

大纲

• Mixture-of-Experts (MoE)
• Mixture of Sequential Experts（MoSE）
• Multi-gate Mixture-of-Experts (MMoE)

一、MoE

1. MoE架构

MoE（Mixture of Experts）层包含一个门网络（Gating Network）和n个专家网络（Expert Network）。对于每一个输入，动态地由门网络选择k个专家网络进行激活。在具体设计中，每个输入x激活的专家网络数量k往往是一个非常小的数字。比如在MoE论文的一些实验中，作者采用了n=512，k=2的设定，也就是每次只会从512个专家网络中挑选两个来激活。在模型运算量（FLOPs）基本不变的情况下，可以显著增加模型的参数量。

MoE架构的主要特点是在模型中引入了专家网络层，通过路由机制(Routing function)选择激活哪些专家，以允许不同的专家模型对输入进行独立处理，并通过加权组合它们的输出来生成最终的预测结果。

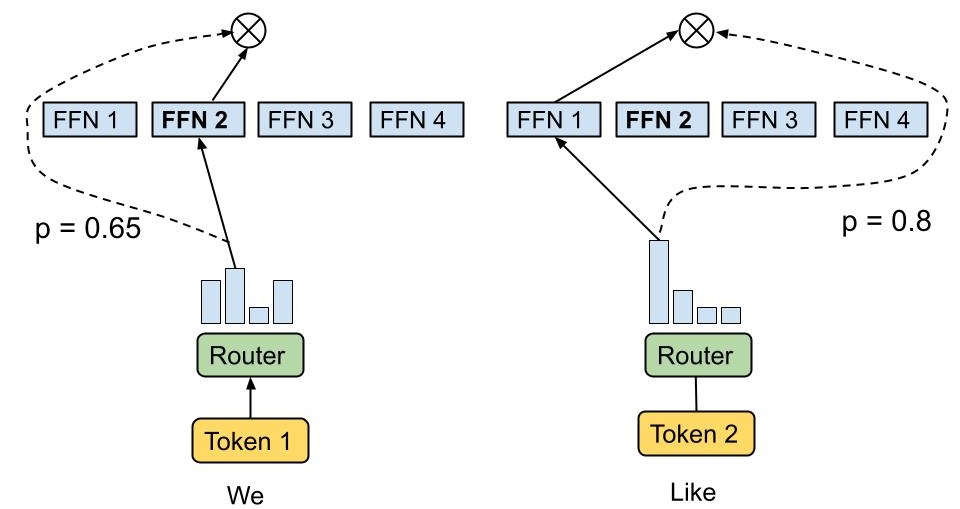
通过稀疏模型MoE扩大大语言模型的方法：以GLaM模型为例，它包含1.2T个参数，但实际上被激活的参数（activated parameters）只有97B，远少于GPT-3，也就是说，它是稀疏激活的MoE。它与GPT-3同样是只有解码器的模型，但与GPT-3相比，GlaM获得了更好的性能。

稀疏模型的优势在于它能够更有效地利用模型参数，减少不必要的计算开销，从而提高模型的性能。

1. 可以扩大模型的参数数量，因为只需要激活部分参数，其他参数可以被"关机"。这降低了计算量和内存消耗。
2. 提高效率：只激活相关的专家模块，可以提高模型效率。
3. 组合优势：通过组合不同专家的优势，有可能获得更好的效果。

混合专家系统有两种架构：competitive MoE 和cooperative MoE。competitive MoE中数据的局部区域被强制集中在数据的各离散空间，而cooperative MoE没有进行强制限制。

2. GateNet：决策输入样本由哪个专家处理

GateNet可以理解为一个分配器，根据输入样本的特征，动态决策将其分配给哪个专家进行处理。这个过程可以通过一个softmax分类器来实现，其中每个神经元对应一个专家模型。GateNet的输出值表示了每个专家的权重。 GateNet的设计需要考虑两个关键点：输入样本特征的提取和分配策略的确定。在特征的提取方面，常用的方法是使用卷积神经网络（CNN）或者Transformer等结构来提取输入样本的特征表示。而在分配策略的确定方面，可以采用不同的注意力机制或者引入一些先验知识来指导。

这种训练过程传统上是使用期望最大化 (Expectation Maximization, EM) 来实现的。门控网络可能有一个 softmax 输出，它为每个专家提供类似概率的置信度分数。

对softmax做了一些改动。第一个变动就是KeepTopK，这是个离散函数，将top-k之外的值强制设为负无穷大，从而softmax后的值为0。第二个变动是加了noise，这个的目的是为了做均衡，这里引入了一个Wnoise的参数，后面还会在损失函数层面进行改动。

上述公式表示了包含 n 个专家的 MoE 层的计算过程。具体来讲，首先对样本 x 进行门控计算， W 表示权重矩阵；然后由 Softmax 处理后获得样本 x 被分配到各个 expert 的权重； 然后只取前 k (通常取 1 或者 2）个最大权重，最终整个 MoE Layer 的计算结果就是选中的 k 个专家网络输出的加权和。

3. Experts：专家模型的构建与训练

专家模型是MoE架构中的核心组件，它们负责处理输入样本的具体任务。每个专家模型都是相对独立的，可以根据任务的需求选择不同的模型架构。 在训练阶段，专家模型可以采用传统的有监督学习方法进行训练。然而，为了提高模型的效果，还可以引入一些主从式训练策略。即通过联合训练GateNet和Experts，共同优化整个MoE架构。

为了改进只有几个expert会被集中使用这一问题，给每个expert定义了一个importance的概念。importance就是指这个expert所处理的样本数，简而言之就是G(x)对应位置的和。损失函数则是importance的平方乘以一个系数。

4. 代码实现

# Sparsely-Gated Mixture-of-Experts Layers.
# See "Outrageously Large Neural Networks"
# https://arxiv.org/abs/1701.06538
#
# Author: David Rau
#
# The code is based on the TensorFlow implementation:
# https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/expert_utils.pyimport torch
import torch.nn as nn
from torch.distributions.normal import Normal
import numpy as npclass SparseDispatcher(object):"""Helper for implementing a mixture of experts.The purpose of this class is to create input minibatches for theexperts and to combine the results of the experts to form a unifiedoutput tensor.There are two functions:dispatch - take an input Tensor and create input Tensors for each expert.combine - take output Tensors from each expert and form a combined outputTensor.  Outputs from different experts for the same batch element aresummed together, weighted by the provided "gates".The class is initialized with a "gates" Tensor, which specifies whichbatch elements go to which experts, and the weights to use when combiningthe outputs.  Batch element b is sent to expert e iff gates[b, e] != 0.The inputs and outputs are all two-dimensional [batch, depth].Caller is responsible for collapsing additional dimensions prior tocalling this class and reshaping the output to the original shape.See common_layers.reshape_like().Example use:gates: a float32 `Tensor` with shape `[batch_size, num_experts]`inputs: a float32 `Tensor` with shape `[batch_size, input_size]`experts: a list of length `num_experts` containing sub-networks.dispatcher = SparseDispatcher(num_experts, gates)expert_inputs = dispatcher.dispatch(inputs)expert_outputs = [experts[i](expert_inputs[i]) for i in range(num_experts)]outputs = dispatcher.combine(expert_outputs)The preceding code sets the output for a particular example b to:output[b] = Sum_i(gates[b, i] * experts[i](inputs[b]))This class takes advantage of sparsity in the gate matrix by including in the`Tensor`s for expert i only the batch elements for which `gates[b, i] > 0`."""def __init__(self, num_experts, gates):"""Create a SparseDispatcher."""self._gates = gatesself._num_experts = num_experts# sort expertssorted_experts, index_sorted_experts = torch.nonzero(gates).sort(0)# drop indices_, self._expert_index = sorted_experts.split(1, dim=1)# get according batch index for each expertself._batch_index = torch.nonzero(gates)[index_sorted_experts[:, 1], 0]# calculate num samples that each expert getsself._part_sizes = (gates > 0).sum(0).tolist()# expand gates to match with self._batch_indexgates_exp = gates[self._batch_index.flatten()]self._nonzero_gates = torch.gather(gates_exp, 1, self._expert_index)def dispatch(self, inp):"""Create one input Tensor for each expert.The `Tensor` for a expert `i` contains the slices of `inp` correspondingto the batch elements `b` where `gates[b, i] > 0`.Args:inp: a `Tensor` of shape "[batch_size, <extra_input_dims>]`Returns:a list of `num_experts` `Tensor`s with shapes`[expert_batch_size_i, <extra_input_dims>]`."""# assigns samples to experts whose gate is nonzero# expand according to batch index so we can just split by _part_sizesinp_exp = inp[self._batch_index].squeeze(1)return torch.split(inp_exp, self._part_sizes, dim=0)def combine(self, expert_out, multiply_by_gates=True):"""Sum together the expert output, weighted by the gates.The slice corresponding to a particular batch element `b` is computedas the sum over all experts `i` of the expert output, weighted by thecorresponding gate values.  If `multiply_by_gates` is set to False, thegate values are ignored.Args:expert_out: a list of `num_experts` `Tensor`s, each with shape`[expert_batch_size_i, <extra_output_dims>]`.multiply_by_gates: a booleanReturns:a `Tensor` with shape `[batch_size, <extra_output_dims>]`."""# apply exp to expert outputs, so we are not longer in log spacestitched = torch.cat(expert_out, 0).exp()if multiply_by_gates:stitched = stitched.mul(self._nonzero_gates)zeros = torch.zeros(self._gates.size(0), expert_out[-1].size(1), requires_grad=True, device=stitched.device)# combine samples that have been processed by the same k expertscombined = zeros.index_add(0, self._batch_index, stitched.float())# add eps to all zero values in order to avoid nans when going back to log spacecombined[combined == 0] = np.finfo(float).eps# back to log spacereturn combined.log()def expert_to_gates(self):"""Gate values corresponding to the examples in the per-expert `Tensor`s.Returns:a list of `num_experts` one-dimensional `Tensor`s with type `tf.float32`and shapes `[expert_batch_size_i]`"""# split nonzero gates for each expertreturn torch.split(self._nonzero_gates, self._part_sizes, dim=0)class MLP(nn.Module):def __init__(self, input_size, output_size, hidden_size):super(MLP, self).__init__()self.fc1 = nn.Linear(input_size, hidden_size)self.fc2 = nn.Linear(hidden_size, output_size)self.relu = nn.ReLU()self.soft = nn.Softmax(1)def forward(self, x):out = self.fc1(x)out = self.relu(out)out = self.fc2(out)out = self.soft(out)return outclass MoE(nn.Module):"""Call a Sparsely gated mixture of experts layer with 1-layer Feed-Forward networks as experts.Args:input_size: integer - size of the inputoutput_size: integer - size of the inputnum_experts: an integer - number of expertshidden_size: an integer - hidden size of the expertsnoisy_gating: a booleank: an integer - how many experts to use for each batch element"""def __init__(self, input_size, output_size, num_experts, hidden_size, noisy_gating=True, k=4):super(MoE, self).__init__()self.noisy_gating = noisy_gatingself.num_experts = num_expertsself.output_size = output_sizeself.input_size = input_sizeself.hidden_size = hidden_sizeself.k = k# instantiate expertsself.experts = nn.ModuleList([MLP(self.input_size, self.output_size, self.hidden_size) for i in range(self.num_experts)])self.w_gate = nn.Parameter(torch.zeros(input_size, num_experts), requires_grad=True)self.w_noise = nn.Parameter(torch.zeros(input_size, num_experts), requires_grad=True)self.softplus = nn.Softplus()self.softmax = nn.Softmax(1)self.register_buffer("mean", torch.tensor([0.0]))self.register_buffer("std", torch.tensor([1.0]))assert(self.k <= self.num_experts)def cv_squared(self, x):"""The squared coefficient of variation of a sample.Useful as a loss to encourage a positive distribution to be more uniform.Epsilons added for numerical stability.Returns 0 for an empty Tensor.Args:x: a `Tensor`.Returns:a `Scalar`."""eps = 1e-10# if only num_experts = 1if x.shape[0] == 1:return torch.tensor([0], device=x.device, dtype=x.dtype)return x.float().var() / (x.float().mean()**2 + eps)def _gates_to_load(self, gates):"""Compute the true load per expert, given the gates.The load is the number of examples for which the corresponding gate is >0.Args:gates: a `Tensor` of shape [batch_size, n]Returns:a float32 `Tensor` of shape [n]"""return (gates > 0).sum(0)def _prob_in_top_k(self, clean_values, noisy_values, noise_stddev, noisy_top_values):"""Helper function to NoisyTopKGating.Computes the probability that value is in top k, given different random noise.This gives us a way of backpropagating from a loss that balances the numberof times each expert is in the top k experts per example.In the case of no noise, pass in None for noise_stddev, and the result willnot be differentiable.Args:clean_values: a `Tensor` of shape [batch, n].noisy_values: a `Tensor` of shape [batch, n].  Equal to clean values plusnormally distributed noise with standard deviation noise_stddev.noise_stddev: a `Tensor` of shape [batch, n], or Nonenoisy_top_values: a `Tensor` of shape [batch, m]."values" Output of tf.top_k(noisy_top_values, m).  m >= k+1Returns:a `Tensor` of shape [batch, n]."""batch = clean_values.size(0)m = noisy_top_values.size(1)top_values_flat = noisy_top_values.flatten()threshold_positions_if_in = torch.arange(batch, device=clean_values.device) * m + self.kthreshold_if_in = torch.unsqueeze(torch.gather(top_values_flat, 0, threshold_positions_if_in), 1)is_in = torch.gt(noisy_values, threshold_if_in)threshold_positions_if_out = threshold_positions_if_in - 1threshold_if_out = torch.unsqueeze(torch.gather(top_values_flat, 0, threshold_positions_if_out), 1)# is each value currently in the top k.normal = Normal(self.mean, self.std)prob_if_in = normal.cdf((clean_values - threshold_if_in)/noise_stddev)prob_if_out = normal.cdf((clean_values - threshold_if_out)/noise_stddev)prob = torch.where(is_in, prob_if_in, prob_if_out)return probdef noisy_top_k_gating(self, x, train, noise_epsilon=1e-2):"""Noisy top-k gating.See paper: https://arxiv.org/abs/1701.06538.Args:x: input Tensor with shape [batch_size, input_size]train: a boolean - we only add noise at training time.noise_epsilon: a floatReturns:gates: a Tensor with shape [batch_size, num_experts]load: a Tensor with shape [num_experts]"""clean_logits = x @ self.w_gateif self.noisy_gating and train:raw_noise_stddev = x @ self.w_noisenoise_stddev = ((self.softplus(raw_noise_stddev) + noise_epsilon))noisy_logits = clean_logits + (torch.randn_like(clean_logits) * noise_stddev)logits = noisy_logitselse:logits = clean_logits# calculate topk + 1 that will be needed for the noisy gatestop_logits, top_indices = logits.topk(min(self.k + 1, self.num_experts), dim=1)top_k_logits = top_logits[:, :self.k]top_k_indices = top_indices[:, :self.k]top_k_gates = self.softmax(top_k_logits)zeros = torch.zeros_like(logits, requires_grad=True)gates = zeros.scatter(1, top_k_indices, top_k_gates)if self.noisy_gating and self.k < self.num_experts and train:load = (self._prob_in_top_k(clean_logits, noisy_logits, noise_stddev, top_logits)).sum(0)else:load = self._gates_to_load(gates)return gates, loaddef forward(self, x, loss_coef=1e-2):"""Args:x: tensor shape [batch_size, input_size]train: a boolean scalar.loss_coef: a scalar - multiplier on load-balancing lossesReturns:y: a tensor with shape [batch_size, output_size].extra_training_loss: a scalar.  This should be added into the overalltraining loss of the model.  The backpropagation of this lossencourages all experts to be approximately equally used across a batch."""gates, load = self.noisy_top_k_gating(x, self.training)# calculate importance lossimportance = gates.sum(0)#loss = self.cv_squared(importance) + self.cv_squared(load)loss *= loss_coefdispatcher = SparseDispatcher(self.num_experts, gates)expert_inputs = dispatcher.dispatch(x)gates = dispatcher.expert_to_gates()expert_outputs = [self.experts[i](expert_inputs[i]) for i in range(self.num_experts)]y = dispatcher.combine(expert_outputs)return y, loss

https://github.com/davidmrau/mixture-of-experts

MoSE

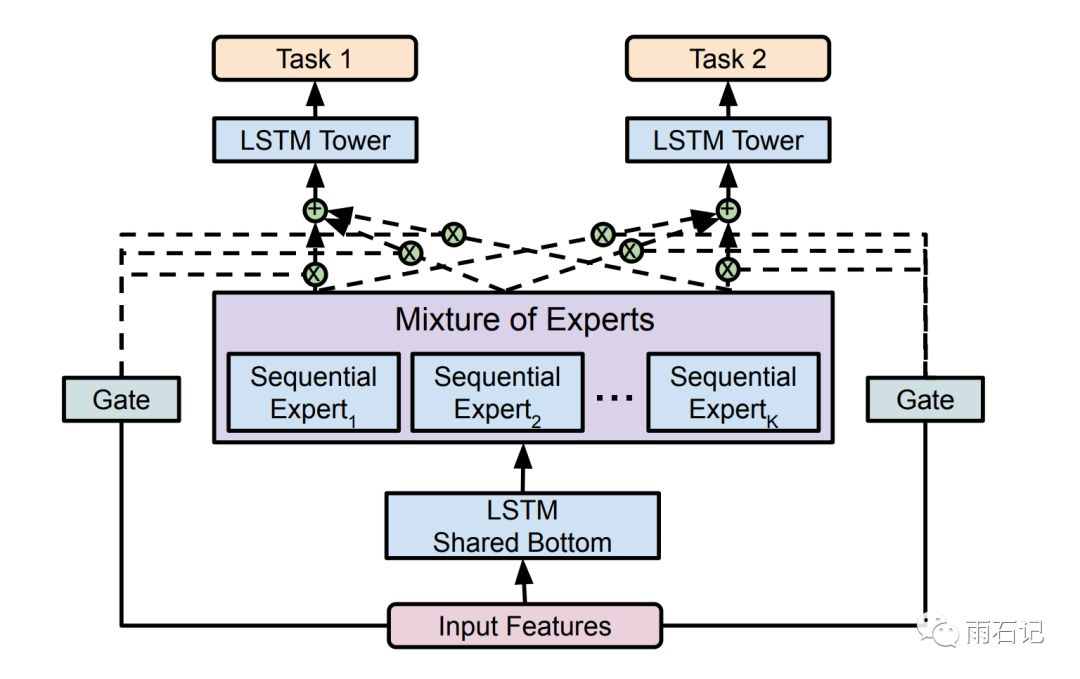
References

GitHub - XueFuzhao/awesome-mixture-of-experts: A collection of AWESOME things about mixture-of-experts

这篇关于混合专家模型 Mixture-of-Experts (MoE)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---