NSDI‘22 - Enabling IoT Self-Localization Using Ambient 5G Signals

计算机网络顶会无线通信类论文解读

NSDI'22 - Enabling IoT Self-Localization Using Ambient 5G Signals

• 计算机网络顶会无线通信类论文解读
• • @[TOC](NSDI'22 - Enabling IoT Self-Localization Using Ambient 5G Signals)
• 1. 背景
• 2. 定位原理
• • 2.1 无线定位的基本原理
  • 2.2 宽带信号处理
  • 2.3 获取CIR
  • 2.4 获取位置
• 三. 其它

1. 背景

传统定位方法缺点：
1）GPS芯片功耗高，不适合低功耗物联网使用
2）基于基站的定位精度低（百米级），或需要与基站进行交互以提升精度但需要对基站进行改造
本文提出了一种无需与基站进行交互的定位技术，其利用5G具有较高的带宽实现了高精度的定位，且对硬件的要求较低。

2. 定位原理

2.1 无线定位的基本原理

5G频谱有着更高的带宽，100MHz的带宽定位精度可以达到3m（$c/B$，c为光速B为带宽），而5G使用的OFDMA子载波间隔$\Delta f=60KHz$，因此定位范围可达5Km（$c/\Delta f$）。在基站位置已知的情况下，通过获取信号从基站到设备的飞行时间（ToF）和到达角（AoA)，从而实现对设备的定位。5G通信中OFDM符号的前导序列可以用来做信道估计，可以获得信道的冲激响应（CIR），但该CIR不能直接计算信号时延，因为该CIR是多径效应叠加的结果，因此可以通过多信号分类（MUSIC）算法来获取LoS分量，从而计算设备距离基站的距离和到达角，进而实现定位。

2.2 宽带信号处理

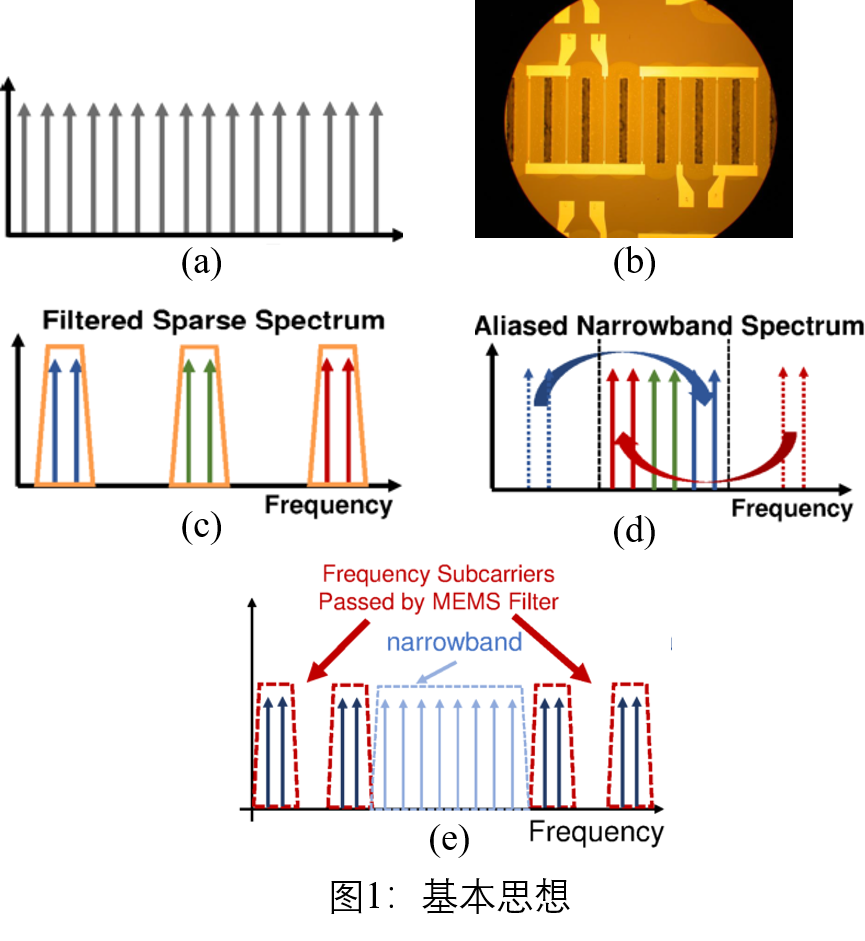
IoT设备的硬件简单，且有着严格的功耗限制，通常不能接收100MHz的高带宽信号。5G中使用的OFDM符号由若干个子载波组成（1024，2048或4096），该符号占据100MHz带宽，如图1(a)所示。本文使用微电子机械系统声学谐振器设计一种脉冲序列滤波器（以下简称该滤波器），该滤波器频域特性如图1(b)所示，其有等间距的脉冲序列组成，脉冲具有一定带宽，在该带宽之内的信号会被保留，脉冲序列之外的信号会被抑制。OFDM符号在过经该滤波器后，仅保留部分子载波，如图1©所示。将滤波后信号经过降采样（本文中使用采样频率6.25MHz，带宽的1/16）后会产生频谱混叠（采样后的频谱原有信号的频谱的周期延拓），混叠结果如图1(d)所示。这样滤波后的子载波就会在一个比较窄的频带内，即在IoT设备的处理范围内，通过估计这些子载波的信道冲激响应（CIR），再从中找出LoS分量后即可测得基站与设备之间的传输延迟进而得出距离完成定位。但需要注意的是，由于该滤波器滤除了部分子载波，使得图1©中子载波密度稀疏，当降采样稀疏为P=16时，即相当于子载波间隔$\Delta f$增大的16倍，使得感知距离减小16倍，即只有312.5m。因此为同时拥有高精度和长距离的定位，除使用前述过程获得高带宽下的CIR外，本文通过直接截取低带宽信号获得原有子载波间隔的子载波集，如图1(f）所示，通过两者的结合来同时保障定位精度和距离。

2.3 获取CIR

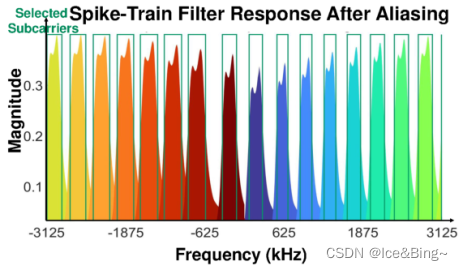
将高带宽但大子载波间隔的子载波集记作$f_M$，将窄带宽窄子载波间隔的子载波集记作$f_{NB}$,本文即同时使用两种子载波$f_{tot}=f_M\cup f_{NB}$进行定位，记$f_{tot}$中的子载波总数为$T$。首先根据OFDM符号的前导序列计算$f_{tot}$的CIR$h_{tot}^{\prime }$，其是一个$T\times 1$维的矢量，但该CIR是多径效应叠加的结果，因此可以使用MUSIC算法从中分离出LoS分量。但由于本文使用的冲激序列滤波器的非理想特性（即脉冲序列的边缘并非陡峭的），会使得降采样后子载波在边界上产生一定的混叠，这会影响CIR估计的精度，因此在估计CIR时仅使用未混叠在一起的部分，如图2所示。可以看到这种对频谱的截取是不均匀的，因此MUSIC算法不再适用，本文将该问题转化为优化问题，从而同样能够得出多径传播下不同路径的时延。

图2. 冲激序列滤波器频响应的混叠模式

假定多径传播中共有L条路径，则连续信道的CIR为
$$CI{R}_{cont}=\sum _{l=1}^L{a}_l\delta \left(\tau -{\tau }_l\right)$$
其中$a_l$和${\tau }_l$分别为第$l$条路径的幅度增益和时延。由于带宽为$B$时定时精度为$1/B$秒，因此实际得到的时延${\tau }_g$是离散化的，取值为${\tau }_g\in \left\{\frac{0}{B},\dots ,\frac{(N-1)}{B}\right\}$,因此离散化的CIR为：
$$CI{R}^{\text{net }}\left({\tau }_g\right)=\sum _{l=1}^L{a}_l{\psi }_N\left({\tau }_g-{\tau }_l\right)$$
其中${\psi }_N$为离散$sinc$函数，表达式为：
$${\psi }_N(\tau )=\frac{\sin (\pi \tau )}{\sin \left(\frac{\pi \tau }{N}\right)}\exp (-\pi j\left(\frac{N-1}{N}\right)$$
$CI{R}^{\text{net }}$为$N\times 1$的矢量，其中N表示一个OFDM符号中子载波总数，求$\vec{a}$和$\vec{\tau }$可转化为以下L2优化问题：
{ τ l ∗ , a l ∗ } l = 1 L = arg ⁡ min ⁡ τ 1 , … , τ L , a 1 , … , a L ∥ h t o t ′ − V F N Ψ a ⃗ ∥ 2 \left\{\tau_{l}^{*}, a_{l}^{*}\right\}_{l=1}^{L}=\underset{\tau_{1}, \ldots, \tau_{L}, a_{1}, \ldots, a_{L}}{\arg \min }\left\|h_{t o t}^{\prime}-\mathbf{V} \mathbf{F}_{N} \Psi \vec{a}\right\|^{2} {τl∗​,al∗​}l=1L​=τ1​,…,τL​,a1​,…,aL​argmin​∥htot′​−VFN​Ψa ∥2
其中$\Psi$为$N\times L$矩阵，${\Psi }_{i,j}={\psi }_N\left({\tau }_i-{\tau }_j\right)$；${\mathbf{F}}_N$为$N\times N$的DFT矩阵；$\mathbf{V}$为$T\times N$矩阵用于从N个子载波中获取$f_{tot}$。$\Psi$已知时，带入$\vec{a}={\left(\mathbf{V}{\mathbf{F}}_N\Psi \right)}^{†}{h}_{tot}^{\prime }$，$†$表示求违逆，则上述优化转化为L1优化：
{ τ l ∗ } l = 1 L = arg ⁡ min ⁡ τ 1 , … , τ L ∥ h tot  ′ − V F N Ψ ( V F N Ψ ) † h t o t ′ ∥ 2 s.t.  τ l ≥ 0 ∀ l ∈ { 1 , 2 , … , L } \begin{aligned} &\left\{\tau_{l}^{*}\right\}_{l=1}^{L}=\underset{\tau_{1}, \ldots, \tau_{L}}{\arg \min }\left\|h_{\text {tot }}^{\prime}-\mathbf{V} \mathbf{F}_{N} \Psi\left(\mathbf{V} \mathbf{F}_{N} \Psi\right)^{\dagger} h_{t o t}^{\prime}\right\|^{2} \\ &\text { s.t. } \tau_{l} \geq 0 \quad \forall l \in\{1,2, \ldots, L\} \end{aligned} ​{τl∗​}l=1L​=τ1​,…,τL​argmin​∥∥∥​htot ′​−VFN​Ψ(VFN​Ψ)†htot′​∥∥∥​2 s.t. τl​≥0∀l∈{1,2,…,L}​
可以适用内点法对$\vec{\tau }$进行估计，从而得到ToF。

2.4 获取位置

对设备定位的基本前提是基站位置是已知的，5G基站位置信息很容易通信协议得到。由于5G基站不与IoT设备严格同步，由于硬件电路中存在采样时间偏差（STO），因此2.3节得到的ToF是包含采样偏差的，因此可以在IoT设备上使用两根天线，用差分ToF代替绝对ToF，如图3所示。

图3. 差分ToF模型

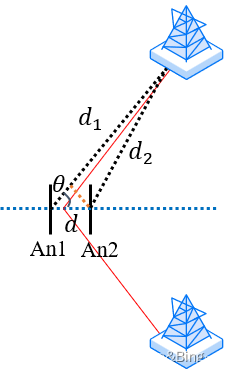
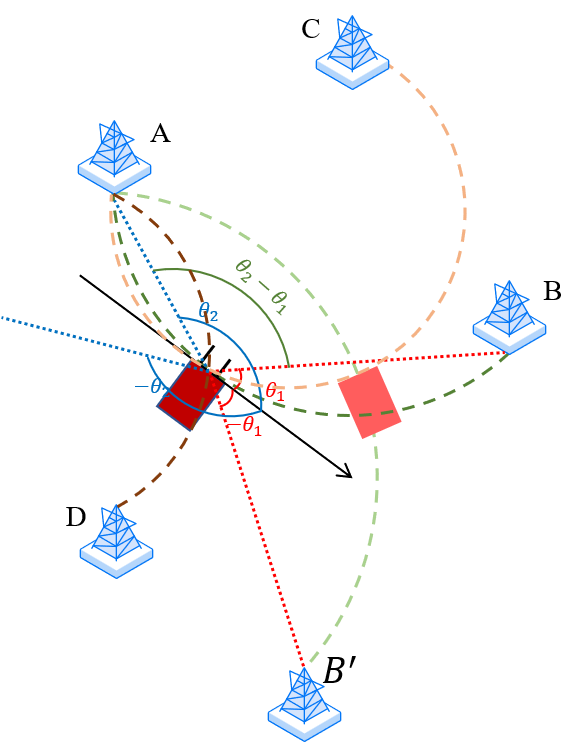
其中$d_1$与$d_2$是2.3节中测得的绝对ToF对应的距离，由于STO的影响，他们都不是基站距离设备的精确距离，但由于两根天线共用一套RF链，有着相同的STO，因此它们的差是恒定的，因此有$dcos(\theta )=d_1-d_2$,其中$d$为两天线间距，据此可以求出基站与设备天线水平面的夹角$\theta$。但由于该角是相对两天线组成的平面而言的，不是绝对位置，因此借鉴拆分ToF的思想，两基站相对到达角分别为${\theta }_1$和${\theta }_2$,则它们的差值$|{\theta }_2-{\theta }_1|$为一定值。考虑在圆之中同弧所对的圆周角相同，因此两基站与设备在同一个圆上，如图4所示。

图4. 双基站确定设备所在位置范围

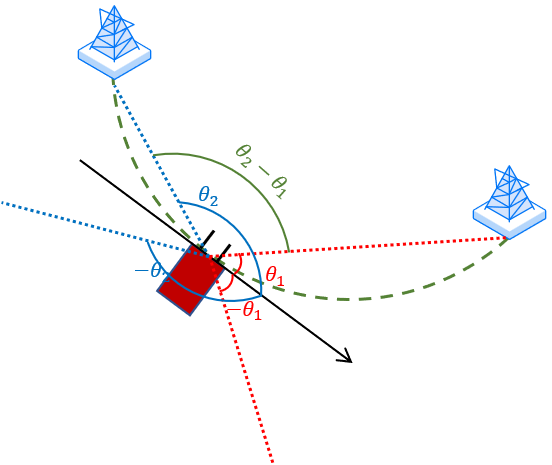
图3中计算得到相对到达角$\theta$无法判定基站位于设备的上（北）面还是下（南）面，这就造成了设备位置模糊性，则图中圆弧对应的夹角不一定是$|{\theta }_2-{\theta }_1|$，还有可能是$|{\theta }_2+{\theta }_1|$，因此使用三台基站进行定位时就会出现位置模糊性。如图5所示，基站B可能出现在两个位置，此时使用$ABC$与$A{B}^{\prime }C$进行定位会得到不同的结果。此时使用四个基站进行定位，以其中一个基站作为公共点可得三个圆弧，三个圆弧的交点即为设备位置，这样便可消除模糊性。

图5. 设备定位

三. 其它

1. 引理5.1说明了在何种情况下降采样得到的重叠谱会保留原有状态信息：即降采样系数P可以被子载波数N整除；
2. 引理5.2说明了满足条件的冲激序列滤波器的参数如何选择

https://www.usenix.org/conference/nsdi22/presentation/jog