暑假训练---三棱锥内切球公式及海伦公式

本文主要是介绍暑假训练---三棱锥内切球公式及海伦公式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目 2326: 七月树的水题

题目描述
七月树看到了一道题。“哇！水题啊！”七月树愉快地叫着，看样子她 AK
稳了。

七月树看到的题如下：
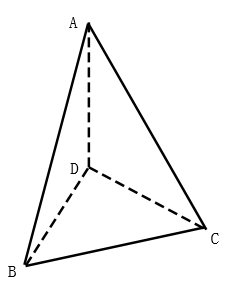
有一个如图的三棱锥，其中 AD,BD,CD 两两互相垂直。
已知 AD,BD,CD 的长度，求该三棱锥内切球的最大体积。

在这里插入图片描述

输入
三个整数 a,b,c，表示 AD,BD,CD 的长度。
输出
三棱锥内切球的体积，保留 2 位小数。
样例输入
1 1 1
样例输出
0.04

设内切球bai球 O 则 O 三棱锥四面du任距离 R ，

由 O 顶点别三棱锥四面底面四三棱锥则高zhi均 R 底面面dao积总 S 体积 V 。

V = V1 + V2 + V3 + V4，

V = RS1/3 + RS2/3 + RS3/3 + RS4/3，

V = R*S/3 R=3V/S

扩展资料：

如果一个球与简单多面体的各面或其延展部分都相切，且此球在多面体的内部，则称这个球为此多

面体的内切球(inscribed sphere of a polyhedron)。多面体称为这个球的外切多面体，正多面体的

内切球均存在，正多面体内任意点到各面距离之和为常数。
在这里插入图片描述
与圆台的上、下底面以及每条母线都相切的球，称为圆台的内切球(inscribed sphere in a frustum of a circular cone)，此圆台称为球的外切圆台，当且仅当母线长与上、下两底面圆半径之和相等时，圆台才有内切球。

海伦公式：
已知三角形三边a,b,c，则：

（海伦公式）（p=(a+b+c)/2）

S=sqrt[p(p-a)(p-b)(p-c)]

=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

在这里插入图片描述

//三角形内切球得体积
//公式，内切球半径 = （三棱锥体积）/（三棱锥表面积）
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define pi 3.1415926535
using namespace std;int main()
{double a,b,c;cin>>a>>b>>c;//除底边外其他三个面积 double s1 = a*b/2;double s2 = a*c/2;double s3 = b*c/2;double x1,x2,x3;//斜边 x1 = sqrt(a*a+b*b);x2 = sqrt(a*a+c*c);x3 = sqrt(b*b+c*c);double p,s4;p = (x1+x2+x3)/2; //海伦半长公式s4 = sqrt(p*(p-x1)*(p-x2)*(p-x3)); double r,v;r = s3*a/(s1+s2+s3+s4); //三棱锥内切球公式 r = 3*V/(S) ；；S为总面积 if(a==0||b==0||c==0){printf("0.00");return 0;}v = pi*r*r*r*4/3; //球得体积公式printf("%.2f",v);return 0;}