Ceres-solver学习笔记-pose_graph_2d.cc

[本节官方教程链接🔗](http://ceres-solver.org/nnls_tutorial.html#f9)
pose_graph_2d.cc针对SLAM问题中的位姿图优化问题，
如下，三角点xi表示物体的状态，边zij表示观测，即xi和xj之间的约束，
实线边表示两个状态之间是序列性的（sequential ），虚线则表示非序列性即闭环的两帧之间的约束。

其中，x由一个表示平移的二维向量p和一维标量φ （弧度制），则观测Zab由Pab及φab表示观测到的a、b两个状态的约束。则应该在ceres实现的cost function中的误差为：

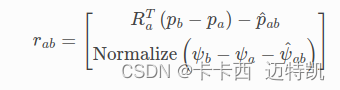
其中要将角度残差归一化(角度范围为[-π，π))，其中Ra^T为：

最后，考虑到测量的不确定度，需要对残差用信息矩阵进行加权，ceres并没有自动加权，所以要手动给残差左乘一个残差的开方的转置。
程序运行用到了g2o格式的数据文件，g2o数据文件

（详细运行看自己下载的ceres文件夹里examples里相对应的 readme）

程序运行：/path/to/bin/pose_graph_2d --input /path/to/dataset/dataset.g2o
观看输出结果：/path/to/repo/examples/slam/pose_graph_2d/plot_results.py --optimized_poses ./poses_optimized.txt --initial_poses ./poses_original.txt

• ceres解决优化问题无非两步，建立优化问题然后solve，solve没什么好说的，基本就是选择ceres中定义好的参数往ceres库中的函数传参，建立一个简单的非线性最小二乘优化问题需要：
  1.首先确定好损失函数loss function和定义好基于类对象或结构体对象“函数子”即cost functor的cost function，在cost functor中重载operator()定义残差函数，至于残差对优化变量的导数可用ceres中的自动求导，也可以自行定义。
  2.之后将cost function,lossfunction,各个之间存在约束关系的优化变量加入AddResidualBlock函数中

详细步骤即细节看如下代码注释

// Constructs the nonlinear least squares optimization problem from the pose
// graph constraints.
void BuildOptimizationProblem(const std::vector<Constraint2d>& constraints,std::map<int, Pose2d>* poses,ceres::Problem* problem) {CHECK(poses != NULL);CHECK(problem != NULL);if (constraints.empty()) {LOG(INFO) << "No constraints, no problem to optimize.";return;}//损失函数即鲁棒核函数，鲁棒核函数的主要作用是降低数据中明显错误的数据对优化的影响ceres::LossFunction* loss_function = NULL;//这里LocalParameterization是针对某些优化优化参数过参数化的问题，//例如，对于一个球体上点坐标的优化问题来说，一个点的坐标p=[x,y,z]，//但是由球的流形可知其只有两个自由度，因此我们可以仅仅优化两个参数，之后再更新优化后的点ceres::LocalParameterization* angle_local_parameterization =AngleLocalParameterization::Create();for (std::vector<Constraint2d>::const_iterator constraints_iter =constraints.begin();constraints_iter != constraints.end(); ++constraints_iter) {const Constraint2d& constraint = *constraints_iter;std::map<int, Pose2d>::iterator pose_begin_iter =poses->find(constraint.id_begin);CHECK(pose_begin_iter != poses->end())<< "Pose with ID: " << constraint.id_begin << " not found.";std::map<int, Pose2d>::iterator pose_end_iter =poses->find(constraint.id_end);CHECK(pose_end_iter != poses->end())<< "Pose with ID: " << constraint.id_end << " not found.";const Eigen::Matrix3d sqrt_information =constraint.information.llt().matrixL();//求开根号的信息矩阵// Ceres will take ownership of the pointer.//定义残差函数ceres::CostFunction* cost_function = PoseGraph2dErrorTerm::Create(constraint.x, constraint.y, constraint.yaw_radians, sqrt_information);//构建残差块problem->AddResidualBlock(cost_function, loss_function, &pose_begin_iter->second.x,&pose_begin_iter->second.y, &pose_begin_iter->second.yaw_radians,&pose_end_iter->second.x, &pose_end_iter->second.y,&pose_end_iter->second.yaw_radians);//设置LocalParameterization的优化变量problem->SetParameterization(&pose_begin_iter->second.yaw_radians,angle_local_parameterization);problem->SetParameterization(&pose_end_iter->second.yaw_radians,angle_local_parameterization);}//固定第一个优化参数，即第一个参数不优化//因为我们获得的观测都是状态间的相对量，因此最后优化出的轨迹还有一个轨迹位置的不确定性，//即最后得到的轨迹形状是一样的但是其起始位置很可能不同，//举个例子，你在两个不同的房间可以走出相同形状的轨迹，但是轨迹的绝对位置是不一样的，//当固定第一个优化变量后，轨迹位置的不确定性也就消失了std::map<int, Pose2d>::iterator pose_start_iter =poses->begin();CHECK(pose_start_iter != poses->end()) << "There are no poses.";problem->SetParameterBlockConstant(&pose_start_iter->second.x);problem->SetParameterBlockConstant(&pose_start_iter->second.y);problem->SetParameterBlockConstant(&pose_start_iter->second.yaw_radians);
}// Returns true if the solve was successful.
bool SolveOptimizationProblem(ceres::Problem* problem) {CHECK(problem != NULL);ceres::Solver::Options options;options.max_num_iterations = 100;//迭代次数//柯西分解求解具有稀疏性的大规模非线性最小二乘问题options.linear_solver_type = ceres::SPARSE_NORMAL_CHOLESKY;ceres::Solver::Summary summary;ceres::Solve(options, problem, &summary);std::cout << summary.FullReport() << '\n';return summary.IsSolutionUsable();
}