本文主要是介绍【目标检测】30、Rectified IoU: Single-Shot Two-Pronged Detector with Rectified IoU Loss,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

文章目录
- 一、背景
- 二、方法
- 三、效果
论文:Single-Shot Two-Pronged Detector with Rectified IoU Loss
代码:暂无
出处:ACM MM 2020
一、背景
在检测任务重,IoU 经常被用来选择预选框,但这种直接的做法也忽略了样本分布的不均衡的特点,这会影响定位 loss 的梯度,从而影响最终的效果。
作者思考,能不能在训练的过程中不断 rectify 所有样本的梯度,来提升效果。于是就提出了 Rectified IoU (RIoU) loss。
Rectified IoU (RIoU) loss 的目的:增大 high IoU 样本的梯度,抑制 low IoU 样本的梯度
Rectified IoU (RIoU) loss 的特点:在使用 RIoU 训练时,大量简单样本(IoU 大)的梯度会被增大,让网络更关注这些样本,而少量的难样本(IoU 小)的梯度会被抑制。这样会使得每种类型的样本的贡献更均衡,训练过程更高效和稳定。
为什么抑制难样本的梯度后,每类样本的贡献会更均衡呢?
因为 IoU 低的样本占大多数,所以对应的 loss 更大,所以作者通过提高简单样本对 loss 的贡献,来让难易样本的贡献更均衡。
二、方法
L I o U L_{IoU} LIoU 的形式如下:
L I o U = 1 − I o U L_{IoU}=1-IoU LIoU=1−IoU
L I o U L_{IoU} LIoU 的偏导如下:
∣ g r a d i e n t s ( I o U ) ∣ = ∣ ∂ L I o U ∂ I o U ∣ = 1 |gradients(IoU)|=|\frac{\partial L_{IoU}}{\partial_{IoU}}|=1 ∣gradients(IoU)∣=∣∂IoU∂LIoU∣=1
由此可看出, ∣ g r a d i e n t s ( I o U ) ∣ |gradients(IoU)| ∣gradients(IoU)∣ 是一个常数,对难易样本无差别对待,但不同 IoU 样本的分布是很不均衡的。low IoU 样本的数量大于 high IoU 样本的数量,也就是说,在训练过程中,low IoU 样本掌握着梯度,让网络更偏向于难样本的回归。
Rectified IoU (RIoU) loss 的目的:增大 high IoU 样本的梯度,抑制 low IoU 样本的梯度
如何修正呢:
如果梯度总是随着 IoU 的增大而增大,则会面临一个问题,即当某个框回归的非常好时( I o U → 1 IoU \to 1 IoU→1),其梯度会最大,这是不合适的。
所以作者提出了如下的方式,a, b, c, k 可以控制梯度曲线的形状。上升后,在 I o U = β IoU =\beta IoU=β 处快速下降,本文 β = 0.95 \beta=0.95 β=0.95。
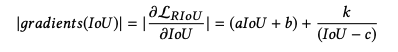
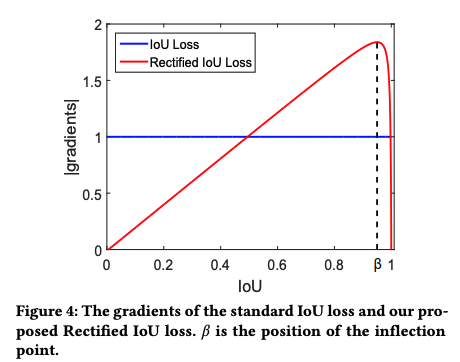
当 β = 0.95 \beta=0.95 β=0.95 时的 Loss 曲线对应如下, I o U < β IoU<\beta IoU<β 时是凸型, I o U > β IoU>\beta IoU>β 时是凹型:
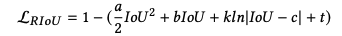
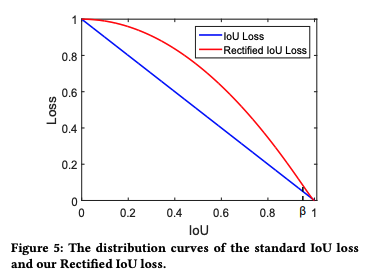
三、效果
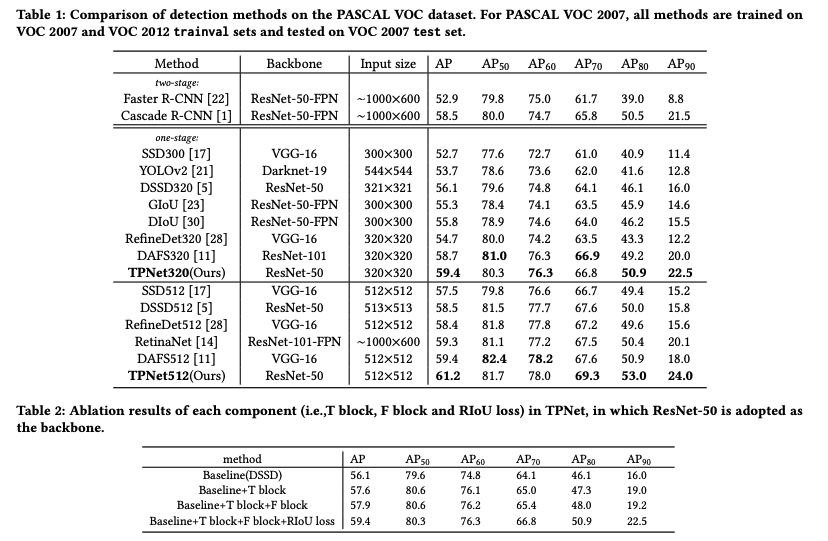
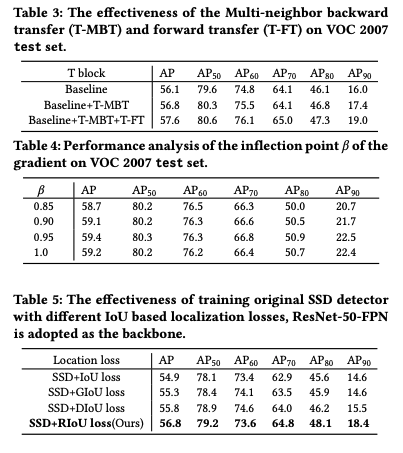
这篇关于【目标检测】30、Rectified IoU: Single-Shot Two-Pronged Detector with Rectified IoU Loss的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







