Mel频谱和MFCC深入浅出

前言

在音频领域，mel频谱和mfcc是非常重要的特征数据，在深度学习领域通常用此特征数据作为网络的输入训练模型，来解决音频领域的各种分类、分离等业务，如端点侦测、节奏识别、和弦识别、音高追踪、乐器分类、音源分离、回声消除等相关业务。

当然，针对深度学习音频领域的业务，不是用下这两个特征、选几个网络、打个标签，放数据训练就完事了， 仅仅基于mel频谱和mfcc这两个特征，解决好上述业务某些情况下还是远远不够的，熟悉这些特征的内在逻辑性、衍生细节和延展，才能更好的结合深度学习解决业务问题。

下面讲解mel频谱和mfcc特征的算法流程和一些细节、延展，这些细节从局部角度来看，都会影响到最终特征呈现的细节差异，这些差异放大到模型训练结果的准确性、鲁棒性上怎么样是非常值得研究的，某些情况下可能会有质的变化，质的变化无论正向还是负向都是值得关注的，最怕的是没变化；同时，一些问题的延展从广义角度来看，带来不同的特征组合、网络结构设计思考等也是解决业务问题非常重要的思想源泉。

算法流程

设 sr 为采样率，fftLength 为帧长度，slideLength 为滑动长度

下面是一张mel频谱和mfcc的大概算法流程图。

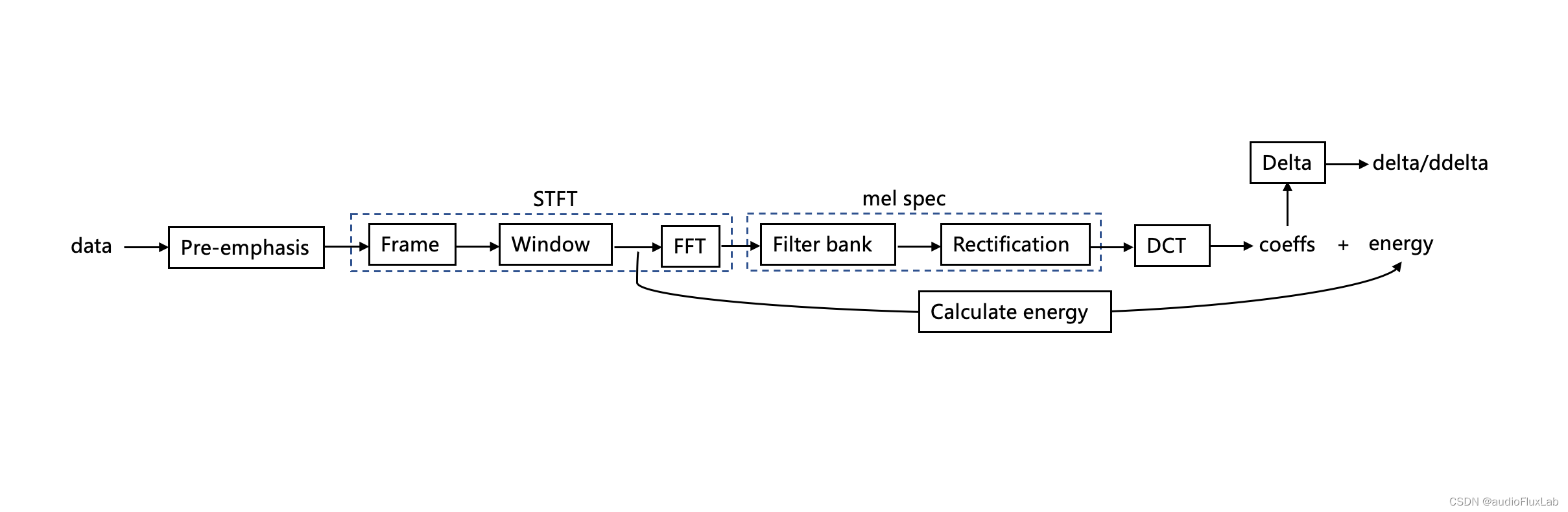
1. 预加重（Pre-emphasis）

如流程图所示的第1步，属于信号的预处理，补偿高频分量损失，提升高频分量，一般情况下可以忽略此步骤，属于信号的简单增强，对特征有一定的提升效果。公式如下

$$x[n]=x[n]-\alpha x[n-1]$$

$\alpha$一般取0.97
公式属于差分一阶即高通滤波器。

2. 分帧（Frame）

现实中大多数信号都是非平稳的，但大多数短时间内可以近似看做是平稳的，可以用短时傅里叶变换表现非平稳信号频域特征。 一般语音中采用10ms~30ms左右，乐音中可以更长一些64ms~256ms。

分帧涉及到前后重叠（overlap），一般情况下以滑动帧长的1/4或1/2（前后重叠3/4或1/2）进行，即$slideLength=\frac{fftLength}{4}或\frac{fftLength}{2}$。

3. 加窗（Window）

加窗目的是减少频谱泄露，降低泄漏频率干扰，提升频谱效果，默认不处理即加矩形窗（Rect），干扰泄漏较严重，一般情况下加Hann窗，针对大多数信号都有不错的效果。公式如下
$$w(n)=0.5\left(1-\cos \left(2\pi \frac{n}{N}\right)\right),0\le n\le N$$

Hann为余弦窗，N表示阶数。

4. 短时傅里叶变换（STFT）

分帧加窗傅里叶变换即短时傅里叶变换。公示如下
$$X(\tau ,f)={\int }_{-\infty }^{\infty }x(t)w(t-\tau )e^{-j2\pi ft}dt$$
$$X(m,k)=\sum _{n=0}^{N-1}x[n]W[n-m]e^{\frac{-j2\pi kn}{N}}$$

设数据长度为 dataLength，
$t=\{\begin{array}{ll}\frac{(dataLength-fftLength)}{slideLength}+1,& 无填充\\ \frac{dataLength}{slideLength}+1,& 填充fftLength\end{array}$

STFT属于标准的数学变换，为复数域，尺寸为 $t\ast fftLength$，为表示区分，一般的如$|X(m,k)|$取模，尺寸为$t\ast (fftLength/2+1)$ 表示为STFT频谱，有以下类型频谱。

$|X(m,k)|$，STFT幅值频谱
$|$