本文主要是介绍GAMES101-现代计算机图形学入门-闫令琪 - lecture4 观测变换(viewing transformation) - 课后笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
观测变换(Viewing transformation)
- 视图 / 相机变换(View / Camera transformation)
- 投影变换(Projection transformation)
- 正交投影(Orthographic projection)
- 透视投影(Perspective projection)
视图/相机变换(View / Camera transformation)
什么是视图变换?
思考下如何去拍摄一张照片:
- 找到一个好地方,并且调整人的姿势,(只对模型进行了变换(model transform))
- 调整一个合适的角度,放置摄像机(view transformation)
- 茄子!(将3d转化为2d,投影变换(projection transformation))
图形就是按照上面的步骤进行变换,最终获得屏幕上的2D图像,这之中进行了三次变换,分别是模型变换(model transformation)、视图变换(view transformation)、投影变换(projection transformation),简称MVP ,这节中主要说视图变换。
视图变换操作的主要对象是相机,然后其他的物体跟着变换。
如何实现一个视图变换?
视图变换是对摄像机进行操作,所以需要先定义一个Camera,定义一个Camera需要:
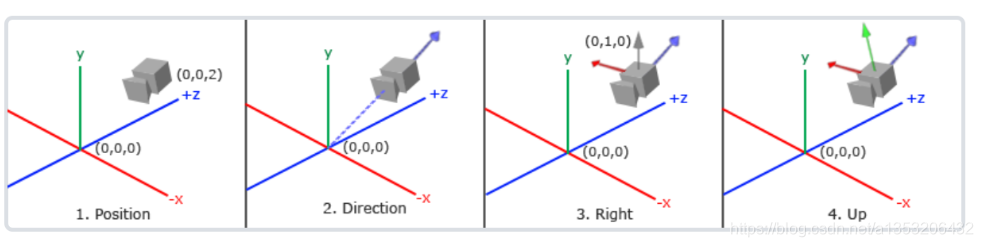
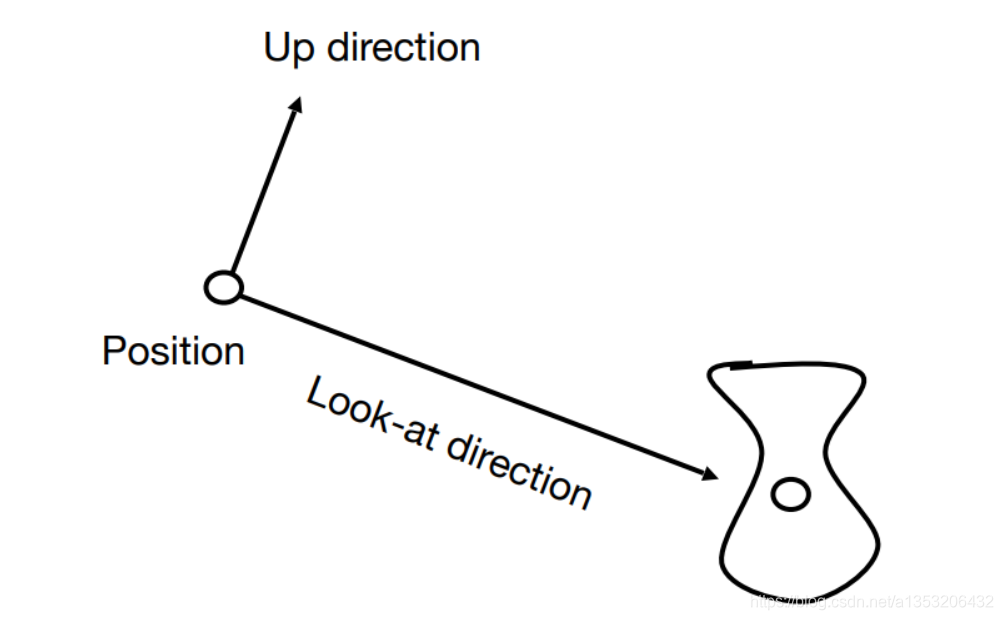
- Camera的位置 e (Position)
- Camera的观察方向 g (Look-at / gaze direction),
- Camera的上方向 t(Up direction),上方向用于固定摄像机的角度,如t指向正上方,那么摄像机就是正的,若t指向斜上方,那么Camera拍出来的图片就是斜的
- Camera的右方向 g × t
如果把Camera看作空间中的一个物体,若将Camera和其他的物体同时进行移动(进行同一种的位移变换),那么其他的物体和Camera就会是一种相对静止,则Camera中显示的画面就永远不会发生改变,所以要希望能够通过Camera观察不同的物体以及转换视角,必须要让Camera和空间中的其他物体实现相对运动。
只移动物体或者只移动Camera,最后可能都会得到同一个结果。那么既然这样的话,不如永远把Camera固定到原点的位置,并且Up方向指向y轴方向,Look-at方向指向-z轴的方向。这样就认为其他所有的物体在移动,而相机并不移动,为什么这么做?老师说这是大家约定俗成的一个东西。其实因为相机放在(0,0,0)的位置有很多的好处,相机沿着-z看也会有很多的好处。所以这个约定的相机位置就是一个标准位置。
那么怎么操作才能把相机放到原点的位置,并且Up指向y方向,Look-at指向z方向?
相机到达这个标准位置,需要经过平移和变换,那么就用一个变换矩阵来完成相机到原点的过程。该矩阵为:
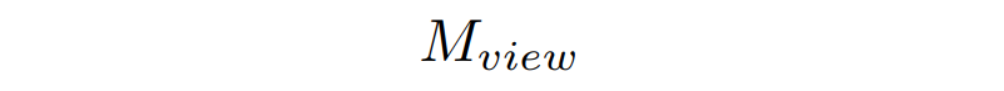
那么这个M(view)矩阵在数学上怎么实现?将下面多个变化叠加,最终可以得到M(view)矩阵.
- 先将Camera的position变换到原点(origin)
- 将g旋转到-z轴方向
- 将t旋转到y轴方向
- 将g×t旋转到x轴方向
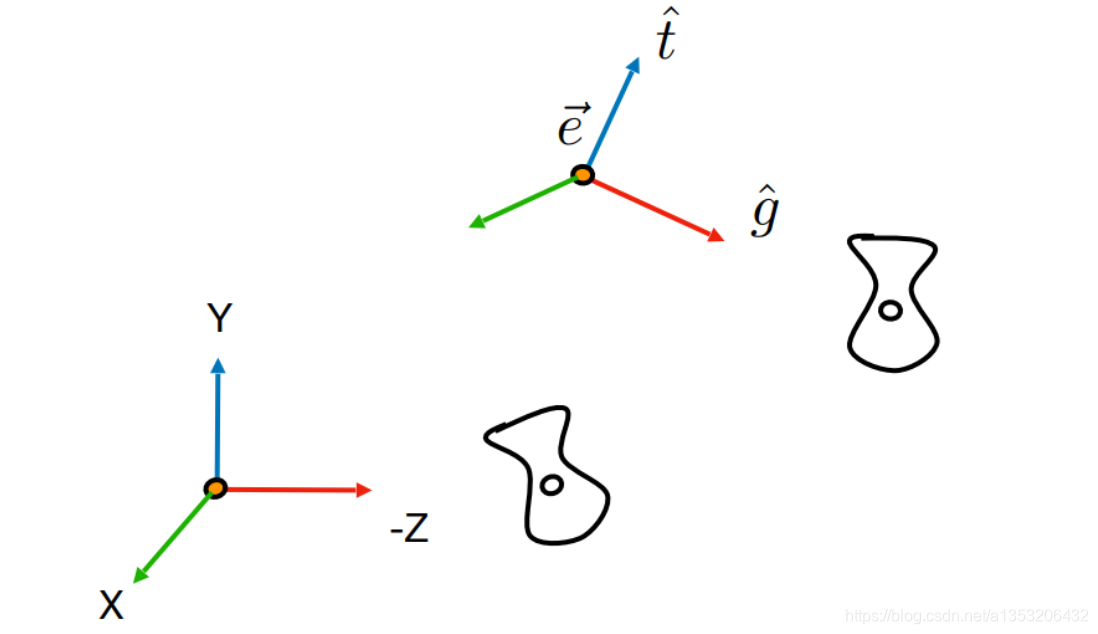
M(view)矩阵的具体实现:
将M(view)矩阵分解为R(view)和T(view)两种变换矩阵,其中T(view)为位移矩阵,将Camera的position移动到原点,R(view)为旋转矩阵,将Camera的几个方向轴旋转到坐标系的位置。
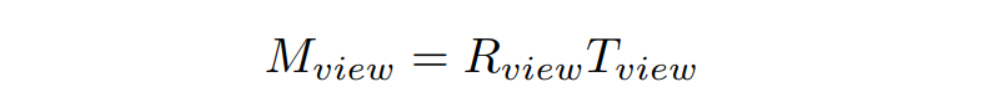
T(view)矩阵,将Camera的position移动到原点,即将(xe,ye,ze)移动到(0,0,0),则x,y,z上的位移量分别为-xe,-ye,-ze。
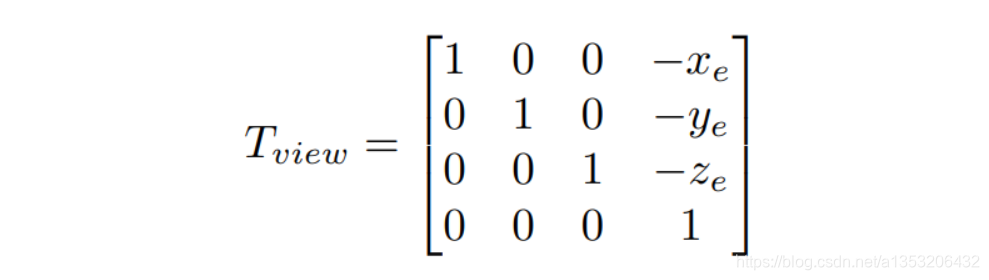
R(view)矩阵要做的事就是将g旋转到-z轴,t旋转到Y轴,(g × t)旋转到x轴。如果这样直接旋转太麻烦,-z轴的方向向量为(0,0,-1),y轴的方向向量为(0,1,0),x轴的方向向量为(1,0,0),明显可以看出,从-z旋转到g,从y旋转到t,从x轴旋转到(g×t)更为简单,这个旋转矩阵为:
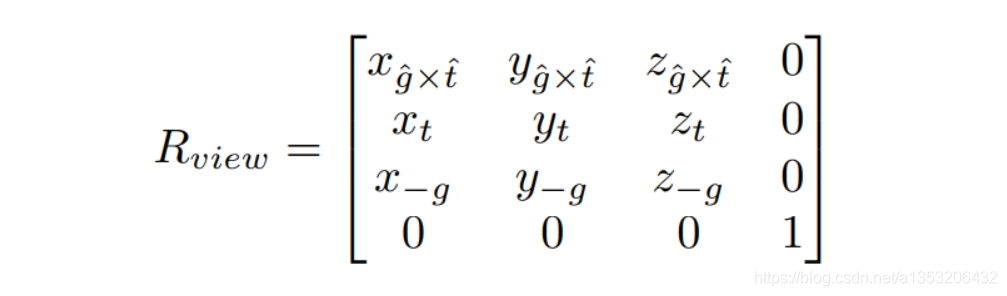
再求这个矩阵的逆矩阵,即逆变换,就可以得到Camera的三个方向旋转到坐标系的三个轴的变换矩阵。因为旋转矩阵都是正交矩阵,所以其逆矩阵 = 转置矩阵。
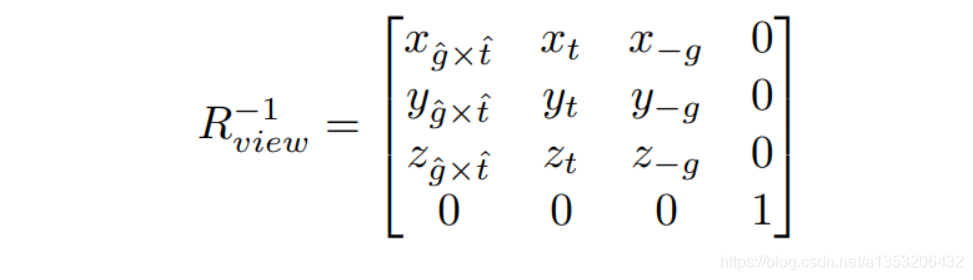
得到了以上的两个变换矩阵后,就可以将Camera的位置设置在原点,并以-z轴为look-at方向,以y轴为up方向。就可以认为Camera是始终不动,变换的一直是Camera以外的其他的物体
相机/视图变换总结
投影变换(Projection transformation)
在图形学中,投影就是将3D的图形投影到2D的平面上,即将三维物体转换成能在能在屏幕上显示的二维图像。
投影变换分为正交投影和透视投影
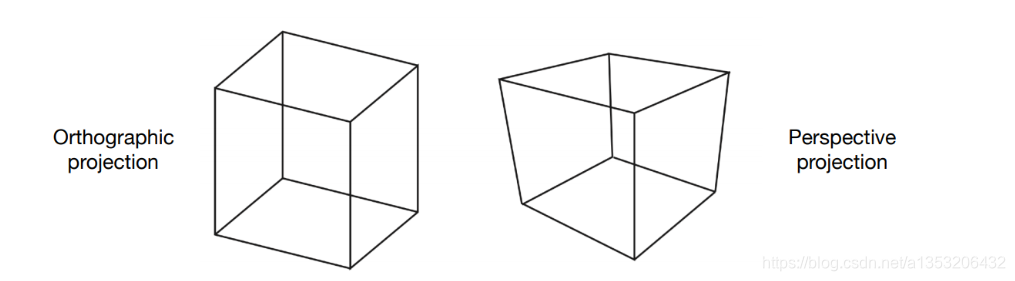
左图为正交投影,右图为透视投影。透视投影进大远小,更符合人眼的观察效果;正交投影不具有进大远小的性质,正交投影是假设Camera位于无限远的位置,投影出来的物体不论近处还是远处,大小都是一样大,更适用于工程制图。具体情况如下所示:
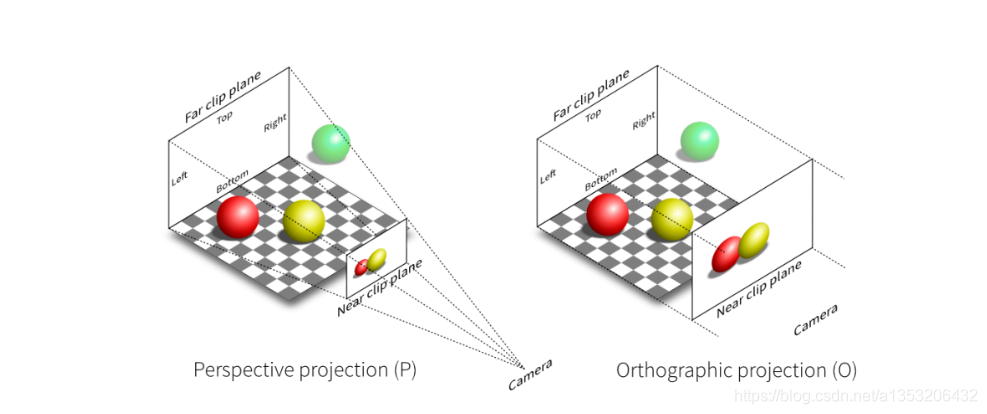
左图为透视投影,透视投影的近平面和远平面的大小不同,会将平截头体内部的物体投影到近平面上(绿球在外面,所以没有投影进来),并且离近平面(near clip plane)近的物体较大,远的物体的投影较小。右图为正交投影,而正交投影则是将正方体内物体投影到近平面上,假设Camera在无限远处,那么所有的投影都是以平行光的方式进行投影到近平面上,所以不具有近大远小的效果。(只有在近平面(near clip plane)和远平面(far clip plane)内的物体才能被投影到近平面上)。
正交(射)投影(Orthographic Projection)
正交投影是把Camera固定在原点上,look-at方向为-z轴,up方向为y轴,如果要对物体进行正交投影,只需要将三维坐标中的z坐标直接丢弃,就能够得到投影的结果,如图所示,投影平面为z = 0,直接丢弃z坐标或者直接令z坐标为0,就可以得到投影的效果。
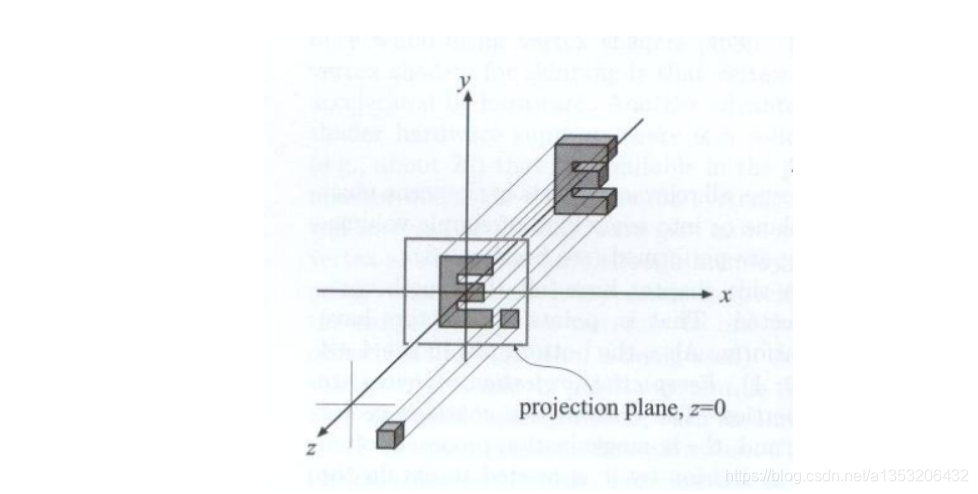
正交投影最后会被缩放到一个[-1,1]的区间范围内,即所有的点的坐标的分量都是在[-1,1]之间的,如果在范围之外则会缩放到[-1,1]之间,这是一个约定俗成的规定。
但是正交投影无法区分前后关系,如上图所示,得到的投影面如下:
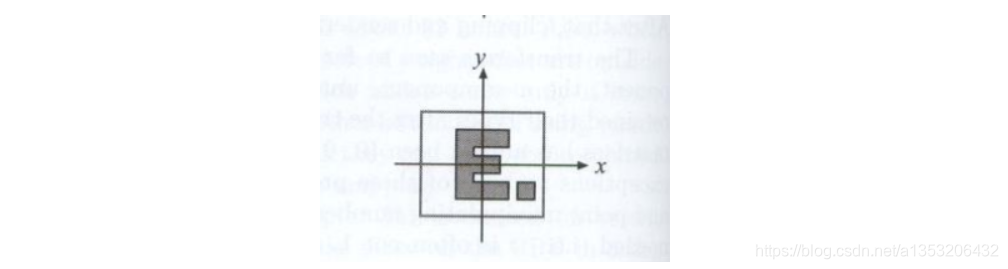
你并不能判断E在前面还是方块在前面。
那么,如果我有一个立方体,我应该如把它转换到[-1,1]之间?
在坐标系统,使用六个数即可定义个立方体(如x=1代表一个面,x=-1代表一个面,六个数定义6个面,包围起来的立体就是立方体),用 l(left) , r(righit) , b(bottom) , t(top) , f(far) , n(near)六个数定义一个立方体.
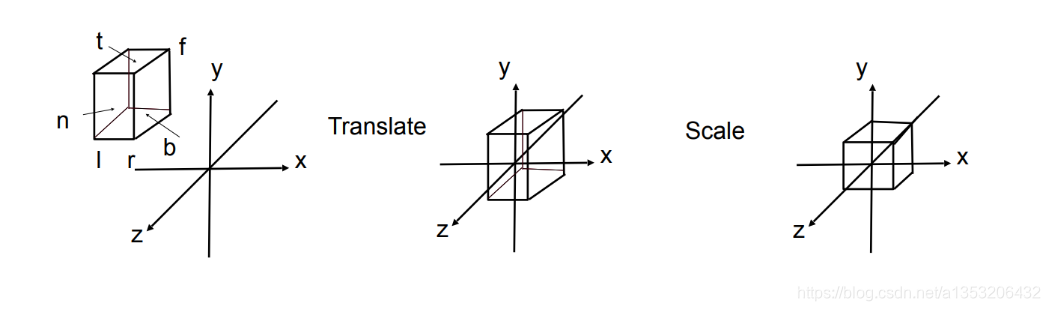
最右边的立方体经过位移,缩放,最终投影的立方体在[-1,1]之间。而转换的矩阵是:
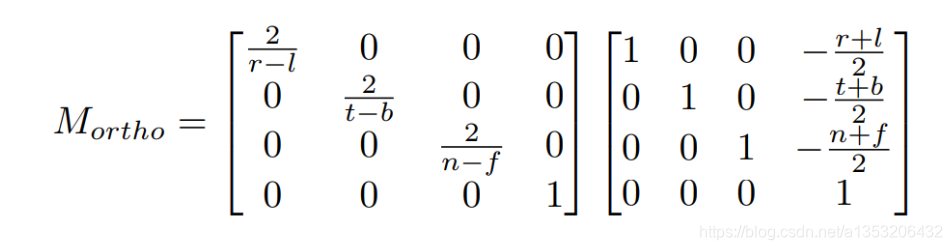
右边的矩阵先与点(表示点的坐标的向量)结合,将物体位移到原点,然后左边的矩阵对其进行缩放。
透视投影(Perspective Projection)
- 在图形学、艺术以及视觉上最常用的投影。(正交投影并不行,更适用于工程制图)
- 远处的物体更小,近处的物体更大
- 平行线不再平行,最后会汇聚到一个单一的点上

如图所示,平行的铁轨在透视投影的情况下,最终铁规会汇聚到一个点上。
在学习透视投影之前,要先了解一些知识:齐次坐标的属性!
- (x,y,z,1),(kx,ky,kz,k!=0),(xz,yz,z^2,z!=0),全都代表了同一个(x,y,z)点。齐次坐标(x,y,z,w)所代表的点为(x/w , y/w , z/w)。
- 比如:(1,0,0,1)和(2,0,0,2) 都代表着(1,0,0)这个点。
那么如何进行透视投影?
下面有两个透视体
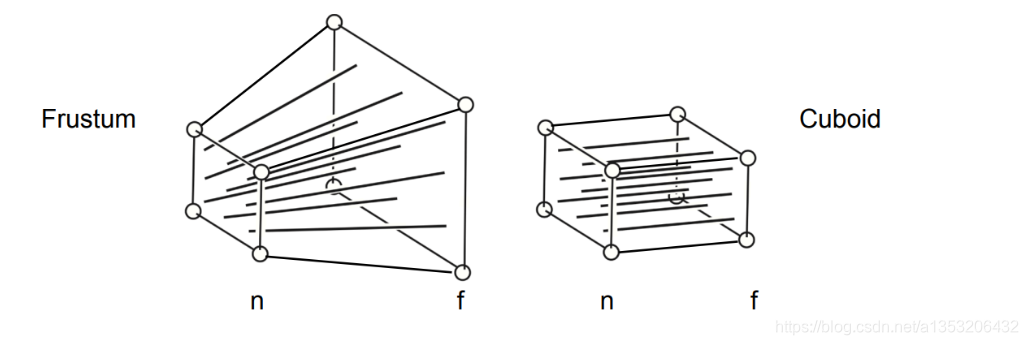
左边为透视投影的透视范围,是一个平截头体,中间的每一条线最后都会汇聚到Camera所在的位置;右边为正交(射)投影的透视范围,因为默认Camera在一个无限远的地方,所以中间的每一条线都是平行的。
要进行透视投影的话,需要完成两步
- “挤压”这个平截头体,让其成为一个长方体或者立方体,如正交(射)投影那样
- 然后对这个长方体进行正射投影,就可以得到透视投影的最终效果。
“挤压”的这种变换的实现:
所谓挤压,就是将远平面f按照比例,挤压成近平面n的那种大小,远平面f上的点的坐标就会发生变化:1.中心点不变,比如中心点为(0,0),挤压之后依旧是(0,0),2.其他的点向中心进行偏移,比如近平面是x和y在[-1,1]这个区间上的正方形 ,而远平面f为[-2,2]的正方形,那么远平面挤压过后,也要变为[-1,1]的正方形,那么远平面的点与原来的位置相比,就更靠近中心了。
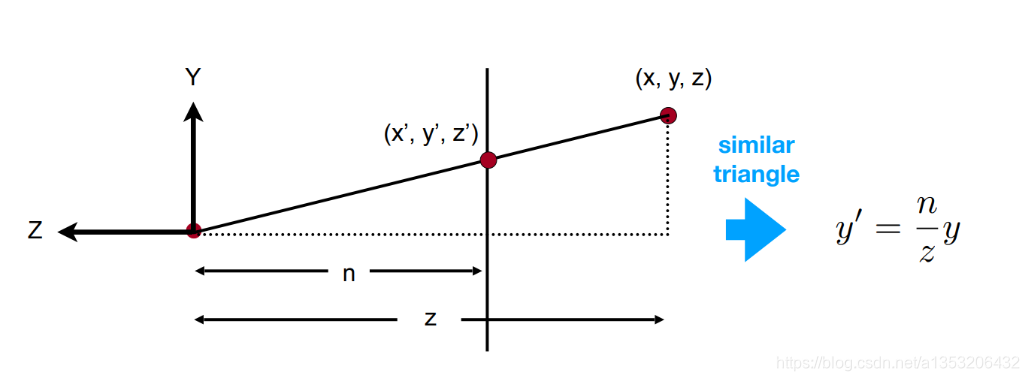
如上图所示,要用矩阵来完成这种变换就要找到这个矩阵,找到这个矩阵就意味着找到(x’ , y’ , z’)和(x , y , z)之间的关系,其中(x’ , y’ , z’)在近平面上,(x , y , z)在远平面上。由相似三角形可以得出他们之间的关系:
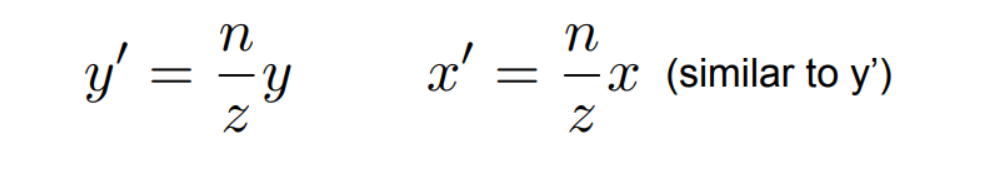
在齐次坐标下就可以表示为:
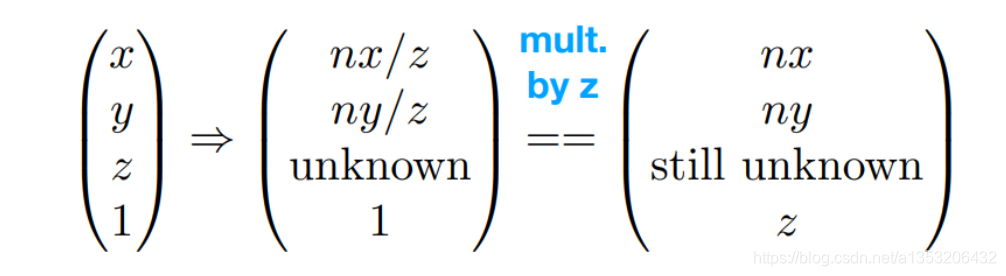
中间第二个向量表示的是(x’ ,y’ , z’),因为没有找到z和 z’ 之间的关系,所以目前用unkown来表示,然后四个维度都×z,能够得到一种比较简单的表示方法,但是代表的点仍然是原来那个点,z’仍然是unkown,但是发生了变化。
这种将透视投影“挤压”成正交投影的变换,用矩阵表示如下:
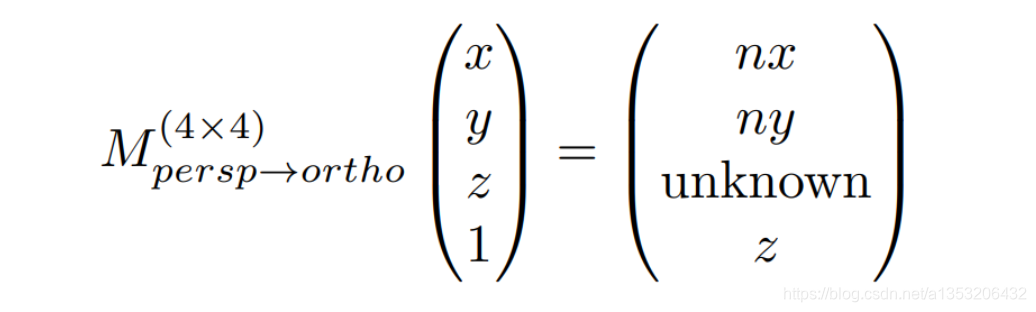
M(persp->ortho)代表着“挤压变换”,(x,y,z,1)代表原始状态下远平面上的点,(nx , ny , unkown , z)代表挤压后远平面的点。
于是,根据上面的这个式子就能够先写出矩阵的一部分信息:
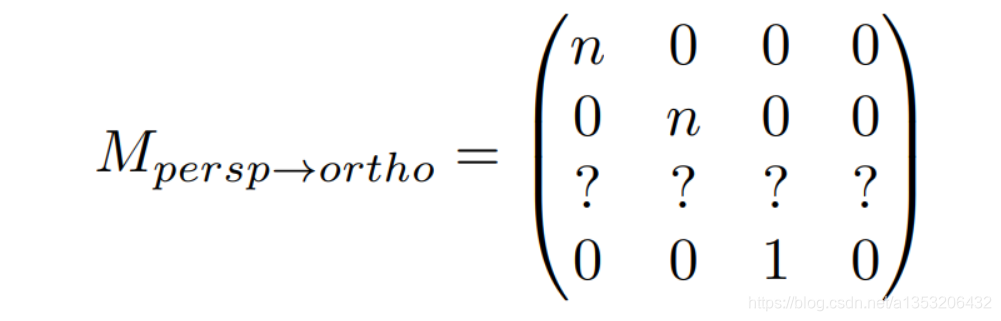
接下来的任务就是寻找第三行的数值:
第三行的值是有关于z的变换的关系,如果能找到z和 z’ 之间的关系,就能够写出第三行的数值,由观察可以得出:
- 所有近平面上的点都没有发生变换(因为所有的平面都要挤压的近平面的大小,近平面并不需要挤压,所以不发生变化)
- 所有远平面上的点的z的分量不会发生变化(因为挤压只挤压了平面的大小,并没有移动远平面的位置)
根据上述第一点,近平面点不变,可以得到:

因为近平面的点不变,所以输入的点和输出的点应该是相等的,同一个点
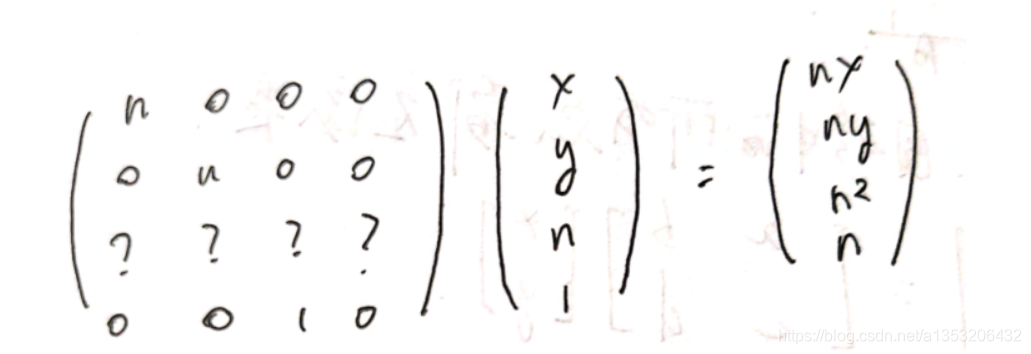
由这个式子可以得出:第三行必定是为(0,0,A , B)的格式,并且
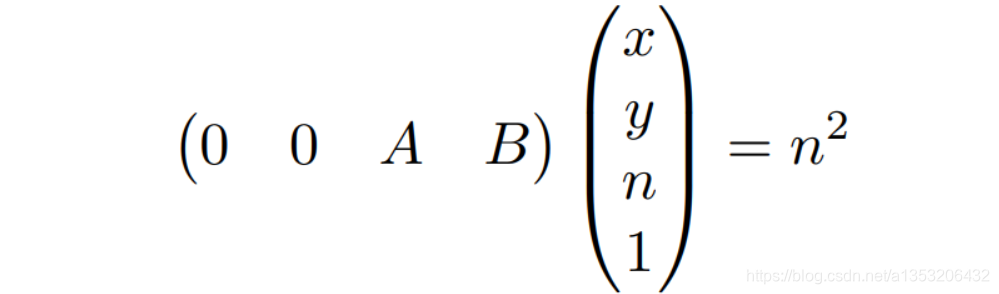
进一步推到得到:
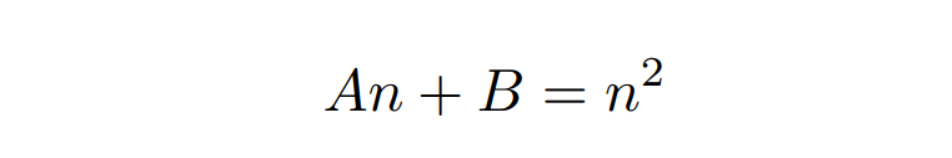
然后再利用上述的第二点:在远平面上的任何点的z值都不会发生变换,比如选一远平面上的点为(0,0,f,1),则:
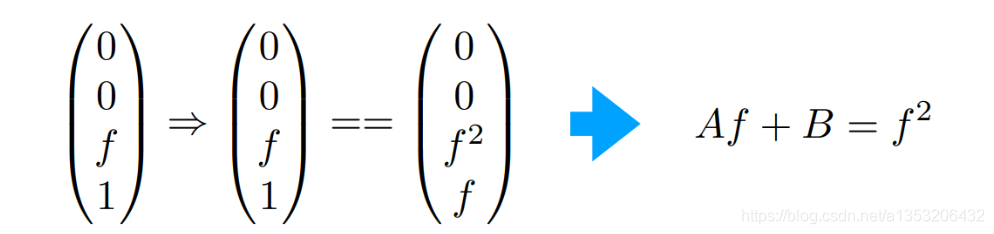
根据两个等式,就可以求A和B的值:

最后就能够获得”挤压变换“的矩阵
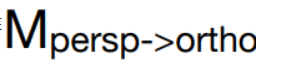
接下来应该做什么?
- 先做正射投影
- 透视投影的变换就是正射投影和挤压变换的叠加:
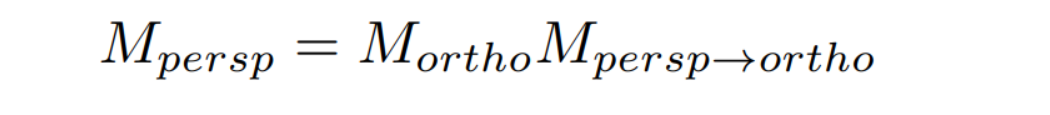
这篇关于GAMES101-现代计算机图形学入门-闫令琪 - lecture4 观测变换(viewing transformation) - 课后笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







