本文主要是介绍Two are Better than One Joint Entity and Relation Extraction with Table-Sequence Encoders,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

Two are Better than One: Joint Entity and Relation Extraction with Table-Sequence Encoders
两个都比一个好:表序编码器的联合实体和关系提取
code
Abstract
对于联合实体关系抽取,许多研究者将联合任务归结为一个填表问题,他们主要专注于学习单个编码器来捕获同一空间内的两个任务所需的信息(一个表抽取实体和关系)。作者认为设计两个不同的编码器捕获这两种不同类型的信息更好,因此本文提出了一种新颖的Table-Sequence编码器,其中两个不同的编码器(Table和序列编码器)被设计成在表示学习过程中相互帮助,本文并证明了两个编码器比一个更有优势。仍然使用表格结构,引入BERT中的attention权重进行表格中元素表示的学习。
1 Introduction
在几种联合抽取的方法中,将NER和RE转化为一个填表问题,对于形成的2D表,表中每个条目捕获句子内两个独立单词的交互,NER任务再被转化为一个序列标签问题,即对角线的条目是标签,而RE被认为是标签表内其他条目的问题;这种方法将NER和RE整合到一个表格中,实现了两个任务之间的潜在有用的交互。
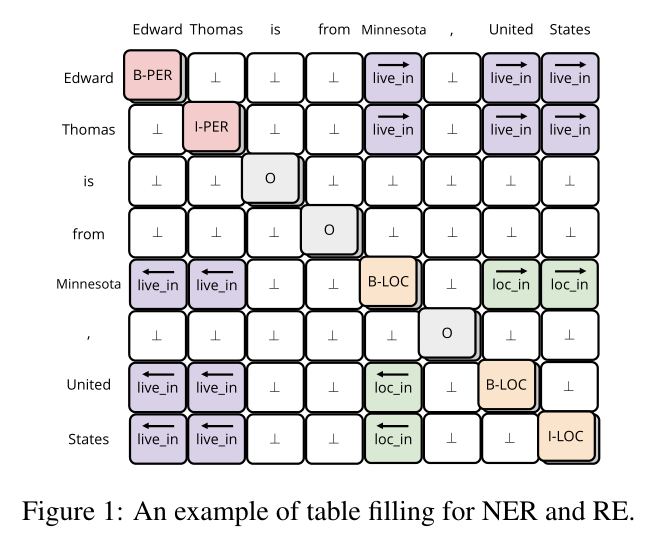
作者认为一张表解决两个问题可能会受到特征混淆的影响(一个任务提取的特征可能与另一个任务的特征一致或冲突,从而导致学习模型变得混乱),其次这种结构没有充分利用到表结构,因为这种方法仍然是将表结构转化为序列,然后使用序列标签方法填表,因此在转化期间2D表中的关键结构信息可能会丢失(图1左下角共享相同的标签)。
针对以上问题,本文提出一种新的方法解决上述限制。使用两种不同的结构(序列表示和表表示)单独表示NER和RE;
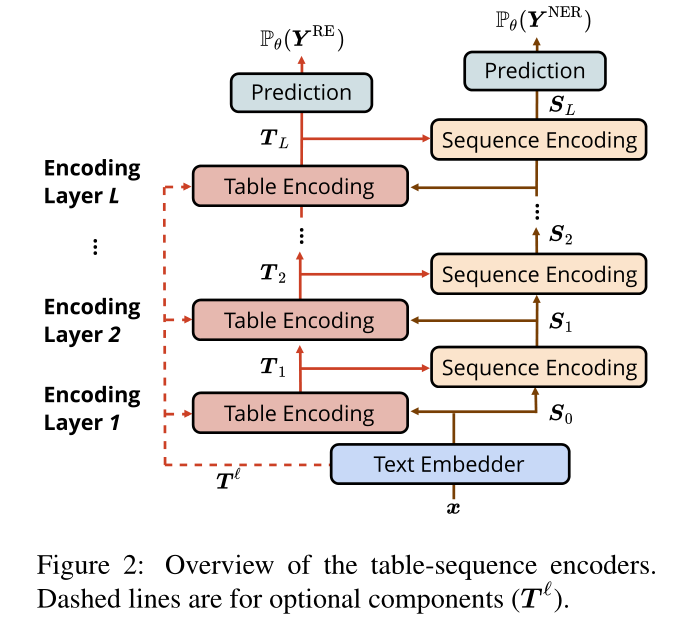
通过这种结构不仅可以将这两个单独的表示用于捕获特定于任务的信息,而且作者设计了一种机制使两个子任务进行交互,以便利用NER和RE任务背后的内在联系。
2 Model
2.1 Problem Formulation
NER看做序列标注问题,其中gold entity tags y N E R y^{NER} yNER是BIO;RE看做表格填充任务
形式上,给定输入句子 x = [ x i ] 1 ≤ i ≤ N x=[x_i]_{1\le i\le N} x=[xi]1≤i≤N,维护标签表: y R E = [ y i , j R E ] i ≤ i , j ≤ N y^{RE}=[y^{RE}_{i,j}]_{i\le i,j \le N} yRE=[yi,jRE]i≤i,j≤N
假设从mention x i b , . . . , x i e x_{i^b},...,x_{i^e} xib,...,xie到mention x j b , . . . , x j e x_{j^b},...,x_{j^e} xjb,...,xje 有关系r,则:
y i , j R E = r → y i , j R E = r ← y_{i,j}^{RE}=\overrightarrow{r}\\ y_{i,j}^{RE}=\overleftarrow{r} yi,jRE=ryi,jRE=r
其中 i ∈ [ i b , i e ] ∧ j ∈ [ j b , j e ] i\in [i^b,i^e]\wedge j\in[j^b,j^e] i∈[ib,ie]∧j∈[jb,je], ⊥ \bot ⊥表示没有关系的单词对
表3显示了两个编码器在每一层的详细信息,以及如何交互
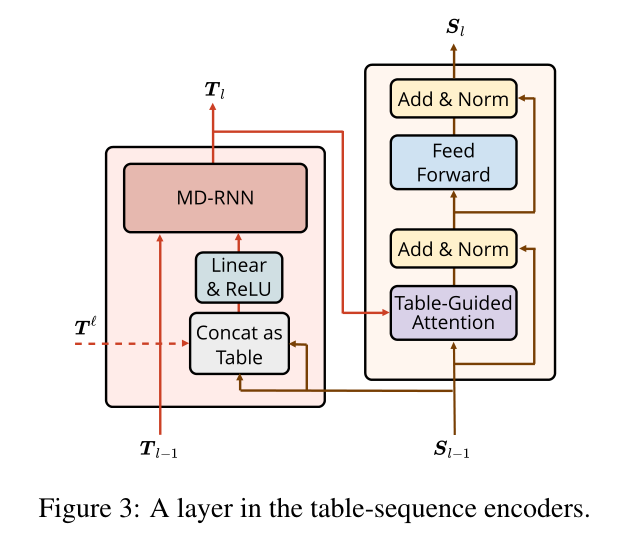
在每一层中,表编码器使用序列表示法来构造表表示法,然后序列编码器使用表表示法来对序列表示法进行上下文处理。
2.2 Text Embedder
对于包含N个单词 x = [ x i ] 1 ≤ i ≤ N x=[x_i]_{1\le i \le N} x=[xi]1≤i≤N的句子,其中单词嵌入为: x w ∈ R N × d 1 x^w\in \mathbb{R}^{N\times d_1} xw∈RN×d1,LSTM计算的字符嵌入为: x c ∈ R N × d 2 x^c\in \mathbb{R}^{N\times d_2} xc∈RN×d2,由BERT产生的上下文单词嵌入: x l ∈ R N × d 3 x^l\in \mathbb{R}^{N\times d_3} xl∈RN×d3
将三个特征向量进行拼接,并使用linear来形成初始序列表示 S 0 ∈ R N × H S_0\in \mathbb{R}^{N\times H} S0∈RN×H:
S 0 = L i n e a r ( [ x c ; x w ; x l ] ) S_0=Linear([x^c;x^w;x^l]) S0=Linear([xc;xw;xl])
2.3 Table Encoder
图3左侧所示的表格编码器是用于学习表格表示(N×N个向量表格)的神经网络,其中第i行和第j列的向量对应于输入句子的第i和第j个单词。本文首先通过将序列表示的两个向量进行连接,然后是通过一个全连接层来构建一个非上下文表,以将隐藏大小减半。
形式化上,对于第l层(表表示和序列表示交互的第l层),有 X l ∈ R N × N × H X_l\in \mathbb{R}^{N\times N\times H} Xl∈RN×N×H:
X l , i , j = R e L U ( L i n e a r ( [ S l − 1 , i ; S l − 1 , j ] ) ) X_{l,i,j}=ReLU(Linear([S_{l-1,i};S_{l-1,j}])) Xl,i,j=ReLU(Linear([Sl−1,i;Sl−1,j]))
接下来使用GRU的多维递归神经网络来对 X l X_l Xl进行上下文处理,迭代计算每个单元格的隐藏状态以形成上下文化的表格表示 T l T_l Tl,其中:
T l , i , j = G R U ( X l , i , j , T l − 1 , i , j , T l , i − 1 , j , T l , i , j − 1 ) T_{l,i,j}=GRU(X_{l,i,j},T_{l-1,i,j},T_{l,i-1,j},T_{l,i,j-1}) Tl,i,j=GRU(Xl,i,j,Tl−1,i,j,Tl,i−1,j,Tl,i,j−1)
多维GRU通常沿着层、行和列的维度利用上下文,也就是说不仅考虑到了相邻行和列的单元格,还考虑上一层的单元格。对于表格法来说,句子长度为N,那么时间复杂度就变成了 O N × N O^{N\times N} ON×N,对角线条目的计算可以同时计算(将对角线条目定义为位置(i,j)处的偏移),然后通过并行化进行优化,将复杂度降低到 O N O^N ON。
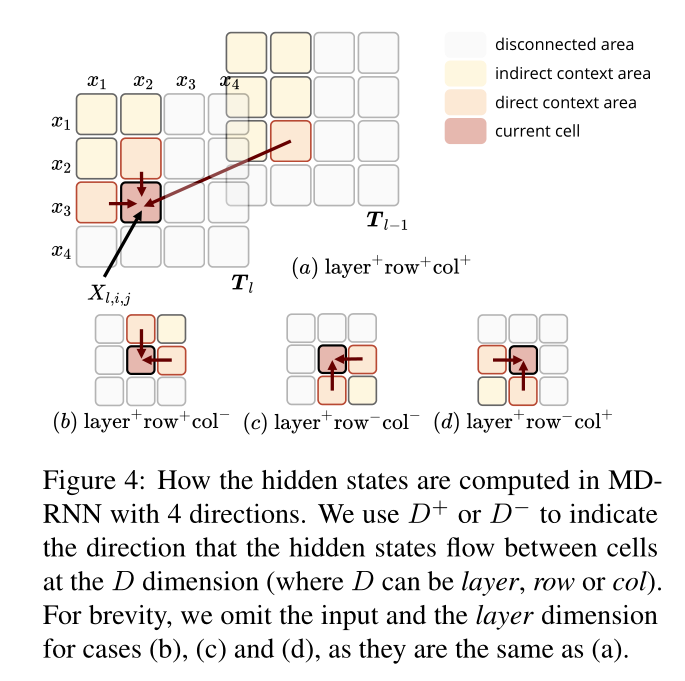
由图4直观上可以看到,让网络能够全方位的方位周围环境能提高性能,因此需要4个RNN来完成这个工作,从4个方向上访问上下文以对2D表进行建模,然而作者经验上发现只考虑情况a和c的设置效果与四种情况全部考虑所得到的的性能差不多,因此为了减少计算量,作者使用了两个方向,最终的表格表示是两个RNN的隐藏状态的串联:
T l , i , j ( a ) = G R U ( a ) ( X l , i , j , T l − 1 , i , j ( a ) , T l , i − 1 , j ( a ) , T l , i , j − 1 ( a ) ) T l , i , j ( c ) = G R U ( c ) ( X l , i , j , T l − 1 , i , j ( c ) , T l , i + 1 , j ( c ) , T l , i , j + 1 ( c ) ) T l , i , j = [ T l , i , j ( a ) , T l , i , j ( c ) ] T_{l,i,j}^{(a)}=GRU^{(a)}(X_{l,i,j},T^{(a)}_{l-1,i,j},T^{(a)}_{l,i-1,j},T^{(a)}_{l,i,j-1})\\ T_{l,i,j}^{(c)}=GRU^{(c)}(X_{l,i,j},T^{(c)}_{l-1,i,j},T^{(c)}_{l,i+1,j},T^{(c)}_{l,i,j+1})\\ T_{l,i,j}=[T_{l,i,j}^{(a)},T_{l,i,j}^{(c)}] Tl,i,j(a)=GRU(a)(Xl,i,j,Tl−1,i,j(a),Tl,i−1,j(a),Tl,i,j−1(a))Tl,i,j(c)=GRU(c)(Xl,i,j,Tl−1,i,j(c),Tl,i+1,j(c),Tl,i,j+1(c))Tl,i,j=[Tl,i,j(a),Tl,i,j(c)]
2.4 Sequence Encoder
通过Sequence Encoder学习序列表示(a sequence of vectors),其中第i个向量表示输入句子中的第i个单词,该结构类似于transformer结构,见图3的右半部分,本文用表格引导注意力(Table-Guided Attention)取代按比例缩放的点积注意力。

通用注意力的计算过程如下:
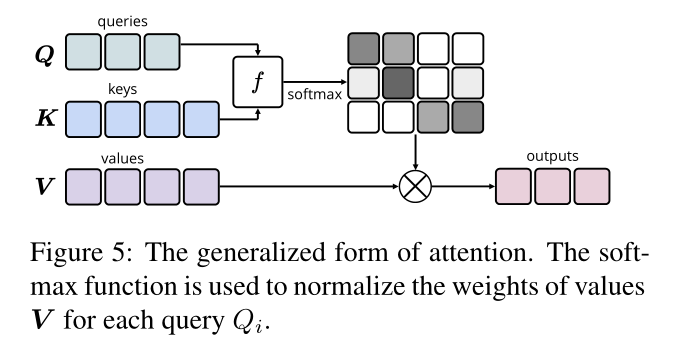
对于每个query,输出是这些值的加权和,其中分配给每个value的权重由query与所有key的相关性确定:
f ( Q i , K j ) = U ⋅ g ( Q i , K j ) g ( Q i , K j ) = t a n h ( Q i W 0 + K j W 1 ) f(Q_i,K_j)=U\cdot g(Q_i,K_j)\\ g(Q_i,K_j)=tanh(Q_iW_0+K_jW_1) f(Qi,Kj)=U⋅g(Qi,Kj)g(Qi,Kj)=tanh(QiW0+KjW1)
其中U是可学习向量,g是将每个query-key pair 映射到向量的函数,图5中f的输出即是query-key pair构造的注意力权重。
本文的表格引导注意力中,输入即是上一层的序列表示 S l − 1 S_{l-1} Sl−1,表格引导注意力是自注意力,注意力的得分函数f为:
T l , i , j = g ( S l − 1 , i , S l − 1 , j ) = g ( Q i , K j ) f ( Q i , K j ) = U ⋅ T l , i , j T_{l,i,j}=g(S_{l-1,i},S_{l-1,j})=g(Q_i,K_j)\\ f(Q_i,K_j)=U\cdot T_{l,i,j} Tl,i,j=g(Sl−1,i,Sl−1,j)=g(Qi,Kj)f(Qi,Kj)=U⋅Tl,i,j
表格引导注意力的优点:1.不比计算g函数,因为 T l T_l Tl已经从表编码器中获得(2) T l T_l Tl是沿行、列和层维度的上下文得到的表征,分别对应于query、key、value,这样的上下文信息使网络能够更好的捕获更难的word-word依存关系(3)并且允许表编码器参与学习过程,从而形成两个编码器之间的双向交互。序列编码器的其余部件类似于transformer,对于 l l l层,在自注意力之后使用前馈神经网络FFNN,并使用残差连接和层标准化得到以获取输出序列表示:
S l ∼ = L a y e r N o r m ( S l − 1 + S e l f A t t n ( S l − 1 ) ) S l = L a y e r N o r m ( S l ∼ + F F N N ( S l ∼ ) \overset{\sim}{S_l}=LayerNorm(S_{l-1}+SelfAttn(S_{l-1}))\\ S_l=LayerNorm(\overset{\sim}{S_l}+FFNN(\overset{\sim}{S_l}) Sl∼=LayerNorm(Sl−1+SelfAttn(Sl−1))Sl=LayerNorm(Sl∼+FFNN(Sl∼)
2.5 Exploit Pre-trained Attention Weights
图2、3中的虚线来自预训练模型BERT的注意力权重形式的信息,本文将所有头部和所有层的注意力进行叠加,形成 T l ∈ R N × N × ( L l × A l ) T^{l}\in \mathbb{R}^{N\times N \times (L^l\times A^l)} Tl∈RN×N×(Ll×Al),其中 L l L^l Ll是transformer的层数, A l A^l Al是每层中head的数量,本文利用 T l T^l Tl在表编码器中形成MD-RNN的输入,section2.3中的公式1被替换成:
X l , i , j = R e L U ( L i n e a r ( [ S l − 1 ; s l − 1 ; T i , j l ] ) ) X_{l,i,j}=ReLU(Linear([S_{l-1};s_{l-1};T_{i,j}^l])) Xl,i,j=ReLU(Linear([Sl−1;sl−1;Ti,jl]))
2.6 Traning and Evaluation
本文使用 S L S_L SL和 T L T_L TL来预测实体标签和关系标签的概率分布:
P θ ( Y N E R ) = s o f t m a x ( L i n e a r ( S L ) ) P θ ( Y R E ) = s o f t m a x ( L i n e a r ( T L ) ) P_\theta(Y^{NER})=softmax(Linear(S_L))\\ P_\theta(Y^{RE})=softmax(Linear(T_L)) Pθ(YNER)=softmax(Linear(SL))Pθ(YRE)=softmax(Linear(TL))
其中 Y N E R 、 Y R E Y^{NER}、Y^{RE} YNER、YRE是预测标签的随机变量, P θ P_\theta Pθ是概率估计函数, θ \theta θ是模型参数
采用交叉熵计算损失:
L N E R = ∑ i ∈ [ 1 , N ] − l o g P θ P θ ( Y i N E R = y i N E R ) L R E = ∑ i , j ∈ [ 1 , N ] ; i ≠ j − l o g P θ P θ ( Y i R E = y i R E ) \mathcal{L}^{NER}=\sum_{i\in [1,N]}-logP_\theta P_\theta (Y_i^{NER}=y_i^{NER})\\ \mathcal{L}^{RE}=\sum_{i,j\in [1,N];i\ne j}-logP_\theta P_\theta (Y_i^{RE}=y_i^{RE}) LNER=i∈[1,N]∑−logPθPθ(YiNER=yiNER)LRE=i,j∈[1,N];i=j∑−logPθPθ(YiRE=yiRE)
其中, y N E R y^{NER} yNER和 y R E y^{RE} yRE是gold tag,目标函数是: L N E R + L R E L_{NER}+L_{RE} LNER+LRE
在评估过程中,关系的预测依赖于实体的预测,因此首先预测实测,然后查找关系概率表 P θ ( Y R E ) P_\theta(Y^{RE}) Pθ(YRE),查看预测的实体之间是否存在有效的关系,具体地说,通过选择概率最高的类别来预测每个单词的实体tag:
a r g m a x e P θ ( Y i N E R = e ) \underset{e}{argmax}P_\theta(Y_i^{NER}=e) eargmaxPθ(YiNER=e)
整个tag序列可以被转换成具有其边界和类型的实体。对于给定的两个实体span : ( i b , i e ) 和 ( j b , j e ) (i_b,i_e)和(j_b,j_e) (ib,ie)和(jb,je),其关系由下式给出:
a r g m a x r → ∑ i ∈ [ i b , i e ] , j ∈ [ j b , j e ] P θ ( Y i , j R E = r → ) + P θ ( Y j , i R E = r ← ) \underset{\overrightarrow{r}}{argmax}\sum_{i\in [i^b,i^e],j\in [j^b,j^e]}P_\theta(Y_{i,j}^{RE}=\overset{}{\overrightarrow{r}})+P_\theta(Y_{j,i}^{RE}=\overset{}{\overleftarrow{r}}) rargmaxi∈[ib,ie],j∈[jb,je]∑Pθ(Yi,jRE=r)+Pθ(Yj,iRE=r)
其中 ⊥ \bot ⊥表示没有无关系
3 Experiments
3.1 Model Step
根据ACE05验证集调参,其他数据集使用相同的设置,Glove用于初始化词嵌入,BERT使用默认的参数,堆叠了三层具有独立参数的编码层(图2,每层中包含GRU单元),对于表编码器,使用两个独立的MD-RNN;对于序列编码器,使用8-head注意力表示,结果如下:
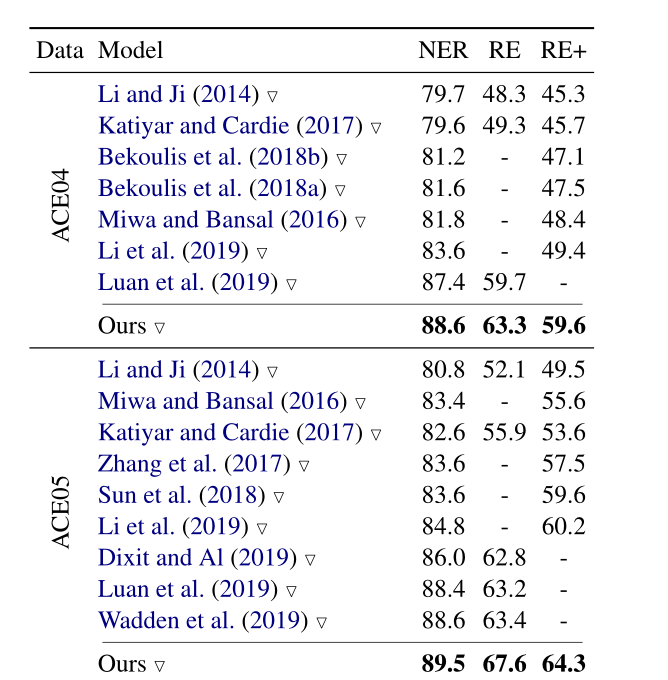
4 启示
- 论文是写的真的好,表达能力很强
- transformer框架的部分应用可以在其他地方使用
- 还是老生常谈的需要占用很多显存
- 表表示和序列表示的交互策略可以尝试修改成其他解码方式并实现交互
这篇关于Two are Better than One Joint Entity and Relation Extraction with Table-Sequence Encoders的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





