OLAK: An Efficient Algorithm to Prevent Unraveling in Social Networks

作者 Fan Zhang†, Wenjie Zhang§, Ying Zhang†, Lu Qin†, Xuemin Lin§

摘要

为了防止用户的离开，造成图网络的分解，所以通过激励一些用户，影响周围的顶点，起到增强网络的作用。那么应该激励哪些用户呢，最简单的办法就是选中一个顶点，查看最网络起的作用，依次查看所有的顶点，但是这样很浪费时间。所以发明了一种类似于洋葱层的算法，大大减少搜索空间，提高效率。

1、介绍

说白了，就是固定一些顶点从而扩大kcore。研究表明k>=3 锚定kcore是一个NP难问题。
**挑战：**为了避免枚举大小为b的所有可能锚集，采用贪婪试探法。通过计算每个可能锚点的k核，在每次迭代中计算最佳锚集。原因有两方面。(1)候选锚的数量较多。很明显，我们不需要锚定图的k-core中的顶点。然而，剩余顶点的数量仍然很大。(2)虽然k-core的计算时间在边数上是线性的，但在候选锚点数量较多的情况下，代价比较昂贵。
**解决：**设计了一个辅助结构L，称为洋葱层(onion layers)，以保持一个小的顶点集，并开发相应的高效技术，显著减少搜索空间。由于锚点的存在，会有一些新的顶点加入k-core，本文称之为follower。采用了贪婪启发式，我们的研究重点是在图中寻找最佳锚点，即follower数量最多的顶点。当我们只考虑一个锚点时，所有的追随者必须驻留在(k-1)-shell，即(k-1)-core中的顶点，而不是k-core中的顶点。我们把这些顶点和它们的邻居放到洋葱层里，并证明我们只需要将L中的顶点作为候选锚点来寻找最佳锚点。证明了在计算过程中只需要考虑L中的顶点，这大大减少了搜索空间。

2、前提

定义一： kcore
定义二： kshell，Sk(G) = Ck(G) \ Ck+1(G).
定义三： anchored k-core,Ck(GA),如果增加锚定顶点，kcore中新增加的顶点叫跟随者。
问题描述：找到一组顶点A，使kcore的规模最大，当k≥3时，锚定k核问题为NP-hard，不存在非平凡多项式算法k>2，采取贪婪算法。启发式算法，施加洋葱层结构。

3、过程

基于洋葱层的锚定内核(OLAK)算法可以有效、高效地为锚定k核问题找到一组锚。
创造一个洋葱层L，候选锚点和跟随者在L里查找。
G的洋葱层(用L表示)由(k-1)-shell中的顶点及其不属于k-core的邻居组成;即L:= Sk−1(G)∪{NB(Sk−1(G)，G) \Ck(G)}。

3.2

定理一：跟随者只能在Sk−1(G)。
定理二：给定一个图G，如果一个锚定顶点x至少有一个跟随者，则x来自L

3.3

计算跟随着，(1)先计算出没有锚定时的kcore，再计算锚定时的kcore，然后作差，就是followe.(2) 由kcore 往外扩展

3.3.1、洋葱层

定理三:对于kcore的计算，无论什么删除顺序，kcore都是一样的
洋葱层：L consists of s+1 layers, {L0, L1, . . ., Ls} (Ls0 = L)。Then we put the neighbors of Sk−1(G)(excluding the ones in Ck(G) and Ls1) to L0

3.3.2 基于洋葱层的跟随者计算

(1)寻找候选follower，为锚点x探索候选follower;(2)提前终止，在计算过程中递归地丢弃没有希望的候选项。
**定义四：**支持路径
given anchor vertex x if there is a path x -> u such that all vertices are from Ls
1 and we have l(y) < l(z) for every two consecutive vertices y and z along this path.
定理四：如果一个顶点u是锚定x的跟随者，则有支持路径x->u
（2）提前终止搜索，在洋葱层的顶点有三种状态，未被访问、被访问且满足要求、被抛弃。
degree upper bound d+(u) 度上界约束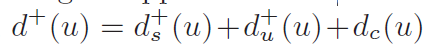

**定理五：**一个洋葱层顶点不可能成为跟随者如果$$d^{+}(u)<k$$
(3) 查找跟随者

3.4 、OLAK

将介绍两种剪枝技术，以进一步减少候选锚的数量。在此基础上，提出了OLAK算法来寻找图中的最佳锚点，并展示如何处理使用多个锚的情况。

3.4.1 跟随者

**定理六：**如果一个一个锚点是另一个锚点的跟随者，则他不能成为锚点。Given two vertices x and u in L, we have |F(x)| > |F(u)| if u ∈ F(x).

3.4.2 上界剪枝，确定最好的锚点

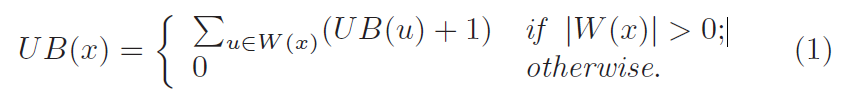
**定理七：**Let λ denote the number of followers of the best anchor seen so far. We can exclude any candidate anchor，x if UB(x) < λ.

3.4.3

说明：本文章对这篇论文都是自己的理解，如果不对请提出