本文主要是介绍论文阅读Unraveling traveler mobility patterns and predicting user behavior in the Shenzhen metro system,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这篇论文主要是对地铁出行者的出行模式进行分析,然后借助entropy来对出行者的出行规律性进行度量,在此基础上根据entropy将出行者划分为三类,并分别用马尔科夫链和HMM模型进行预测分析。
1.entropy计算
作者使用entropy来进行出行规律性的度量,在此之前,需要进行一些预先的处理。对于出行者的出行时空特性,需要进行离散化表达,因为entropy的计算需要离散的值。
对于出行者的空间特性,基于地铁刷卡数据挖掘出出行者最频繁出现的站点和第二频繁出行的站点,这两个站点一般而言就是出行者的家和工作地。所有其他站点都设置为其他。最频繁出现的站点标记为1,第二频繁出现的站点标记为2,其他所有站点都标记为3。
对于出行者的时间特性,作者将一天划分为四个时间段,分别是早上、下午、傍晚和夜间,morning (6 a.m. to 11 a.m.), afternoon (11 a.m. to 4 p.m.), evening(4 p.m. to 8 p.m.) and night (8 p.m. to 12 p.m.)。
作者使用一个三元组作为一个item,三元组的表示为{s1,s2,y},其中s1是入站、s2是出站,y是时间。因此的话所有item项目的可能性为:[(1, 2,M),(1, 3,M),(2, 1,M),(2, 3,M), (3, 1,M),(3, 2,M),(3, 3,M),(1, 2,A),(1, 3,A),(2, 1,A),(2, 3,A),(3, 1,A),(3, 2,A),(3, 3,A),
(1, 2,E),(1, 3,E),(2, 1,E),(2, 3,E),(3, 1,E),(3, 2,E),(3, 3,E),(1, 2,N),(1, 3,N),(2, 1,N),(2,3,N),(3,1,N),(3, 2,N),(3, 3,N)]。
成功对每一位出行者的出行序列进行表示后,使用下式进行entropy的计算。其中x代表空间位置变量,y代表时间变量。P(x,y)代表x和y的联合概率,也就是一个特定用户在时间y出现在位置x的频率。
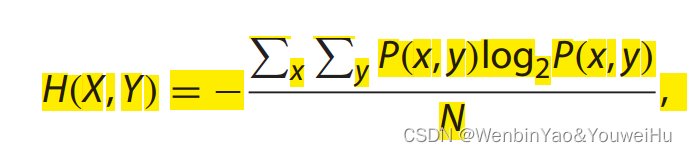
计算得到entropy之后,使用kmeans算法将出行者聚类成若干类,在这个研究中,出行者被聚成3类,分别是规律出行者、不规律出行者和可变出行者。
2.出行模式预测
作者在文章中还给出了两种出行模式预测方法,第一种是Markov model,第二种是hidden Markov model,但是由于这并非是我关注的重点,对该部分感兴趣的读者可以详细阅读该文章的后半部分。
3.参考文献
Yang, C. , Yan, F. , & Ukkusuri, S. V. . Unraveling traveler mobility patterns and predicting user behavior in the shenzhen metro system. Transportmetrica.
这篇关于论文阅读Unraveling traveler mobility patterns and predicting user behavior in the Shenzhen metro system的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








