【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换

本文主要是介绍【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

理论恒叨系列

【理论恒叨】【立体匹配系列】经典SGM：（1）匹配代价计算之互信息（MI）
【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换
【理论恒叨】【立体匹配系列】经典SGM：（3）代价聚合（Cost Aggregation）
【理论恒叨】【立体匹配系列】经典SGM：（4）视差计算、视差优化

  上篇博客中，我们介绍了基于互信息的代价计算方法，由于基于互信息的匹配代价计算由于需要初始视差值，所以需要通过分层迭代的方式得到较为准确的匹配代价值，而且概率分布计算稍显复杂，这导致代价计算的效率并不高。学者Zabih和Woodfill ¹ 提出的基于Census变换法也被广泛用于匹配代价计算。Census变换是使用像素邻域内的局部灰度差异将像素灰度转换为比特串，思路非常简单，通过将邻域窗口（窗口大小为$n\times m$，$n$和$m$都为奇数）内的像素灰度值与窗口中心像素的灰度值进行比较，将比较得到的布尔值映射到一个比特串中，最后用比特串的值作为中心像素的Census变换值$C_s$，如公式1所示：

式1

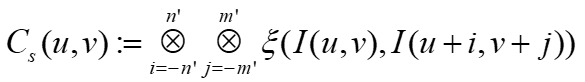
其中，$n^{\prime }$和$m^{\prime }$分别为不大于$n$和$m$的一半的最大整数，$\oplus$为比特位的逐位连接运算，$\xi$运算则由公式2定义：

式2

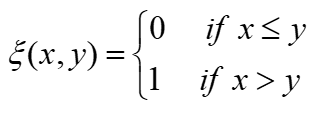
基于Census变换的匹配代价计算方法是计算左右影像对应的两个像素的Census变换值的汉明（Hamming）距离，即

式3

  Hamming距离即两个比特串的对应位不相同的数量，计算方法为将两个比特串进行亦或运算，再统计亦或运算结果的比特位中不为1的个数。

  基于Census变换的匹配代价计算方法如图1所示，

图1 汉明距离示意图

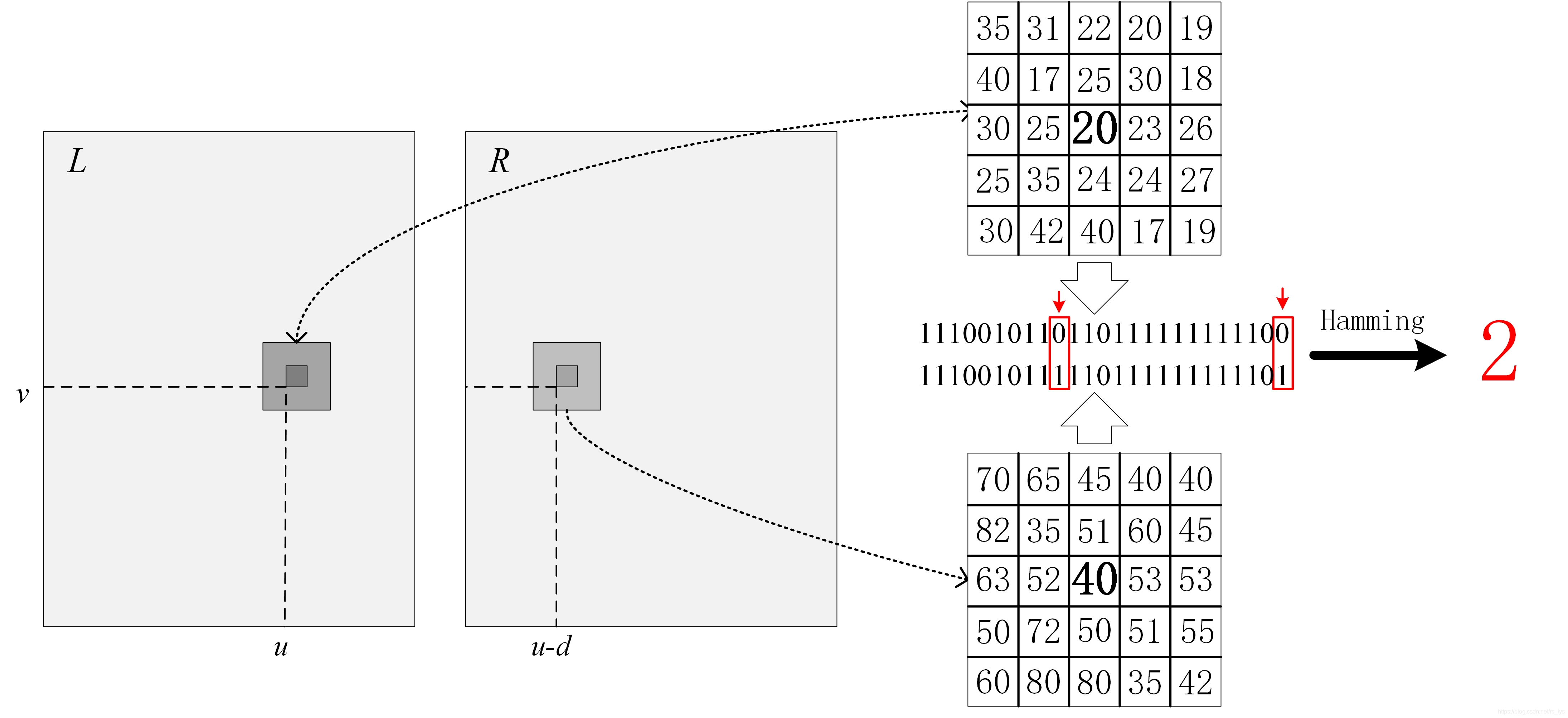
  从图1可以看出，Census变换对整体的明暗变化并不敏感，因为是比较的相对灰度关系，所以即使左右影像亮度不一致，也能得到较好的匹配效果。

  Census相比互信息还具有并行度高的优点，因为Census变换值是局部窗口运算，所以每个像素可以独立运算，这个特性让其可以很好的设计多线程并行计算模型，无论是CPU并行还是GPU并行都能达到非常高的并行效率。

  在实际匹配过程中，简单的执行匹配代价计算并不能得到高质量的视差图，必须经过代价聚合步骤，聚合后的代价能够更准确地反应匹配相似度，下篇博客中，将为大家详解SGM的代价聚合步骤，查看请点击 >> link

附：
计算Census值及Hamming的代码：
Census值：

uint8 gray_center= img_data[image_y *img_width + image_x];		// 中心像素值
// 遍历大小为2csh*2csw的窗口内邻域像素，逐一比较像素值与中心像素值的的大小，计算census值
uint32 census_value = 0u;
for (sint32 i = -csh; i <= csh; i++) {for (sint32 j = -csw; j <= csw; j++) {census_value <<= 1;uint8 gray = img_data[(image_y + i)*img_width + image_x + j];if (gray < gray_center) {census_value += 1;}}
}
census[image_y *img_width + image_x] = census_value;		// 中心像素的census值

Hamming距离：

// unsigned to 32bit
//计算hamming距离
uint32 hamDist32(const uint32& x, const uint32& y)
{uint32 dist = 0, val = x ^ y;// Count the number of set bitswhile (val){++dist;val &= val - 1;}return dist;
}

码上教学系列

【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（1）框架与类设计
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（2）代价计算
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（3）代价聚合
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（4）代价聚合2
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（5）视差优化
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（6）视差填充
【恒叨立码】【码上实战】【立体匹配系列】经典SGM：（7）弱纹理优化

完整代码已发布于Github开源项目：Github/SemiGlobalMatching，欢迎免费下载

博主简介：
Ethan Li 李迎松
武汉大学 摄影测量与遥感专业博士

主方向立体匹配、三维重建

2019年获测绘科技进步一等奖（省部级）

爱三维，爱分享，爱开源
GitHub： https://github.com/ethan-li-coding
邮箱：ethan.li.whu@gmail.com

个人微信：

欢迎交流！

喜欢博主的文章不妨关注一下博主的博客，感谢！
博客主页：https://blog.csdn.net/rs_lys

---

1. ZABIH R, WOODFILL J. Non-parametric local transforms for computing visual correspondence[M]. 1994: 151-158. ↩︎

这篇关于【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---