本文主要是介绍步进电机运动八大加减速算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
引导一种模块化(Module)设计思想,将传统步进电机的控制器(controller)、驱动器(Driver)、运动算法(Arithmetic)三合一。
对比国内外步进电机驱动原理和已有工作,结合各种硬件特性,改进或实现了可实际移植并用于步进电机控制八大算法。本产品为步进电机实际控制算法实现源代码,包括市面上常用的梯形加减速算法、SPTA算法、PWM专用通道算法、特征拟合算法、任意形状的s形加减速七段法、s形logistics函数法、DMA算法、从定时器法。可用于实际项目和相关研究之用。
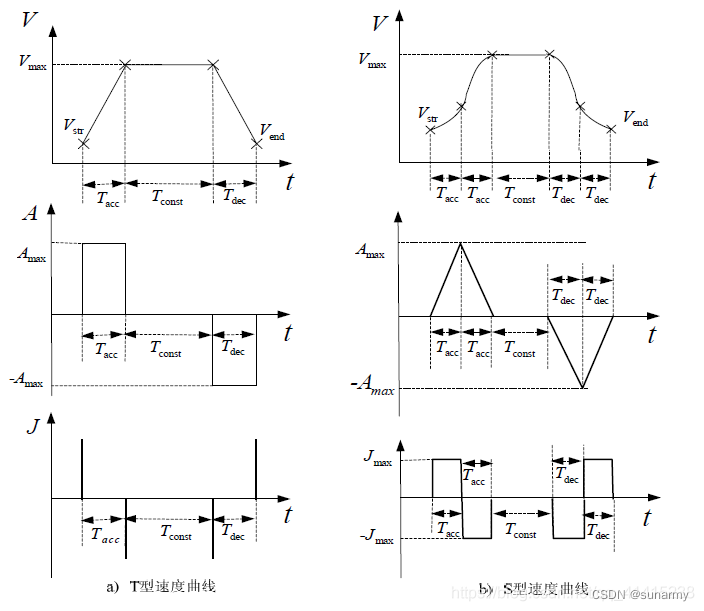
1、T梯形加减速算法
梯形算法的速度轮廓是梯形,故而得名,对梯形求导数可以得到矩形,因此本算法直接从勾勒加速度曲线入手,进行数值积分得出速度轮廓,进而转换为对应的定时器预设值,从而控制电机的速度变化,达到想要的效果。
2、SPTA算法
SPTA算法根据用户输入的加速度和速度以及总脉冲数,自动计算加减速过程所需的定时器装载值,也不需要额外的RAM来存储表格,算法效率高、灵活方便,特别适合移植到一些资源紧俏的单片机,比如51单片机等。
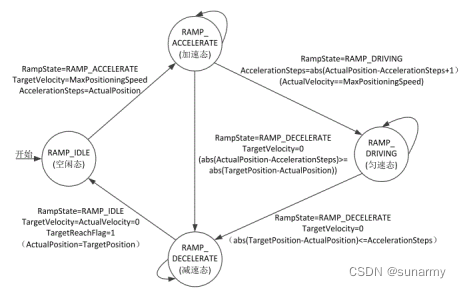
图 2-1 SpTA 控制算法状态机状态切换图
SpTA 算法同样是通过定时器来实现的,与 S 形曲线算法不同的是它没有使用定时器的 PWM 功能,仅仅是通过定时器定时中断来产生一个时间片,在定时器中断服务子程序中完成上述算法 ,在需要时,通过控制 GPIO 产生一个步进脉冲 。
SpTA 与 S 型算法的比较:
从上面的两种算法可以看出,传统的 S 形曲线控制算法实现比较简单,但是它将要输出的脉冲频率(周期)和脉冲个数存储在 RAM 里,占用了一定的内存,且要想实现更好的 控制效果, S 形曲线的 离散化程度越高,占用的 RAM 越大,如果要改变电机的运行速度曲线,需要重新计算每个阶段脉冲频率和脉冲个数,计算时使用了浮点数,运算量较大。
SpTA 算法是根据用户输入的加速度和目标速度以及设定的总脉冲数,自行决定如何输出达到最佳运动效果的脉冲,它不需要占用额外的 RAM 来存储每个阶段脉冲频率和脉冲个数,算法实现基本上都是 MCU“ 拿手 ” 的加减法和移位运算,算法效率高,但是该算法为了达到较好的运动控制,需要一个时间片很小的定时中断来调整数据,这样在输出一个脉冲期间要频繁产生中断,尤其是在电机起步和停止的时候,脉冲频率低,但是 定时器 中断的次数很高,这样 CPU 的效率就会被 定时器 中断拉低。
从算法计算量、占用 RAM 大小、控制效果和 CPU 效率上,两种控制算法对比分析如表 3.2 所示,综合考虑二者的优缺点,本系统中对于试剂盘、样本盘、反应盘等负载较大的电机使用 SpTA 控制算法,其它负载使用 S 形曲线控制算法。
表 3.2 步进电机 S 形曲线控制算法与 SpTA 控制算法比较分析
| 比较项 | S 形曲线控制算法 | SpTA 控制算法 |
| 算法计算量 | 大且使用了浮点数 | 小且使用的是整形数 |
| 占用 RAM 大小 | 较多,与控制效果相关 | 很少,与控制效果无关 |
| 控制效果 | 由离散化程度决定 | 自适应,效果较好 |
| CPU 效率 | 中断次数 = 步进数, CPU 效率较高 | 中断次数 >> 步进数, CPU 效率较低 |
3、PWM专用通道加减速算法
一般来说,采用单片机控制步进电机的方法是在定时器的中断处理函数中,对于特定的IO口进行操作来产生脉冲,这种方法的好处是灵活,可以方便的移植到各种类型的单片机,只要求该单片机具有定时器和多余的GPIO,几乎所有的单片机都能满足要求。
但是随着单片机功能的不断增强,CPU负担逐渐增多,这种方式自身缺点也逐渐显现,那就是占用了较多的计算资源。替代的办法就是采用定时器专用的PWM通道来产生所需的硬件脉冲,这样在不经常启动停止的工况下,不再需要CPU的干预,大大提高了效率。
4、特征拟合算法
该算法充分利用所选的步进电机特性曲线来选择加减速轮廓,具有非常大化电机能力的优点,而且算法占用的空间少,对于特定的步进电机具有带载能力非常大化的优点,在小负载测试中发现,使用梯形加减速算法可以在3s内完成无丢步的运动,换为该算法,可以实现2.2s无丢步加减速。
5、任意形状的S形加减速
此为S形七段法。如果从加速度轮廓上看,梯形加减速的加速度是矩形的,而且在速度切换点,加速度从正一下子变为负,会有明显的响声,因此,有必要开发更为平滑的算法。那就是S形加减速。针对S形加减速,具体做法有很多,比较简单的做法是采用sigmoid函数,一切有S形状的函数都可以拿来做基础S函数,比如log函数的变形,sin函数。不过,这些函数在S曲线的计算公式上虽然简单了,但是由于可调参数太少,导致了无法根据现实情况随意更改S曲线形尸缺少灵活性。为此,本店在理论推导的基础上推出任意形状的S形曲线算法。首先规划运动的加速度,然后积分得到速度轮廓,进而转换为步进电机的频率轮廓。
正点原子电机笔记——步进电机S形加减速 - 知乎 (zhihu.com)
【C语言】STM32控制步进电机——一种S形加减速曲线的推导与实现_步进电机s曲线加减速程序c_游楽场的博客-CSDN博客
6、S形加减速logistic函数法
S曲线常见的方法是七段法,在很多论文中都有涉及,该方法的灵活性好,可以指定任意一段加速度以及斜率。但该方法也有缺点,即在于过于灵活导致参数众多,本方法采用的logistic函数法,参数少,易于掌控。
7、DMA算法
DMA算法采用新的处理方式,只有在需要改变步进脉冲频率的时候再进入中断,这样可以提高CPU的效率,让CPU专注于执行计算密集型的工作,给任务多、计算复杂的应用提供了一种更好的解决方案。
8、从定时器法(SLAVER TIMER)
SLAVER算法是一种提升总线利用率的方法,使用两个定时器,一个输出PWM,一个工作在计数器模尸把PWM输出的同时,让计数器对其进行计数,从而释放了总线,提升了工程整体效率。
这篇关于步进电机运动八大加减速算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








