【PCL】ICP（Iterative Closest Point）原理剖析——仿射变换（Affine Transformation）数学模型

包含相同内容的两幅图像可能由于成像角度、透视关系乃至镜头自身原因所造成的几何失真而呈现出截然不同的外观，这就给观测者或是图像识别程序带来了困扰。通过适当的几何变换可以最大程度地消除这些几何失真所产生的负面影响，有利于我们在后续的处理和识别工作中将注意力集中子图像内容本身，更确切地说是图像中的对象，而不是该对象的角度和位置等。因此，几何变换常常作为其他图像处理应用的预处理步骤， 是图像归一化的核心工作之一。

1 几何变换

变换模型是指根据待匹配图像与背景图像之间几何畸变的情况，所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种：刚性变换、仿射变换、透视(投影)变换和非线性变换等，如下图：

c 和 d 的区别可以看下图：

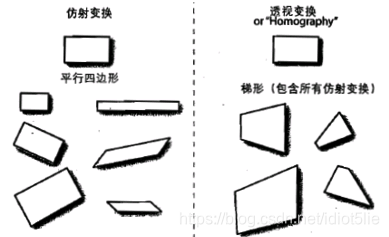
其中仿射变换就是我们本文要讨论的，而仿射变换中的平移、旋转则是刚性 ICP 的重点，本文将以二维仿射变换为例，阐述仿射变化的数学模型。

2 仿射变换

仿射变换(Affine Transformation)

Affine Transformation 是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直性”（译注：straightness，即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（译注：parallelness，其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变）。

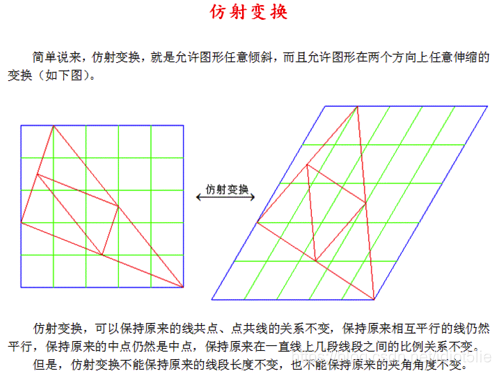
仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。

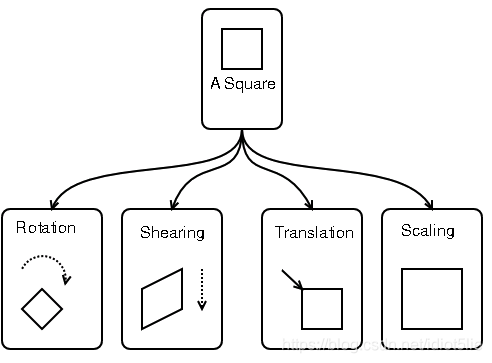
仿射变换（二维）可以用下面公式表示：

参考：图像变换的基本模型

矩阵乘法的规则如下所示：

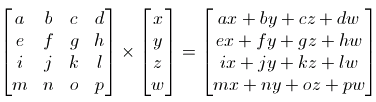
具体到二维的仿射变换的计算如下：

2.1 平移

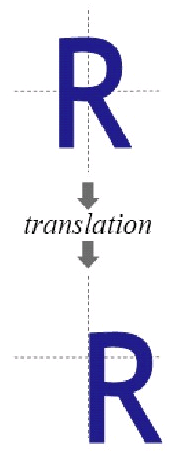
将每一点移动到 (x+tx, y+ty)，变换矩阵为：

平移变换是一种“刚体变换”，rigid-body transformation，就是不会产生形变的理想物体。

效果：

2.2 缩放

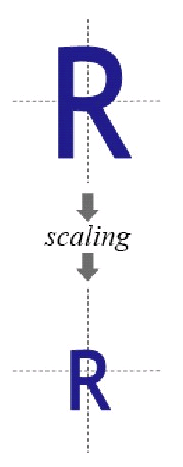
将每一点的横坐标放大（缩小）至 sx 倍，纵坐标放大（缩小）至 sy 倍，变换矩阵为：

变换效果如下：

2.3 剪切

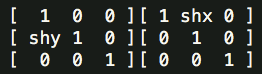
变换矩阵为：

相当于一个横向剪切与一个纵向剪切的复合：

效果：

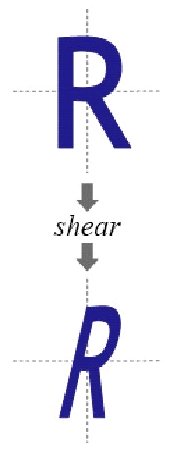
2.4 旋转

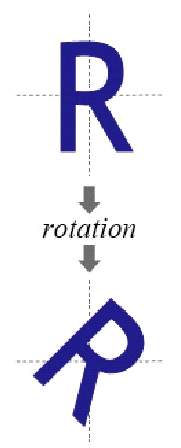
目标图形围绕原点顺时针旋转 theta 弧度，变换矩阵为：

效果：

2.5 组合

旋转变换，目标图形以 (x, y) 为轴心顺时针旋转 theta 弧度，变换矩阵为：

相当于两次平移变换与一次原点旋转变换的复合：

先移动到中心节点，然后旋转，然后再移动回去。

这个转换矩阵也可以下面这样描述：

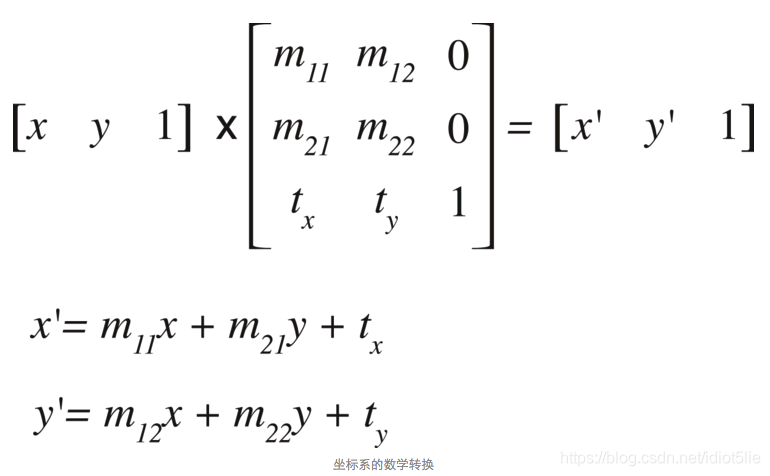
3 结论

常用转换矩阵如下：