本文主要是介绍第一门课:神经网络和深度学习(第二周)——神经网络的编程基础,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
神经网络的编程基础
- 1. 二分类
- 2. 逻辑回归
- 3. 逻辑回归的代价函数
- 4. 梯度下降法
- 5. 导数
- 6. 计算图的导数计算
- 7. 逻辑回归中的梯度下降(※)
- 8. m个样本的梯度下降
- 9. 向量化
- 10. 向量化的更多例子
- 11. 向量化 logistic 回归
- 12. 向量化 logistic 回归梯度输出
- 13. numpy 广播机制
- 14. 关于 python / numpy 向量的说明
1. 二分类
- 什么是二分类问题呢——举个栗子,给你一张图片,判断图片中动物是不是猫?
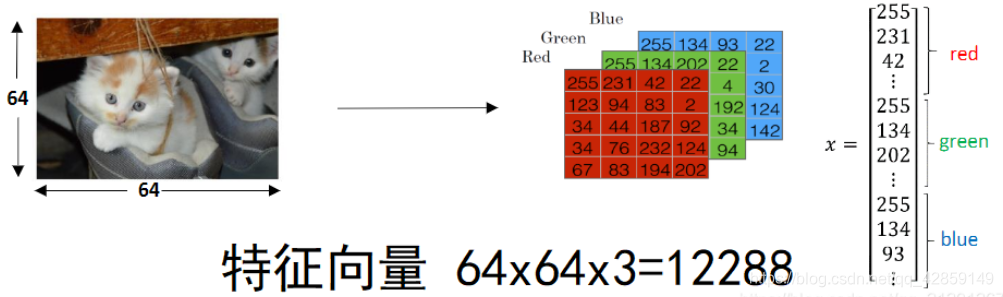
对于图像处理问题,每个图片由很多像素点组成。所以图片的特征向量是3通道的RGB矩阵,我们将其展平作为一个特征输入向量 x x x。
约定一些符号:
x x x:表示一个 n x n_x nx维数据,为输入数据,维度为( n x n_x nx,1);
y y y:表示输出结果,取值为(0,1);
( x i x^i xi, y i y^i yi):表示第 i i i 组数据,可能是训练数据,也可能是测试数据,此处默认为训练数据;
X = [ x ( 1 ) , x ( 2 ) , . . . , x ( m ) ] X=[x^{(1)},x^{(2)},...,x^{(m)}] X=[x(1),x(2),...,x(m)]:表示所有的训练数据集的输入值,放在一个 n x × m n_x×m nx×m的矩阵中,其中 m m m表示样本数目;
Y = [ y ( 1 ) , y ( 2 ) , . . . , y ( m ) ] Y=[y^{(1)},y^{(2)},...,y^{(m)}] Y=[y(1),y(2),...,y(m)]:对应表示所有训练数据集的输出值,维度为 1 × m 1×m 1×m。
2. 逻辑回归
对于二元分类问题来讲,给定一个输入特征向量 X X X,它可能对应一张图片,你想识别图片内容是否为一只猫,你需要算法能够输出预测 y ^ \hat{y} y^, y ^ \hat{y} y^ 表示 y y y 等于1的一种可能性或者是概率。
前提条件给定了输入特征 X X X, X X X是一个 n x n_x nx维的向量(相当于有 n x n_x nx个特征的特征向量)。我们用 w w w来表示逻辑回归的参数,这也是一个 n x n_x nx维向量(因为 w w w是特征权重,维度与特征向量相同),参数里面还有 b b b,这是一个表示偏差的实数。
所以给出输入 x x x以及参数 w w w和 b b b之后,我们怎样产生输出预测值 y ^ \hat{y} y^?
y ^ = w T x + b \hat{y}={{w}^{T}}x+b y^=wTx+b 这样么? 答案是否定的。
我们需要借助sigmoid函数,令 y ^ = σ ( z ) = 1 1 + e − z \hat{y}=\sigma \left( z \right)=\frac{1}{1+{{e}^{-z}}} y^=σ(z)=1+e−z1,其中 z = w T x + b z={{w}^{T}}x+b z=wTx+b。
我认为此定义原因如下:1. 为了便于解释 y ^ \hat{y} y^存在的意义,以概率形式出现更易于接受;2. 为了便于接下来代价函数的提出和理解。
3. 逻辑回归的代价函数
为了衡量一个算法在模型上的表现并以此作为优化的依据,我们需要一个代价函数。在逻辑回归中,我们需要通过训练代价函数来得到优化后的参数 w w w和参数 b b b。
Loss function: L ( y ^ , y ) = − ( y log ( y ^ ) + ( 1 − y ) log ( 1 − y ^ ) ) L\left( \hat{y},y \right)=-(y\log(\hat{y})+(1-y)\log (1-\hat{y})) L(y^,y)=−(ylog(y^)+(1−y)log(1−y^)),交叉熵损失函数,常用于二分类问题。
- 所有的样本的损失函数的平均值
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log ( y ^ ( i ) ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(\hat{y}^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-\hat{y}^{(i)}\right)\right] J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
目标就是找到合适的参数,使得代价函数最小化
4. 梯度下降法
如何寻找合适的 w , b w, b w,b 使得代价函数最小呢?
迭代的过程中,不断的在各参数的偏导数方向上更新参数值, α \alpha α 是学习率
w : = w − α ∂ J ( w , b ) ∂ w b : = b − α ∂ J ( w , b ) ∂ b \begin{aligned} &w:=w-\alpha \frac{\partial J(w, b)}{\partial w} \\ &b:=b-\alpha \frac{\partial J(w, b)}{\partial b} \end{aligned} w:=w−α∂w∂J(w,b)b:=b−α∂b∂J(w,b)
5. 导数
导数定义:函数在某一点的斜率,在不同的点,斜率可能是不同的。
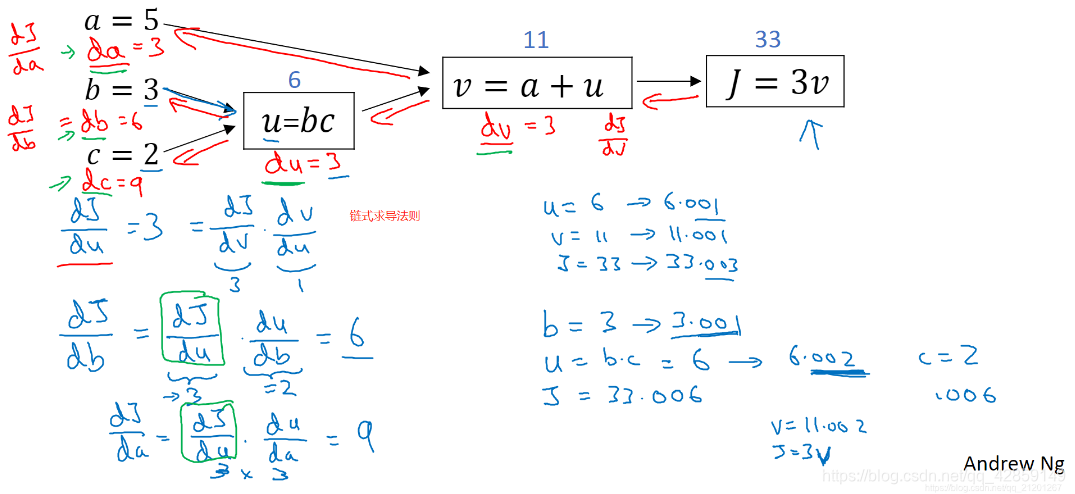
6. 计算图的导数计算
链式求导法则:
7. 逻辑回归中的梯度下降(※)
假设函数和损失函数:
z = w T x + b y ^ = a = σ ( z ) L ( a , y ) = − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) \begin{aligned} &z=w^{T} x+b \\ &\hat{y}=a=\sigma(z) \\ &\mathcal{L}(a, y)=-(y \log (a)+(1-y) \log (1-a)) \end{aligned} z=wTx+by^=a=σ(z)L(a,y)=−(ylog(a)+(1−y)log(1−a))
sigmoid 函数: f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1
sigmoid 求导:
f ( z ) ′ = ∂ f ( z ) ∂ z = − 1 ∗ − 1 ∗ e − z ( 1 + e − z ) 2 = e − z ( 1 + e − z ) 2 = 1 + e − z − 1 ( 1 + e − z ) 2 = 1 1 + e − z − 1 ( 1 + e − z ) 2 = 1 1 + e − z ( 1 − 1 1 + e − z ) = f ( z ) ( 1 − f ( z ) ) \begin{aligned} f(z)^{'}=\frac{\partial f(z)}{\partial z} &=\frac{-1 *-1 * e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1+e^{-z}-1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{1+e^{-z}}-\frac{1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{1+e^{-z}}\left(1-\frac{1}{1+e^{-z}}\right) \\ &=f(z)(1-f(z)) \end{aligned} f(z)′=∂z∂f(z)=(1+e−z)2−1∗−1∗e−z=(1+e−z)2e−z=(1+e−z)21+e−z−1=1+e−z1−(1+e−z)21=1+e−z1(1−1+e−z1)=f(z)(1−f(z))
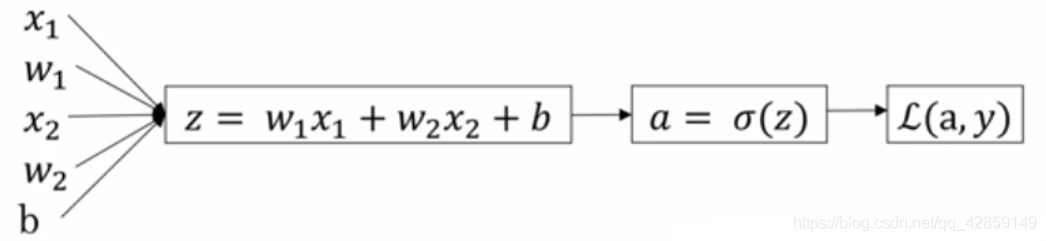
求导过程:
∂ L ∂ a = − y a + 1 − y 1 − a named " d a " ∂ L ∂ z = ∂ L ∂ a ∂ a ∂ z = ( − y a + 1 − y 1 − a ) ∗ a ( 1 − a ) = a − y named " d z " ∂ L ∂ w 1 = ∂ L ∂ z ∂ z ∂ w 1 = x 1 ( a − y ) named " d w 1 " ∂ L ∂ w 2 = ∂ L ∂ z ∂ z ∂ w 2 = x 2 ( a − y ) named " d w 2 " ∂ L ∂ b = ∂ L ∂ z ∂ z ∂ b = a − y named " d b " \begin{aligned} \frac{\partial \mathcal{L}}{\partial a} &=-\frac{y}{a}+\frac{1-y}{1-a} \quad \text { named } \quad "da"\\ \frac{\partial \mathcal{L}}{\partial z} &=\frac{\partial \mathcal{L}}{\partial a} \frac{\partial a}{\partial z}=\left(-\frac{y}{a}+\frac{1-y}{1-a}\right) * a(1-a)=a-y \quad \text { named } \quad "dz"\\ \frac{\partial \mathcal{L}}{\partial w_{1}} &=\frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial w_{1}}=x_{1}(a-y) \quad \text { named } \quad "dw_{1}" \\ \frac{\partial \mathcal{L}}{\partial w_{2}} &=\frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial w_{2}}=x_{2}(a-y) \quad \text { named } \quad "dw_{2}" \\ \frac{\partial \mathcal{L}}{\partial b} &=\frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial b}=a-y \quad \text { named } \quad "db" \end{aligned} ∂a∂L∂z∂L∂w1∂L∂w2∂L∂b∂L=−ay+1−a1−y named "da"=∂a∂L∂z∂a=(−ay+1−a1−y)∗a(1−a)=a−y named "dz"=∂z∂L∂w1∂z=x1(a−y) named "dw1"=∂z∂L∂w2∂z=x2(a−y) named "dw2"=∂z∂L∂b∂z=a−y named "db"
迭代更新:
w 1 : = w 1 − α ∗ d w 1 w 2 : = w 2 − α ∗ d w 2 b : = b − α ∗ d b \begin{aligned} w_{1}:&=w_{1}-\alpha * d w_{1} \\ w_{2}:&=w_{2}-\alpha * d w_{2} \\ b:&=b-\alpha * db \end{aligned} w1:w2:b:=w1−α∗dw1=w2−α∗dw2=b−α∗db
8. m个样本的梯度下降
假设有m个样本,每个样本有2个特征
// 伪代码 from http://www.ai-start.com/dl2017/html/lesson1-week2.html
J=0; dw1=0; dw2=0; db=0;
for i = 1 to mz(i) = wx(i)+b;a(i) = sigmoid(z(i));J += -[y(i)log(a(i))+(1-y(i))log(1-a(i))];dz(i) = a(i)-y(i);dw1 += x1(i)dz(i); // 全部样本的梯度累加dw2 += x2(i)dz(i);db += dz(i);// 求平均值
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;// 更新参数 w, b
w = w - alpha*dw
b = b - alpha*db
显式的使用 for 循环是很低效的,要使用向量化技术加速计算速度。
9. 向量化
使用 numpy 等库实现向量化计算,效率更高
import numpy as np #导入numpy库
a = np.array([1,2,3,4]) #创建一个数据a
print(a)
# [1 2 3 4]
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(c)
print('Vectorized version:' + str(1000*(toc-tic)) +'ms') #打印一下向量化的版本的时间#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):c += a[i]*b[i]
toc = time.time()
print(c)
print('For loop:' + str(1000*(toc-tic)) + 'ms')#打印for循环的版本的时间
上面例子,向量化计算快了600多倍
250241.79388712568
Vectorized version:0.9975433349609375ms
250241.7938871326
For loop:687.734842300415ms
10. 向量化的更多例子
J=0; db=0;
dw = np.zeros((nx,1)) // numpy向量化
for i = 1 to mz(i) = wx(i)+b;a(i) = sigmoid(z(i));J += -[y(i)log(a(i))+(1-y(i))log(1-a(i))];dz(i) = a(i)-y(i);dw += x(i)dz(i); // 向量化,全部样本的梯度累加db += dz(i);// 求平均值
J /= m;
dw /= m;// 向量化
db /= m;// 更新参数 w, b
w = w - alpha*dw
b = b - alpha*db这样就把内层的 d w 1 , . . . d w n dw_1,... dw_n dw1,...dwn 的计算使用向量化了,只用1层 for 循环,还可以做的更好,往下看。
11. 向量化 logistic 回归
逻辑回归前向传播步骤:
- 对每个样本进行计算
z ( 1 ) = w T x ( 1 ) + b z^{(1)}=w^{T} x^{(1)}+b z(1)=wTx(1)+b - 计算激活函数,得到预测值 y ^ \hat{y} y^
a ( 1 ) = σ ( z ( 1 ) ) a^{(1)} = \sigma(z^{(1)}) a(1)=σ(z(1))

可以使用 numpy 来计算:
- Z = n p . d o t ( w T , X ) + b Z = np.dot(w^T, X)+b Z=np.dot(wT,X)+b,+ b 会对每个元素操作,是 numpy 的广播机制。
- A = [ a ( 1 ) a ( 2 ) … a ( m ) ] = σ ( Z ) A=\left[a^{(1)} a^{(2)} \ldots a^{(m)}\right]=\sigma(Z) A=[a(1)a(2)…a(m)]=σ(Z)
这样就没有显式使用 for 循环,计算非常高效。
12. 向量化 logistic 回归梯度输出
Z = w T X + b = n p ⋅ dot ( w . T , X ) + b A = σ ( Z ) d Z = A − Y d w = 1 m ∗ X ∗ d Z T d b = 1 m ∗ n p . sum ( d Z ) w : = w − a ∗ d w b : = b − a ∗ d b \begin{aligned} Z&=w^{T} X+b=n p \cdot \operatorname{dot}(w . T, X)+b \\ A&=\sigma(Z) \\ d Z&=A-Y \\ d w&=\frac{1}{m} * X * d Z^{T} \\ d b&=\frac{1}{m} * n p . \operatorname{sum}(d Z) \\ w:&=w-a * d w \\ b:&=b-a * d b \\ \end{aligned} ZAdZdwdbw:b:=wTX+b=np⋅dot(w.T,X)+b=σ(Z)=A−Y=m1∗X∗dZT=m1∗np.sum(dZ)=w−a∗dw=b−a∗db
非向量化、向量化对比:

这样就向量化的计算,完成了逻辑回归的 1 次迭代,要完成 n_iter 次迭代就在外层加一层 for 循环,这个 for 是省不了的。
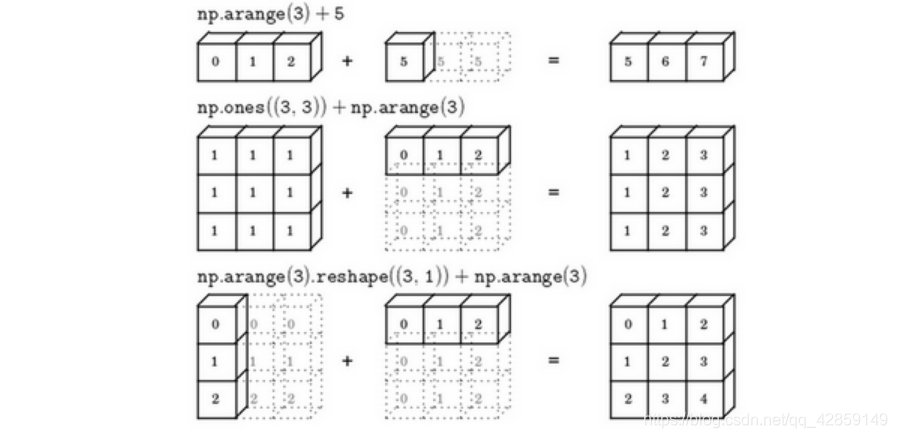
13. numpy 广播机制
import numpy as npA = np.array([[56, 0, 4.4, 68],[1.2, 104, 52, 8],[1.8, 135, 99, 0.9]
])cal = A.sum(axis=0) # 按列求和
print(cal)percentage = 100 * A / cal.reshape(1, 4)
print(percentage)
[ 59. 239. 155.4 76.9]
[[94.91525424 0. 2.83140283 88.42652796][ 2.03389831 43.51464435 33.46203346 10.40312094][ 3.05084746 56.48535565 63.70656371 1.17035111]]
注:axis指明运算 沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行。
- 例1
A = np.array([[1, 2, 3, 4]])
b = 100
print(A+b)

[[101 102 103 104]]
- 例2
A = np.array([[1, 2, 3],[4, 5, 6]])
B = np.array([100, 200, 300])
print(A+B)

[[101 202 303][104 205 306]]
- 例3
A = np.array([[1, 2, 3],[4, 5, 6]])
B = np.array([[100], [200]])
print(A + B)

[[101 102 103][204 205 206]]
- 广播机制与执行的运算种类无关
14. 关于 python / numpy 向量的说明

- 总是使用 nx1 维矩阵(列向量),或者 1xn 维矩阵(行向量);
- 为了确保所需要的维数时,不要羞于 reshape 操作。
这篇关于第一门课:神经网络和深度学习(第二周)——神经网络的编程基础的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





