上干货！小红书“薯条”业务竞价策略及最优公式详解

本文主要是介绍上干货！小红书“薯条”业务竞价策略及最优公式详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

薯条广告业务作为小红书商业化中重要的一部分，可以让内容创作者和企业商家轻松使用手机 app 进行笔记推广和广告投放。虽然从用户视角来看，薯条广告的投放方式简单便捷，但从平台视角来看却面临着很多挑战。如何在薯条广告和其他广告的竞争过程中，合理分配小红书的商业化流量，最大化广告主和平台的整体收益，需要深入地思考和探索。对此，小红书商业技术团队从策略视角出发，对薯条竞价广告的投放进行建模，推导出理论最优解法，再结合业务实践，思考出简单有效的调控方案，让薯条广告业务快速达到了预期水准，推动了商业化平台的发展。

在小红书商业化矩阵中，薯条广告业务是重要一环。具体的业务形式如下图，一个用户（普通用户，KOL，甚至商家）可以通过薯条来推广自己的笔记，过程中只需要简单决定几个选项，如预期曝光量、投放时间、推广目标、人群，付款后就会自动推广了。因为薯条广告的投放过程是需要和商业化流量中其他广告进行竞争的，所以也会完整的涉及竞价广告的三个基本范式，召回、预估、拍卖（竞价）。从业务逻辑上来讲，召回、预估比较贴近业界主流的实践方式，而拍卖（竞价）过程受限于业务复杂性却存在非常多的挑战。

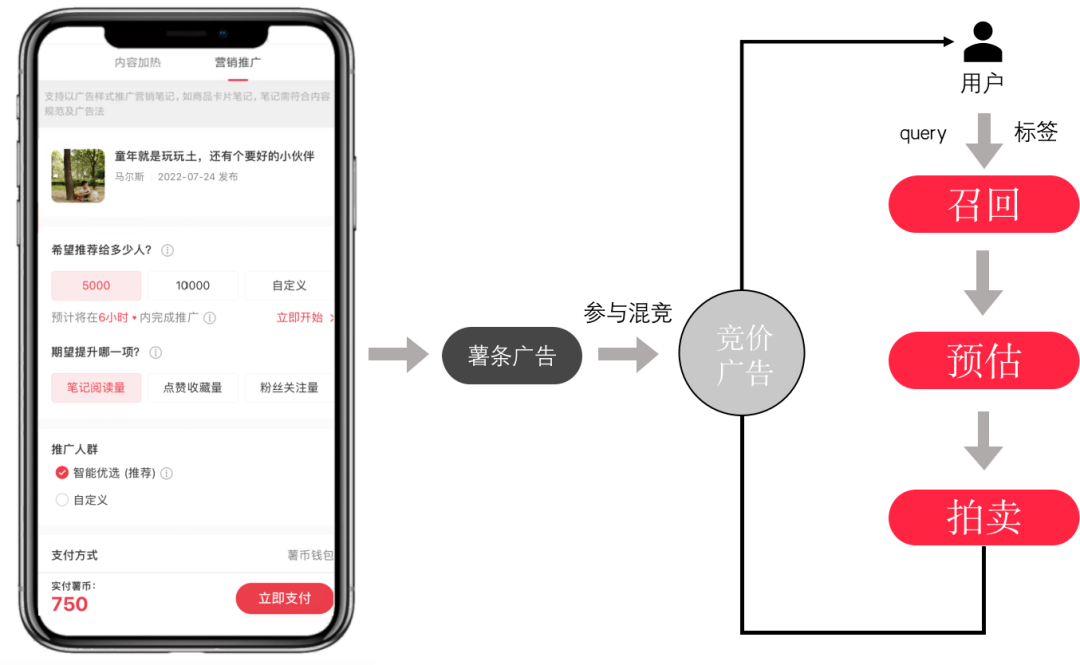
从客户（薯条推广者）的视角来看，薯条是一个比较傻瓜的推广方式，表达了目标、需求曝光量（投放时间）、人群，付款后就开始投放了。但事实上这里存在着诸多隐含的要求：

这个投放是不是平滑的（投放时间内曝光比较均匀的分布）？
最终投放的结果目标转化量如何（比如5k曝光后有多少阅读量）？
最极端的，能不能保量（会不会出现小于预期曝光量的情况）？

当任意一个隐含要求出现问题（发生波动或者和认知发生较大差异时）便会引发客户的反弹（问询或投诉），造成较大的运营压力以及客户使用体感的问题。

从平台的视角来看，薯条是一个保量的业务，在客户付钱的那一刻便签订了一个合约，平台将代客户完成后续的投放。这个过程中有两个核心问题：

如果缺量平台该如何处理？
薯条广告投放过程中会不会出现亏本的情况？

这里平台的亏本可以理解成，每一个薯条订单都会有一个投放的 agent 在小红书的竞价系统中进行自动投放，当然展示薯条的广告就会相应减少其他广告的投放，也即会减少“本应该有的平台收入”；当减少的收入总和大于薯条订单的收入时，平台就出现了亏损，而亏损对于平台的发展而言也是非常严重的问题。

所以，在召回和预估都能正常工作的前提下，如何能从策略视角很好地满足客户与平台的诉求是有很大挑战的。我们从问题的建模出发，对该问题给出了理论的最优解法，再结合实践以及诸多业务考虑，给出了实践中简单有效的调控策略，让薯条业务快速地发展起来，同时也给技术后续的优化留出了足够的空间。

当下小红书主流的流量售卖机制是实时竞价，对于每次广告展示机会都会进行竞价拍卖，将流量分配给效用（utility）最大的广告主并收取一定的费用。在实时竞价过程中，如下图示例，每个薯条的订单作为一个独立的竞价者，由平台的智能 agent 接管竞价，在与其他参竞者竞争过程中还需同时兼顾客户和平台的诸多诉求。

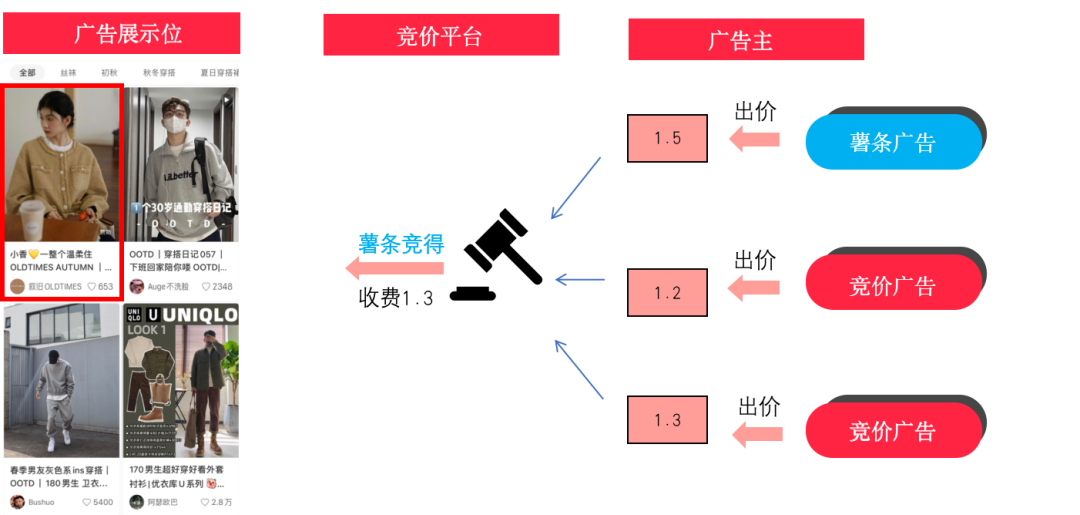
接下来进行薯条竞价投放的建模（注：以下是一种典型业务诉求的建模，真实应用场景会有不同），我们设目标投放量为 D，订单收入为 B，薯条收入的流量 CPM 成本为 M（B/D），投放后的平均转化成本约束为 C（比如优化赞藏订单的赞藏成本）。定向覆盖的流量集合为 $\{pv_i,i=1,\dots, n\}$ ，第 i 个参竞流量的价值设为 $v_i$ （比如优化赞藏，则价值定义为 $pctr_i\times pcvr_i$ ，其中 $pcvr_i$ 代表点击赞藏率）、竞价成本设为 $c_i$ ；用 $x_i \in [0,1]$ 表示是否将该流量分配给当前薯条订单，即竞得时 $x_i=1$ ，未竞得时 $x_i=0$ 。则薯条的业务目标可以形式化为：

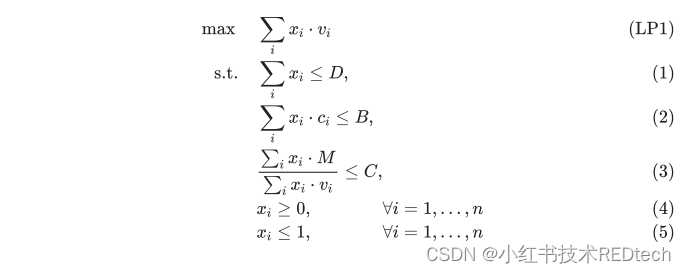
对该问题进行求解，可以得到最优的出价公式如下：

$\begin{aligned} bid^* = \frac{1}{\beta^*}(v_i + \gamma^* \cdot C(v_i-\frac{M}{C})-\alpha^*) \end{aligned}$

其中 $\alpha^*,\beta^*,\gamma^*$ 是需要求解的最优参数，也即当最优参数确定后，按照最优的 $bid^*$ 对每个 pv 进行报价，即可得到 (LP1) 对等的最优解（满足上述若干约束下的目标价值量最大化）。

如果感兴趣可以看下面的最优公式推导过程，也可以直接略过看策略部分的公式解读&实战优化。

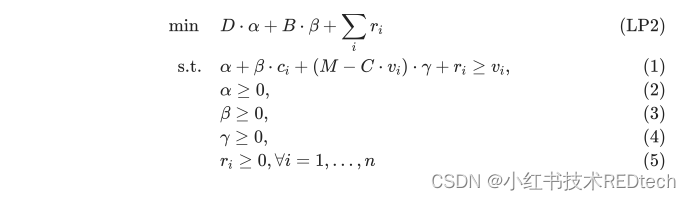
上述线性问题，用其对偶问题表示为，设未知数 $\alpha,\beta,\gamma$ 和 $r_i, \forall i=1,2,\dots,n$ ：

设原问题最优解为 $\{x*| i=1,.., n\}$ ，对偶问题最优解为 $\alpha^*, \beta^*, \gamma^*,\{r_i^*|i=1,\dots,n\}$ ，根据互补松弛定理可得：

$x_i^* \cdot ( v_i - \alpha^*-\beta^* \cdot c_i - (M-C \cdot v_i )\cdot \gamma^* - r_i^* )=0$

$(x_i^*-1)\cdot r_i^*=0, \forall i=1,\dots,n$

此处我们记 $bid_i^*$ 为计划对 $pv_i$ 的最优出价，在 RTB 下（这里假定 second-price auction），薯条和竞价广告混竞，竞得的必要条件是出价不低于该流量的竞价成本，则：

1. 若竞得该pv，即 $x_i^*=1$ ，可推出

$bid^*_i \ge c_i= \frac{1}{\beta}(v_i + \gamma \cdot C(v_i-\frac{M}{C})-\alpha-r_i)$

2. 若未竞得该pv，即 $x_i^*=0$ ，可推出

$r^*_i=0,bid^*_i \leq c_i= \frac{1}{\beta}(v_i + \gamma \cdot C(v_i-\frac{M}{C})-\alpha-r_i)$

在实时广告竞价中，出价与流量价值的比较决定了竞得结果，因此在最优解下，最优出价公式为：

$\begin{aligned} bid^* = \frac{1}{\beta^*}(v_i + \gamma^* \cdot C(v_i-\frac{M}{C})-\alpha^*) \end{aligned}$

假设每天的流量集合已知，则薯条的最优出价参数 $\alpha^*,\beta^*,\gamma^*$ 可以在流量集合已知的前提下求解得到，但实际应用过程中线上流量是未知且波动的，在线应用的方式是根据实时的投放情况对当下使用的参数进行反馈调控，尽可能逼近潜在的最优。

为方便分析，我们令

$a^*=\frac{1}{\beta^*}(1+\gamma^* \cdot C),b^*=\frac{1}{\beta^*}(\gamma^* \cdot M+\alpha^*)$

(1)

则原最优出价公式可以转变为：

$\begin{aligned} bid^* &= \frac{1}{\beta^*}(v_i + \gamma^* \cdot C(v_i-\frac{M}{C})-\alpha^*) \\ &=a^*v_i-b^* \end{aligned}$

这样，我们将三参数调控问题，化简成双参调控。我们将某个薯条订单可参竞的流量按照价值 $v_i$ 和成本 $c_i$ 画出分布图（每一个点代表一个可竞得的流量），那么出价公式是该分布下的线性函数（自变量是 $v_i$ ，因变量是 $bid_i$ ），通过调控函数的斜率 a 和截距 b，对当前的流量进行划分，函数之下的流量均可竞得，函数之上的流量不竞得。通过对 a, b 的上调或下调，可以控制竞得流量的集合，最优公式下方的所有流量即为原问题最优的竞得流量集合。如下图所示。

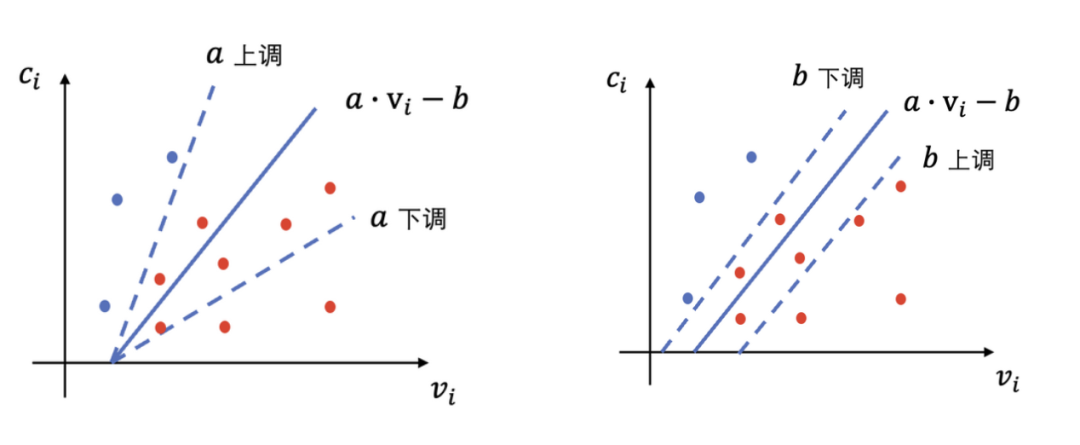
然而，从最优公式推导可以知道， $\alpha,\beta,\gamma$ 三个参数分别对应着展现量、利润率和转化成本约束，化简为双参数调控后，由公式（1）可知，每次 a 和 b 的调控都会同时影响多个约束。所以对于调控策略而言，需要有一个面向终极目标调控 $\alpha,\beta,\gamma$ 三个参数（也即 a 和 b）的 policy，也即能够很好地平衡参数调整后对于不同约束的影响。这里面的难点可以用下面的例子说明：

如果当前的流量获取速度低于预期需要提升出价，降低 $\alpha$ 、降低 $\beta$ 、提升 $\gamma$ 都可以做到，就会有非常多种组合来达到提升拿量的预期，但不同的组合又会对利润率、转化成本造成侧面的影响；所以简单的单目标调控（一般的 PID 锚定单一目标进行控制）会让最终结果距离最优结果有很大空间。

参考业内的一些方法 [1] ，可以使用强化学习来建模，端到端的学习最优的调控策略（policy）来优化投放结果，但方法本身比较难在短时间内落成（训练环境、在线推理）。所以我们这里对问题进行进一步分析，希望能得到一种简单有效的调控方案，快速达到业务预期。

当前形式化的投放场景有两个明显的先验知识：

竞价过程中，出价过高会导致利润率风险，而薯条场景下有非常好的一个出价上限标的，即流量成本 M（M=B/D）。考虑到二价率，设置按照 M 做一定上浮作为每个 pv 的出价上限是个不错的实践，可以很好的规避竞得成本过高的流量（实际应用中预估 $v_i$ 过高也会导致过高的出价）。
因为薯条是保量逻辑（竞得流量和需求基本对等），所以竞得的流量平均转化率 $\overline{v}$ 是有个下限的，过低会导致最终的转化成本过高（参考 LP1 的第三个约束）。所以在竞价过程中过滤掉转化率 $v_i$ 过低的流量是个很好的实践，能够进一步简化竞价的难度。

所以，我们如果考虑以 v=M/C（也即临界流量价值）和出价函数的交点 R 为中心，将流量集合划分为四个区域，分别对应成本和价值叉乘的四部分。不难想到我们不希望竞得成本高但价值低的流量以及成本低价值低的流量。所以作为一个简单有效的实践，可以对流量集合进行初步的过滤（v 小于 M/C 的过滤掉，并且成本高于 B/D 的过滤掉），此时我们的原问题就变得很简单了。

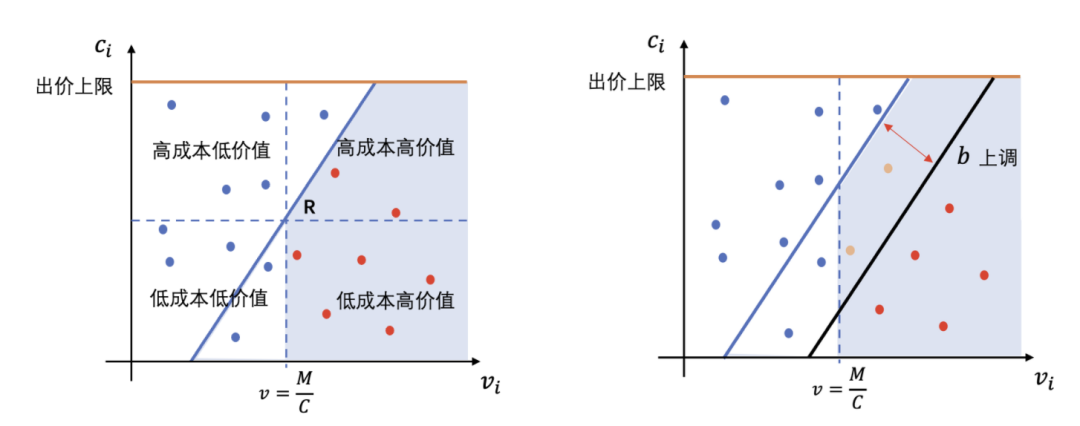
在这样的设置下，公式（1）的 a 和 b 的选择容错性会更好，直观的理解就是硬性地规避了上图蓝色流量。同时，通过我们离线的观测，公式（1）中的 a 天与天之间的变化并不显著，所以我们为了进一步简化调控，将 a 设置成历史上的最优 a（固定住），然后通过调整 b 来控制一天的拿量速率（见上图右图），这样简单的 PID 策略（比例误差定义为单位时间内的竞得流量与期望流量的 diff，期望流量通常使用大盘流量潮汐的 pattern 计算）即可让我们逼近最优解。