本文主要是介绍永磁无感博士论文阅读(杨子辉2012),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
主要观点
-
脉冲电压法辨识转子初始位置
预定位法的局限性:
T 0 = 3 2 ψ p m I s sin θ lim 因此: θ lim = sin − 1 2 T 0 3 ψ p m I s T_0=\frac{3}{2}\psi _{pm}I_s\sin \theta _{\lim} \\ \text{因此:}\theta _{\lim}=\sin ^{-1}\frac{2T_0}{3\psi _{pm}I_s} T0=23ψpmIssinθlim因此:θlim=sin−13ψpmIs2T0
受负载摩擦转矩、输出电流大小确定。而且可能导致相位角度在180度附近。优化的方法时进行二次定位。

初始位置辨识法: 根据电机的凸极饱和效应计算转子的初始位置,定位精度高,而且不会使转子随机转动。理论依据使电感检测测量法。见理论推导部分。辨识初始位置时,不同电压矢量导致的不同的饱和效用如下图所示。需要注意的是虽然q轴电感大于d轴电感,但是在注入不同方向的电流矢量时,由于饱和效应,d轴正向注入时实际的Ld将小于静态Ld。

改进的5脉冲法辨识了转子位置和NS极。有较好的使用价值。 也可以采用7脉冲法进行辨识。
-
IF启动电流闭环,转矩攻角自平衡问题
传统的VF模式,由于定子阻抗压降由定子电压和反电势决定,对于永磁同步电机,反电势和转速有关,因此若定子电压较大,则容易产生过流问题。

采用IF模式后,电流的反馈至受期望值约束当反电势变化时,电流自然受控,不会出现过流问题。但如何避免失步问题?
攻角定义:?是否时转子位置与电流矢量的夹角?
一般情况下,IF模式运行时通常保证攻角不大于45度。由于不同转速下的负载大小不同,常需设置转速和电流的流频比曲线。常见的负载如:风机水泵负载、恒转矩负载、恒功率发u在、一次负载、二次负载(大多数风机水泵)、不规则负载。;这里的几次指的是: I = C ∗ f 2 I=C*f^2 I=C∗f2。若负载为不规则负载,则需要根据最大转矩电流,才能保证稳定运行。通常的电流模式如下公式: I s = I 0 / sin 4 5 ° + C 0 I_s=I_0/\sin 45^{\degree}+C_0 Is=I0/sin45°+C0
永磁同步电机的常用控制方法: I d = 0 , c o s p h i = 1 I_d=0,cosphi=1 Id=0,cosphi=1,恒磁通控制、最大转矩电流比控制、弱磁控制、最大输出功率控制等;最优定子电流控制。 -
电流开闭环切换方案
重点在于速度转矩的平滑过渡; IF切换方法:逐渐以一定的斜率减小q轴电流,使攻角自然变化至90度所在位置。当转矩电流矢量与iq相近时,进行切入。此时d轴误差近似为0,这是在隐极电机中成立的方案。缺点无法进行0s加速; -
反电势积分法
磁链估计模型:

基本思路:采样电机定子的瞬时值电压和电流,计算电子定子磁链、转子磁链和反电势矢量。从而得到转子位置信息,在进一步得到转速信息。对于标贴式电机是很容易计算的。
当位置角估计不准时,会造成坐标变换的角度不准,从而使q轴转矩电流比理想值偏大,系统可以稳定运行,但是影响运行效率。 估计速度的稳定性会影响速度环PI环的调节能力,不稳定的估算速度在系统动态调整时容易引发震荡。
当电阻估值值偏大师时,导致磁链位置估计偏大。

当电感估计值偏大时,导致角度估计偏小;当电流测量偏大时,角度误差估计偏小;当电压估计篇大时,角度误差估计偏大;虽然由于d轴固有磁通导致d轴容易进入饱和,但是由于id=0控制下,电流集中在q轴,因此q轴的饱和更显著。(参考文献107);特别是在重载情况下,较大的转矩电流不仅使q轴电感减小,同时也会影响d轴电感。

-
电流测量偏差对算法的影响
电流偏差可表示为: Δ i = i ^ − i = e g a i n sin ω t + e o f f \varDelta i=\widehat{i}-i=e_{gain}\sin \omega t+e_{off} Δi=i −i=egainsinωt+eoff,其中 e g a i n , e o f f e_gain,e_off egain,eoff分别表示增益偏差和直流偏置误差,该误差在dq坐标系下将导致直流分类、1倍频和2倍频。(参考文献114);
主要理论推导和公式
- 表贴式电机: [ u α u β ] = [ R s 0 0 R s ] [ i α i β ] + d d t [ ψ α ψ β ] { ψ α = L 1 i α + ψ p m cos θ r ψ β = L 1 i β + ψ p m sin θ r θ r = tan − 1 ψ β − L 1 i β ψ α − L 1 i α \text{表贴式电机:} \\ \left[ \begin{array}{c} u_{\alpha}\\ u_{\beta}\\ \end{array} \right] =\left[ \begin{matrix} R_s& 0\\ 0& R_s\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ \end{array} \right] +\frac{d}{dt}\left[ \begin{array}{c} \psi _{\alpha}\\ \psi _{\beta}\\ \end{array} \right] \\ \begin{cases} \psi _{\alpha}=L_1i_{\alpha}+\psi _{pm}\cos \theta _r\\ \psi _{\beta}=L_1i_{\beta}+\psi _{pm}\sin \theta _r\\ \end{cases} \\ \theta _r=\tan ^{-1}\frac{\psi _{\beta}-L_1i_{\beta}}{\psi _{\alpha}-L_1i_{\alpha}} 表贴式电机:[uαuβ]=[Rs00Rs][iαiβ]+dtd[ψαψβ]{ψα=L1iα+ψpmcosθrψβ=L1iβ+ψpmsinθrθr=tan−1ψα−L1iαψβ−L1iβ
上述方法在10%的额定转速以上具有良好的转速和位置跟踪效果。但低于5%转速以下时,估计结果不稳定。另外在低速区需要将死区补充做好才可以进一步提高精度。
转子初始位置辨识方法:
[ u α 1 u α 2 u β 1 u β 2 ] = R s [ i α 1 i α 2 i β 1 i β 2 ] + [ L 1 + L 2 cos 2 θ r L 2 sin 2 θ r L 2 sin 2 θ r L 1 + L 2 cos 2 θ r ] ∗ [ d d t i α 1 d d t i α 2 d d t i β 1 d d t i β 2 ] [ L 1 + L 2 cos 2 θ r L 2 sin 2 θ r L 2 sin 2 θ r L 1 + L 2 cos 2 θ r ] = [ u α 1 − R s i α 1 u α 2 − R s i α 2 u β 1 − R s i β 1 u β 2 − R s i β 2 ] [ d d t i α 1 d d t i α 2 d d t i β 1 d d t i β 2 ] − 1 \left[ \begin{matrix} u_{\alpha 1}& u_{\alpha 2}\\ u_{\beta 1}& u_{\beta 2}\\ \end{matrix} \right] =R_s\left[ \begin{matrix} i_{\alpha 1}& i_{\alpha 2}\\ i_{\beta 1}& i_{\beta 2}\\ \end{matrix} \right] +\left[ \begin{matrix} L_1+L_2\cos 2\theta _r& L_2\sin 2\theta _r\\ L_2\sin 2\theta _r& L_1+L_2\cos 2\theta _r\\ \end{matrix} \right] *\left[ \begin{matrix} \frac{d}{dt}i_{\alpha 1}& \frac{d}{dt}i_{\alpha 2}\\ \frac{d}{dt}i_{\beta 1}& \frac{d}{dt}i_{\beta 2}\\ \end{matrix} \right] \\ \left[ \begin{matrix} L_1+L_2\cos 2\theta _r& L_2\sin 2\theta _r\\ L_2\sin 2\theta _r& L_1+L_2\cos 2\theta _r\\ \end{matrix} \right] =\left[ \begin{matrix} u_{\alpha 1}-R_si_{\alpha 1}& u_{\alpha 2}-R_si_{\alpha 2}\\ u_{\beta 1}-R_si_{\beta 1}& u_{\beta 2}-R_si_{\beta 2}\\ \end{matrix} \right] \left[ \begin{matrix} \frac{d}{dt}i_{\alpha 1}& \frac{d}{dt}i_{\alpha 2}\\ \frac{d}{dt}i_{\beta 1}& \frac{d}{dt}i_{\beta 2}\\ \end{matrix} \right] ^{-1} [uα1uβ1uα2uβ2]=Rs[iα1iβ1iα2iβ2]+[L1+L2cos2θrL2sin2θrL2sin2θrL1+L2cos2θr]∗[dtdiα1dtdiβ1dtdiα2dtdiβ2][L1+L2cos2θrL2sin2θrL2sin2θrL1+L2cos2θr]=[uα1−Rsiα1uβ1−Rsiβ1uα2−Rsiα2uβ2−Rsiβ2][dtdiα1dtdiβ1dtdiα2dtdiβ2]−1
再根据电感矩阵即可计算出转子位置角。上述辨识只能辨识转子位置,无法辨识NS极,因此还需要进一步施加电压矢量来区分NS极。通过d轴正向和反向的电压激励,从而得到不同的电流响应,沿d轴方向的电压矢量对d轴实现了充磁效应导致d轴饱和,从而电流幅值增大,另一个电压矢量对d轴起去磁作用,从而导致电流响应的幅值减小。对比两次电流幅值,即可判断得到的位置是在N极还是s极。
理论依据是RL电路的零状态响应。
{ U = R i + L d i ( t ) d t i ( 0 ) = 0 \begin{cases} U=Ri+L\frac{di\left( t \right)}{dt}\\ i\left( 0 \right) =0\\ \end{cases} {U=Ri+Ldtdi(t)i(0)=0
上式还可以进行电感辨识。
有效磁链的概念:
u → α β = R s i → α β + d ψ → α β d t ψ → α β = ( ψ p m + L d i d + j L q i q ) e j θ r ψ → α β = ( ψ p m + L d i d + j L q i q + L q i d − L q i d ) e j θ r ψ → α β = ( ψ p m + L d i d − L q i d ) e j θ r + ( j L q i q + L q i d ) e j θ r ψ → α β = ( ψ p m + ( L d − L q ) i d ) e j θ r + L q i → α β \overrightarrow{u}_{\alpha \beta}=R_s\overrightarrow{i}_{\alpha \beta}+\frac{d\overrightarrow{\psi }_{\alpha \beta}}{dt} \\ \overrightarrow{\psi }_{\alpha \beta}=\left( \psi _{pm}+L_di_d+jL_qi_q \right) e^{j\theta _r} \\ \overrightarrow{\psi }_{\alpha \beta}=\left( \psi _{pm}+L_di_d+jL_qi_q+L_qi_d-L_qi_d \right) e^{j\theta _r} \\ \overrightarrow{\psi }_{\alpha \beta}=\left( \psi _{pm}+L_di_d-L_qi_d \right) e^{j\theta _r}+\left( jL_qi_q+L_qi_d \right) e^{j\theta _r} \\ \overrightarrow{\psi }_{\alpha \beta}=\left( \psi _{pm}+\left( L_d-L_q \right) i_d \right) e^{j\theta _r}+L_q\overrightarrow{i}_{\alpha \beta} uαβ=Rsiαβ+dtdψαβψαβ=(ψpm+Ldid+jLqiq)ejθrψαβ=(ψpm+Ldid+jLqiq+Lqid−Lqid)ejθrψαβ=(ψpm+Ldid−Lqid)ejθr+(jLqiq+Lqid)ejθrψαβ=(ψpm+(Ld−Lq)id)ejθr+Lqiαβ
查漏补缺
- 再次复习 α β \alpha\beta αβ坐标系下的磁链方程。
- 参考文献60~63.
- 参考文献91.
- 63页的公式是否存在问题?
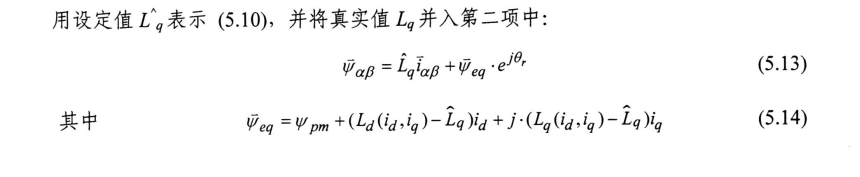
- 当q轴电感饱和情况下引起的定向偏差分析?
阅读效率
已完成阅读。
这篇关于永磁无感博士论文阅读(杨子辉2012)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









