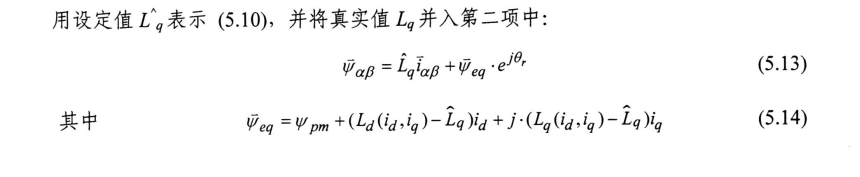博士论文专题
华人首次!清华姚班助理教授张焕晨获得SIGMOD Jim Gray博士论文奖!
来源:AI科技评论本文约1000字,建议阅读5分钟清华姚班助理教授张焕晨获得SIGMOD Jim Gray博士论文奖。 近日,ACM SIGMOD公布了2021年吉姆·格雷博士论文奖(SIGMOD Jim Gray Doctoral Dissertation Award)的最终获奖者,他就是目前正就职于清华大学交叉信息研究院(姚班)的助理教授张焕晨! 该奖项始于2006年,以1998年图灵
【博士论文】视觉语言交互中的视觉推理研究
来源:专知本文为论文,建议阅读5分钟本文通过单轮交互和多轮交互两个场景,分别选取指称语理解和视觉对话两个代表性任务进行阐述。 来自中国人民大学牛玉磊的博士论文,入选2021年度“CCF优秀博士学位论文奖”初评名单! https://www.ccf.org.cn/Focus/2021-11-22/750448.shtml 语言交互中的视觉推理研究 视觉语言是计算机视觉与自然语言处理的交叉领域
【博士论文】机器学习中的标记增强理论与应用研究
来源:专知本文为论文,建议阅读5分钟本文对标记增强进行研究。 来自东南大学徐宁的博士论文,入选2021年度“CCF优秀博士学位论文奖”初评名单! https://www.ccf.org.cn/Focus/2021-11-22/750448.shtml 机器学习中的标记增强理论与应用研究 标记端多义性是当今机器学习的热点问题。多标记学习中,每个样本都被赋予一组 标记子集来表示其多种语义信息。然
【长文阅读】MAMBA作者博士论文<MODELING SEQUENCES WITH STRUCTURED STATE SPACES>-Chapter2
Gu A. Modeling Sequences with Structured State Spaces[D]. Stanford University, 2023. 本文是MAMBA作者的博士毕业论文,为了理清楚MAMBA专门花时间拜读这篇长达330页的博士论文,由于知识水平有限,只能尽自己所能概述记录,并适当补充一些相关数学背景,欢迎探讨与批评指正。内容多,分章节更新以免凌乱。 Chap
腾讯高级研究员博士论文走红,称“计算机终于成了我一生的事业与希望”
“我走了很远的路,吃了很多的苦,才将这份博士学位论文送到你的面前。二十二载求学路,一路风雨泥泞,许多不容易。如梦一场,仿佛昨天一家人才团聚过。” 整理 | 王晓曼 出品 | 程序人生 (ID:coder _life) 4月18日,中科院一博士论文的《致谢》部分内容登上微博热搜,在微博达到了6.3亿次阅读,12.1万次讨论。 作者在《致谢》中讲述了自己为了走出小山坳所付出的努力和艰辛,这种
【苏黎世联邦理工博士论文】深度强化学习的体系结构
来源:专知本文为论文介绍,建议阅读5分钟本文不关注实证结果,而是从研究反向传播在架构设计和训练中的简单数学含义开始。 自从深度学习和深度强化学习出现以来,已经有大量的经验成功地利用某种人工神经网络来解决给定的优化问题。然而,许多公司的内部运作方式只被人们模糊地了解,并隐藏在成功的故事中。通过揭示各种含义,这篇论文试图建立一个理解为什么某些神经网络架构设计工作,以及关键的是为什么其他的不能
只愿年过半百,归来仍是少年-爆火的博士论文致谢,本人回应:祝愿大家努力终有所成!...
杨净 鱼羊 发自 凹非寺量子位 报道 | 公众号 QbitAI “理想不伟大,只愿年过半百,归来仍是少年,希望还有机会重新认识这个世界,不辜负这一生吃过的苦。最后如果还能做出点让别人生活更美好的事,那这辈子就赚了。” 这个周末,一位博士因为自己的博士论文致谢,火爆全网。 不同于以往常见的论文致谢,这篇致谢未以“感谢XXX”的格式开篇,而是以“我走了很远的路,吃了很多的苦,才将这份博士学位论文
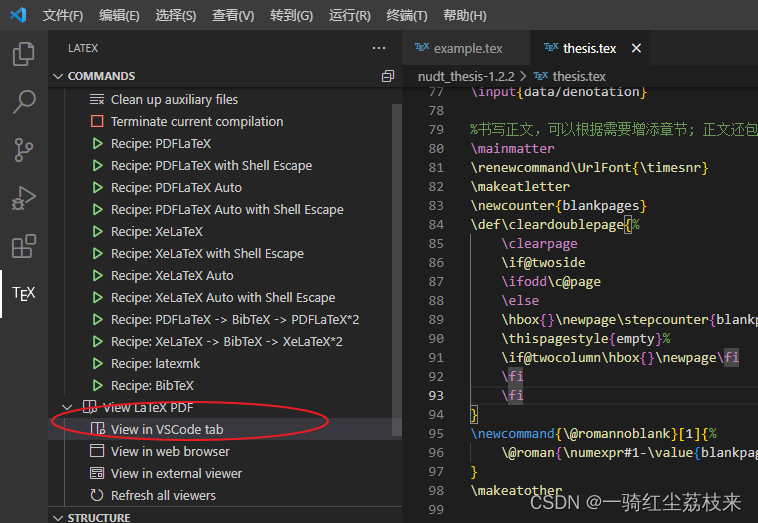
【博士论文latex写作】
1.安装编译器 到官网下载镜像:https://mirrors.hit.edu.cn/CTAN/systems/texlive/Images/ 选择 texlive2023.iso 也可选择百度云2022版本: 链接:https://pan.baidu.com/s/1WLVX8Zn1E4hIYRupLBabNA?pwd=gm63 提取码:gm63 打开后,运行其中的`install-
永磁无感博士论文阅读(杨子辉2012)
主要观点 脉冲电压法辨识转子初始位置 预定位法的局限性: T 0 = 3 2 ψ p m I s sin θ lim 因此: θ lim = sin − 1 2 T 0 3 ψ p m I s T_0=\frac{3}{2}\psi _{pm}I_s\sin \theta _{\lim} \\ \text{因此:}\theta _{\lim}=\sin ^{-1}\frac{