论文笔记-When Do GNNs Work: 理解和改进邻域聚合

论文标题：When Do GNNs Work: Understanding and Improving Neighborhood Aggregation (IJCAI-20)
论文链接：www.ijcai.org
论文代码：github

更多图神经网络和深度学习内容请关注：

摘要

图神经网络（GNNs）在大量图相关任务中都表现出强大的性能。虽然GNN模型有很多种，但他们都有一个共同点：邻域聚合，邻域聚合中每个节点的嵌入都是通过邻域（这里指的是扩展的领域，即结点本身也是自身的邻居）的嵌入来更新的。

本文旨在通过提出以下问题来更好地理解这一机制：邻域聚合是否总是有必要的和有益的？ 简而言之，答案是否定的，我们找出两种情况下邻域聚合是没有帮助的：

（1）当节点的邻域（邻居）高度不相似时；
（2）当节点的嵌入已经与其邻域非常相似时。

为此，我们提出了两个新的度量方法（neighborhood entropy和center-neighbor similarity），可以定量地度量这两种情况，并将它们集成到一个自适应的层模块中。

注：论文中的"我们"等第一人称都指的是论文作者

引言

尽管GNN在多个数据集中取得了巨大成功，但我们观察到，在某些情况下，与无法访问图中边信息的简单FNN（fully-connected neural network）相比，改进是有限的，特别是当聚合度（即聚合轮数，指的是GNN层数）较大时，如表1所示。然后论文认为邻域聚合在某些的情况下是有害的或者是不必要的。

现有的研究表明：深层图神经网络将来自不同簇的节点混合在一起，并将这种现象命名为“过度平滑”。然而现有的研究没有从局部角度（local perspective）考虑不同的聚集度(即聚合的次数，同GCN中的层数)。事实上，如果我们允许聚合度在节点之间变化，那么GNN的性能可以得到显著提高（如表1的最后一行所示）。下一个问题是如何控制单个节点的聚合度？

使用不同聚合度在Cora（3%标签）数据集上进行节点分类的性能。对于按结点聚合（Node-wise Agg），我们手动确定所有节点的聚集度。在这个实验中，我们使用GCN，CNN是一个典型的GNN模型。

为了实现这个目标，我们试图描述对聚合没有帮助的情况 。具体地说，对于单个节点，我们分析了基于其自身及其直接邻域的特征/预测标签的邻域聚合的效用。我们发现：

1. 如果中心节点的邻居学习到的特征/标签不一致（具有较高的熵），则进一步的聚合可能会影响性能；
2. 当中心节点的学习到的特征/标签与其邻居几乎相同时，不需要进一步的聚合。

对于每一个场景，我们都设计了一个基于信息论的直观的和有原则的度量来进行量化。

为了充分利用我们的度量标准，充分发挥神经网络的潜力，我们设计了一个自适应层模块，其允许单个节点执行不同次数的邻域聚合。具体来说，在训练过程中，我们检查每个节点及其邻居的学习到的标签，通过计算我们的度量来估计邻域聚合是有害的或者不必要的，并且只允许有用的节点进行聚合。循环执行上述过程，直到执行了规定的最大次数的迭代操作，或者所有节点都不允许执行聚合操作。我们进行了广泛的实验，以验证和解释我们提出的方案的优势。

综上所述，我们的主要贡献是：

1. 从局部角度分析了邻域聚合的效用，并给出了例证、理论支持和实验结果；
2. 提出了两个度量方法（neighborhood entropy和center-neighbor similarity），定量描述了邻域聚合无益的两种情形；
3. 将将该指标引入到一种新颖的自适应层模块的设计中，通过在三个实际网络(数据集)上的大量实验验证了该模块的性能。

基础知识

Graph Neural Networks (GNN)

Simple Graph Convolution (SGC)

SGC[Wuet al.，2019]通过消除层间非线性(指的应该是激活函数)简化了GCN。SGC已被证明具有与GCN相同的性能的同时提高了效率。使用单一线性投影的另一个好处是，SGC中的参数数量不随卷积层数量的增加而增加，从而避免了过拟合现象。SGC模型可以表示为

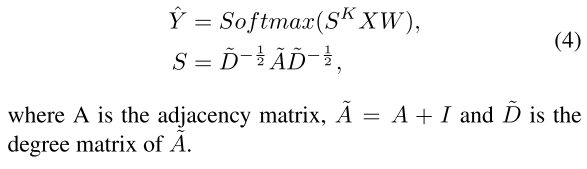
分析

在本节中，我们从一个案例研究开始，探讨在哪些情况下邻域聚合可能对GNNs没有帮助。GNN更新函数由非线性、线性投影和邻域聚合等操作组成。为了避免引入混淆因素（如过度拟合），我们使用SGC[Wuet al.，2019]作为研究的基础模型。

Zachary的空手道俱乐部[Zachary，1977]（图1）是一个包含俱乐部成员之间相互作用的经典数据集。俱乐部成员可分为两组：如黄色和蓝色节点所示。

我们从逐渐增加这个数据集上SGC的聚集度（也就是层数）L，从1、3到5，观察信息如何在聚合过程中传播（如下图，L=1、L=3、L=5对应的分别是子图1、2、3)。

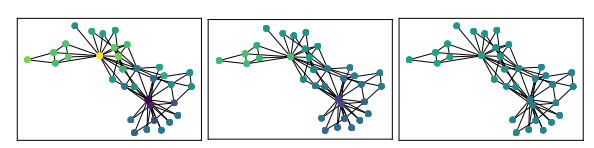
当L=1时，初始标记的节点（子图1中的黄色结点）明显突出，信息只传播给其直接邻居（即一跳邻居），不能在所有俱乐部成员之间充分传播。
当L=3时，同一俱乐部之间的预测非常相似，但俱乐部之间的区别仍然比较明显。
当L继续增加（L=5及以上）时，不同类别结点的区别开始模糊，最后所有节点都有相同的预测。这种现象被Liet称为过度平滑（over-smoothing）。

为了获得最佳分类效果，我们需要邻域聚合，但是必须避免过度聚合。 避免过度聚合的关键是防止inter-club，即是防止社区(社区也称为类别)之间（inter-community）的混合，这个混合在聚合操作跨越社区边界（节点13、19、1、2）时发生。 这些节点的主要特征是其邻居具有不同的标签，为此我们提出了第一个度量-邻居熵（neighborhood entropy）。

此外，最佳聚集度因节点而异：当L = 1时，右组（节点32、33、14、29）已经比较肯定地产生了正确的预测，而顶部的节点（节点0、11、12、17）仍然可靠 需要更多的聚合。 对于这些比较肯定地产生了正确的预测节点，进一步的聚合只会增加计算成本，而不会提高性能。 因此，我们得出了第二个度量中心-邻居相似度（center-neighbor similarity）。

第一行:使用SGC的空手道俱乐部数据表上的预测结点标签。节点的颜色显示预测的俱乐部类别。
第二行:计算节点的邻域熵。颜色越深熵越低。
第三行：计算中心邻居相似性。颜色越深，相似性越小。
从左到右:聚合度（也就是模型层数）L= 1;3;5。
初始已标签结点的数量分别是16(带有标签0)和14(带有标签1)

Neighborhood Entropy

邻域聚合（Neighborhood aggregation）利用了网络中的同质效应（ homophily effect,论文的同质效应和聚类假设应该是同义），即连接的节点应该是相似的。更进一步说，节点的邻居之间应该是相似的。当邻居是不相似的时，我们将此视为警告：同质效应假设可能不成立，聚合信息可能是噪声。

为了衡量一个特定节点的邻居的多样性，我们计算了邻居之间的熵:

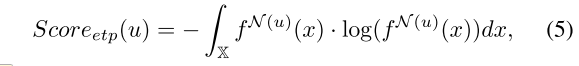
其中$X$是特征空间，$f^{N(u)}$是节点$u$的邻居特征的概率密度函数（PDF）。由于该PDF是高维空间上每个邻居的Dirac函数之和，因此微分熵是不可计算的。

我们使用预测的标签来计算节点$u$的邻居标签分布并计算其离散熵：

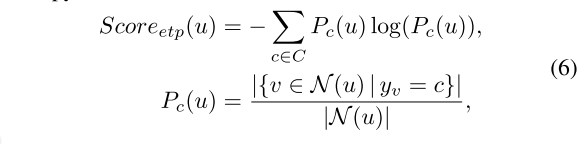
其中$C$是所有标签类的集合。

如果$Scor{e}_{etp}(u)$较大，则节点$u$邻居的多样性比较大(即节点$u$邻居不都是同一个类别的)。 对于图1所示的空手道俱乐部数据集，假设正确预测标签时，$Scor{e}_{etp}(9）=0.673$，比$Scor{e}_{etp}(6)=0$大得多，这表明节点9的邻居比节点6的邻居更加多样化。

Center-Neighbor Similarity

当节点的特征与其邻居足够相似时，邻域聚合可能是冗余的 。例如，当L=1时，图2中节点25的标签已经与其所有邻居相同，因此聚合操作不会更改其标签，因此聚合操作是不必要的。

我们通过计算中心节点与其邻居节点之间的逐点互信息（PMI）来描述这种相似性特点，由于我们没有邻居特征的概率分布的先验知识，因此我们假设它遵循均匀分布，这使得P(N(u))为常数。 然后将相似性定义如下：

其中结点u是中心节点，$N(u)$是$u$的邻居集，$f_u$是$u$的节点特征，该特征可以是节点的输入特征、学习的嵌入或预测的标签。

类似地，我们可以使用one-hot编码预测标签来计算度量

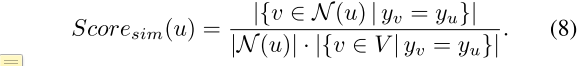
如果$Scor{e}_{sim}(u)$较大，则节点$u$与它的邻居$N(u)$更相似。 在这种情况下，我们可以比较邻域聚合前后的性能，并证明预测结果几乎相同，如以下定理1中正式表述的

Putting Metrics to Test

在上文中，我们描述了我们提出的两个度量指标neighborhood entropy和center-neighbor similarity背后的动机和理论分析。当neighborhood entropy或center-neighbor similarity较高时，我们在执行聚合时应该更加谨慎。

我们将建议的度量标准进行测试，如下图的第二行和第三行所示。第二行显示了计算的邻域熵（neighborhood entropy），而更深的颜色意味着较低的熵。从左到右看，高熵节点逐渐从图的顶部转移到中间，并汇聚在应该扮演不同结点类别“看门人”角色（两种类别结点交界处的结点）的节点上。

第三行显示计算出的中心邻域相似度(center-neighbor similarity)。右下组经过1轮聚合后相似度较高，且在整个聚合过程中保持一致。作为比较，左上方的节点最初与其邻居的相似度较低，这表明需要更多的聚合。乍一看，这两行（第二和第三行）可能看起来完全相反，而且这两个指标确实是为处理频谱两端（两个极端）的情况而设计的。可从进一步聚合中受益的节点不属于这两个类别，并且应该具有较低的neighborhood entropy和center-neighbor similarity值。我们可以看到，随着聚合度的增加，属于此类的节点逐渐消失，表明不需要再进行聚合。

模型

根据前面的分析，我们提出了一个 自适应层模块（Adaptive-layer module），该模块允许节点在每轮邻域聚合中做出单独的决策，因此不同节点可能会有不同的聚合度（即每个结点的聚合次数可能不一样 。

具体来说，在每一层中，我们应用一个门控函数来控制邻域信息的影响。它的值由$Scor{e}_{sim}$和$Scor{e}_{etp}$决定。我们使用类似于SGC的方法去除层之间的所有非线性。我们的模块结构如下：

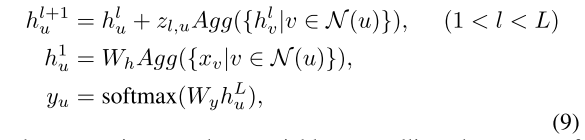
其中$z_{l,u}$是控制邻域聚合使用的随机变量(门)。

我们的更新操作类似于残差层。 此设计有两个考虑因素：

1. 已知残差层可以堆叠更多的层；
2. 能够使用相同投影矩阵$W_y$将隐藏状态$h_u^l$投影到每一层的标签上

门$z_{l,u}$是使用以下公式从$Scor{e}_{sim}$和$Scor{e}_{etp}$计算得出的

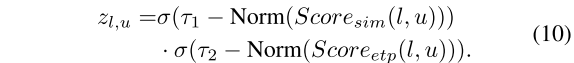
其中激活函数σ将$z$的值压缩为(0,1)

ALaGCN模型。在第一层中，使用矩阵$W_y$将输入特征$X$的维数减少到$h_u^l$的维数。省略了额外的聚合层.

当$Scor{e}_{sim}$和$Scor{e}_{etp}$中的任何一个的值较大时，$z$取接近0的较小值。Norm是一种批量标准化操作，用于重新缩放Score，以便在不同层之间进行比较。

为了简单起见，我们使用one-hot编码的预测标签来计算模型中的$Scor{e}_{sim}$和$Scor{e}_{etp}$。由于我们在实践中没有实际类别大小的先验知识，因此我们假设所有label类别的大小都相同。所以label大小是一个常量，不需要计算。

与基于注意力的模型相比，我们可以扩展基础模型来处理邻居的注意力权重

其中$a_{u,v}^l$是第l层中node u与node v的注意系数，其计算方法与[Velick-Ovick等人，2017]类似。

我们还可以通过为每个注意头计算不同的z来将我们的度量扩展到multi-head attention，表示为$z_{l,u}^k$