本文主要是介绍格林公式中对偏微分的积分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
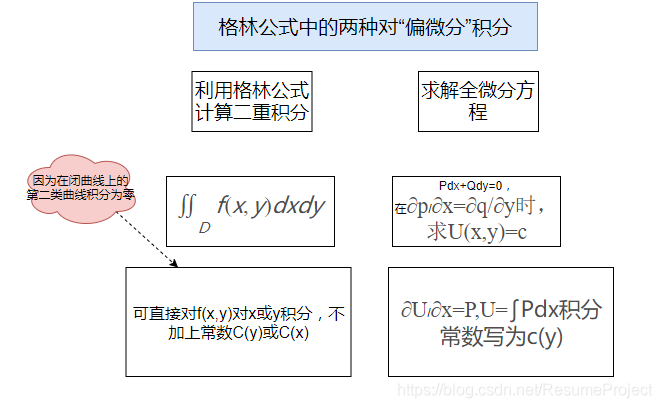
格林公式计算二重积分的例子:
∬ D e − y 2 d x d y ∬ D ∂ x e − y 2 ∂ x − ∂ 0 ∂ y d x d y = ∮ L x e − y 2 d y ( 化 为 了 第 二 类 曲 线 积 分 , 可 化 为 参 数 形 式 转 为 定 积 分 ∫ f ( t ) d t ) \iint_D e^{-y^2}dxdy\\ \iint_D\frac{ \partial xe^{-y^2}}{\partial x}-\frac{ \partial 0}{\partial y} dxdy\\ =\oint_L xe^{-y^2}dy(化为了第二类曲线积分,可化为参数形式转为定积分\int f(t)dt) ∬De−y2dxdy∬D∂x∂xe−y2−∂y∂0dxdy=∮Lxe−y2dy(化为了第二类曲线积分,可化为参数形式转为定积分∫f(t)dt)
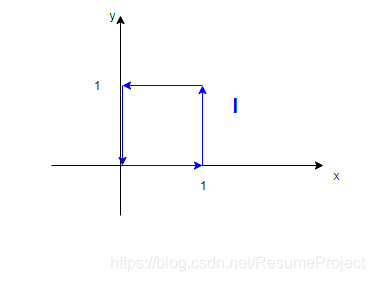
= ∮ L x e − y 2 d y = ∫ y = 0 x e − y 2 d y + ∫ x = 1 , y ∈ [ 0 , 1 ] x e − y 2 d y + ∫ y = 1 x e − y 2 d y − ∫ x = 0 , y ∈ [ 0 , 1 ] x e − y 2 d y = 0 + ∫ 0 1 e − y 2 d y + 0 + 0 =\oint_L xe^{-y^2}dy\\ =\int_{y=0} xe^{-y^2}dy+\int_{x=1,y\in[0,1]} xe^{-y^2}dy+\int_{y=1} xe^{-y^2}dy-\int_{x=0,y\in[0,1]} xe^{-y^2}dy\\ =0+\int_0^1 e^{-y^2}dy+0+0 =∮Lxe−y2dy=∫y=0xe−y2dy+∫x=1,y∈[0,1]xe−y2dy+∫y=1xe−y2dy−∫x=0,y∈[0,1]xe−y2dy=0+∫01e−y2dy+0+0
全微分方程的例子
求解: 2 x y + 1 y d x + y − x y 2 d y = 0 解 : 由 题 意 ∂ P ∂ y = ∂ Q ∂ x , 则 次 方 程 为 全 微 分 方 程 则 P = ∂ U ∂ x ⇒ U = x 2 + x y + c ( y ) Q = ∂ U ∂ y = − x y 2 + c ′ ( y ) c ( y ) = l n ∣ y ∣ + 1 , U = x 2 + x y + c ( y ) \frac{2xy+1}{y}dx+\frac{y-x}{y^2}dy=0\\ 解:由题意\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x},则次方程为全微分方程\\ 则P=\frac{\partial U}{\partial x} \Rightarrow U=x^2+\frac{x}{y}+c(y)\\ Q=\frac{\partial U}{\partial y}=-\frac{x}{y^2}+c'(y)\\ c(y)=ln|y|+1,U=x^2+\frac{x}{y}+c(y) y2xy+1dx+y2y−xdy=0解:由题意∂y∂P=∂x∂Q,则次方程为全微分方程则P=∂x∂U⇒U=x2+yx+c(y)Q=∂y∂U=−y2x+c′(y)c(y)=ln∣y∣+1,U=x2+yx+c(y)
这篇关于格林公式中对偏微分的积分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








