背景 求解真实问题中建模得到的非线性偏微分方程组, 尽可能少手写代码,如果用matlab, 可能的选项很有限。pdetoolbox有限元方法能够求解一些,但是要求对微分方程的类型以及pdetoolbox特有的书写方式非常熟悉,并能够把问题转为相应繁琐的格式; 早在Matlab 6.x版本的时候(已经10多年的历史了)出现了一个pdepe求解函数, 虽然同样繁琐,要写代码, 但对偏微分方程的知识

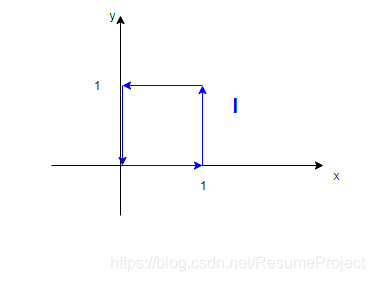
格林公式计算二重积分的例子： ∬ D e − y 2 d x d y ∬ D ∂ x e − y 2 ∂ x − ∂ 0 ∂ y d x d y = ∮ L x e − y 2 d y ( 化 为 了 第 二 类 曲 线 积 分 ， 可 化 为 参 数 形 式 转 为 定 积 分 ∫ f ( t ) d t ) \iint_D e^{-y^2}dxdy\\ \iint_D\frac{ \p