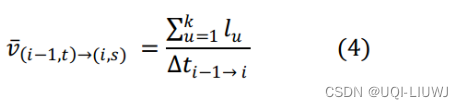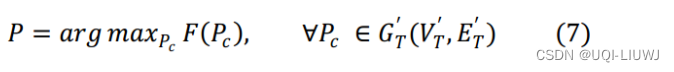论文笔记：Map-Matching for low-sampling-rate GPS trajectories（ST-matching）

2023-10-12 15:40
文章标签 笔记 论文 map low st gps sampling rate matching trajectories

本文主要是介绍论文笔记：Map-Matching for low-sampling-rate GPS trajectories（ST-matching），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

ACM-GIS 2019

1 Intro

  • 将GPS数据和地图路网数据匹配
  • 提出全局地图匹配算法ST-matching（类似于HMM的思路）
    • 考虑了道路网络的空间几何和拓扑结构
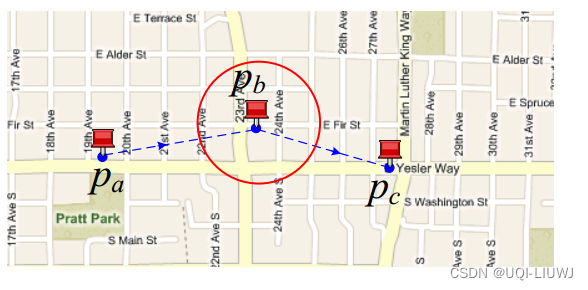
      • 如果不考虑拓扑关系，直接进行matching的话，由于GPS信号的不准，可能轨迹会和实际情况差很多
    • 考虑的轨迹的速度因素
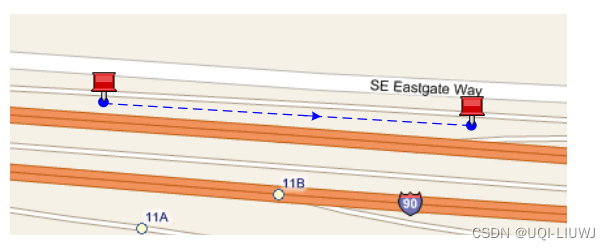
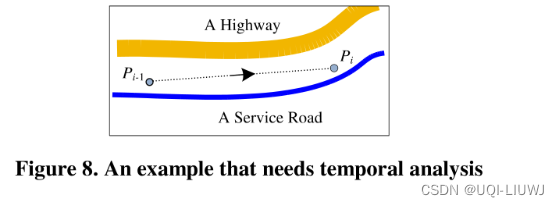
      • 比如一条高速、一条公路平行，那么如果不考虑速度的话，这样一组GPS信号应该把它放到高速上？还是公路上？

2 问题描述 

 2.1 GPS日志

  • 一系列GPS点的集合L=\{p_1,p_2,\cdots,p_n\}
    • 每个GPS的点包括经度、维度、时间戳

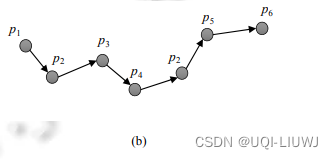
2.2 GPS轨迹

  • 一条GPS轨迹T是一个GPS点的序列
    • 一条轨迹任意两个相邻点之间的时间间隔不超过ΔT（一个阈值）

2.3 路段

  • 一个路段 e 是一条有向边,具有编号 e.id、行驶速度 e.v、长度 e.l、开始点 e.start、结束点 e.end 和中间点列表.
  • 一条道路可以包含多个路段

2.4 路网

一个有向图 G(V,E)

2.5 路径

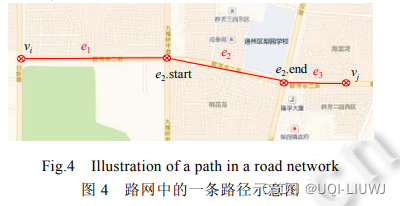
  • 给定路网 G 中的两个顶点 vi,vj,一条路径 P 是始于 vi 止于 vj 的一组连接的路段e_1 \rightarrow e_2 \rightarrow \cdots \rightarrow e_n
    • e_1=v_i,e_n=v_j

2.6 路网匹配

给定未加工的 GPS 轨迹 T 和路网 G(V,E),从 G 中寻找路径 P（实际路径匹配轨 迹 ）

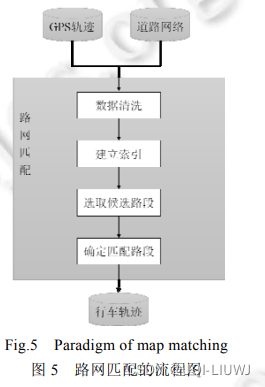
3 ST-matching

3.0 和HMM的概念对应

  • 观测状态——从 GPS 设备中得到的位置信息(经度、纬度)
  • 隐藏状态——拥有 GPS 设备的物体(车、人等)实际所在的位置
  • 观测状态概率（输出概率）——观测的 GPS 样本点离候选路段越近,这个样本点在这个路段上的概率就越大.
  • 状态转移概率——隐藏状态之间的转换概率

3.1 确定候选点

  • 给定一条确定轨迹T=p_1\to p_2\to p_3\to\dots\to p_n
    • 对每一个点pi​，在半径为r的范围内搜索该路段的候选集
    • 然后计算候选点，候选点是pi​对这些路段的投影

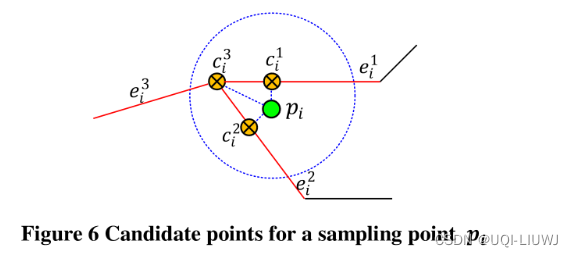
每一个点找到这样的一个候选点集合，得到候选点图

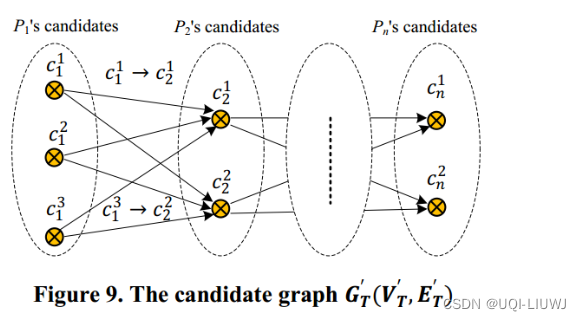
3.2 空间分析

3.2.1 观测状态概率（输出概率）

  • N(c_i^j)=P(c_i^k|o_i)=\frac{1}{\sqrt{2 \pi} \sigma}e^{-\frac{||c_i^k-o_i||^2}{2\sigma^2}}
    • oi是第i个观测点
    • c_i^k是第i个观测点的第k个candidate
    • ||c_i^k-o_i||^2=dist(c_i^k,o_i)
    • 时刻 t 的观测点与候选点之间的距离越小,这个候选点是真正的实际点的概率就越大
    • ——这里根据经验选择零均值、std为20的正态分布
  • 观测概率不考虑前后GPS定位点，所以容易出现误匹配

    3.2.2 空间分析函数

    • 如下图，粗实线代表高速公路，细的垂线代表本地道路。
    • 采样点（观测点）pi​距离第一个候选点比较近，但是如果我们知道前一个采样点和后一个采样点在高速路上，所以理论上应该匹配到第2个采样点
  •  
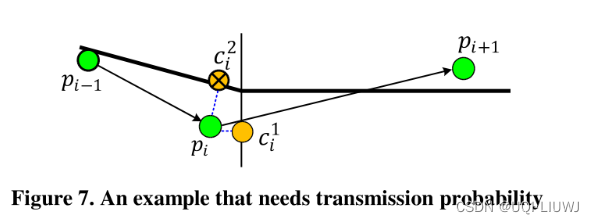
    • ST-matching将空间拓扑关系也考虑了进来：【空间传递概率】
      • V(c_i \rightarrow c_j)=\frac{||o_{t+1}-o_t||_{euclidean}}{||c_i-c_j||_{route}}
        • 根据t+1和t时刻观测值和候选值的信息，推测从t时刻的观测值ot到t+1时刻的观测值o_{t+1}之间的真实路径是ci到cj最短路径的可能性
        • 观测值之前的距离/候选点之间的距离

  •  空间分析函数

    • F_s(c_i \rightarrow c_j)=N(c_j) \cdot V(c_i \rightarrow c_j)

    • 结合了观测概率【几何信息】和传递概率【拓扑信息】

    • 如果没有N(cj)的话，那么为了Fs越大越好，||ci-cj||越小越好，最后就会选择距离p_{i-1}路径距离最近的candidate了

3.3 时间分析

  • 如果只使用空间分析的话，大部分真实路径都可以match，但是就如intro中说的那样，有一些情况无法处理：

  • 这时候就需要时间传递概率（速度传递概率）

    • F_t(c_i \rightarrow c_j)=\frac{\sum_{1}^k(e_u' \cdot v \times \bar{v_ij})}{\sqrt{\sum_1^k(e_u' \cdot v)^2} \times \sqrt{\sum_1^k( \bar{v_ij})^2}}
      • 时间分析函数
      • 用余弦距离来衡量从候选点ci到候选点cj之间的平均速度，和路段速度约束之间的相似度
      • ci到cj之间的路径被定义为一个路段列表：[e_1'\cdots e_k']
        • 每个路段的速度约束为e_u' \cdot v
      • \bar{v_{ij}}是ci到cj的平均速率

3.4 获取路径

  • 将空间分析函数和时间分析函数结合，得到时空分析函数

  • 真实路径T匹配的最优路径P为使得F(Pc)最大的候选点路径集合Pc

3.4.1 伪代码

 

3.5 本地ST-matching

  •  ST-Matching是全局算法，但是实际中不可能都给出完整路径
  • ——>local ST-matching使用轨迹上的滑动窗口
    • 局部候选图是轨迹T的一个子集
    • 计算方式和全局算法一样
    • 计算一个滑动窗口中的局部候选图后，移动滑动窗口，计算后续的滑动窗口
  • 将轨迹划分为窗口可以：
    • 减少平均延迟
    • 节省用于在线处理的存储空间
    • 但不一定会加快整体处理时间，因为ST匹配算法最昂贵的部分是最短的路径计算（空间分析函数中V(c_i \rightarrow c_j)=\frac{||o_{t+1}-o_t||_{euclidean}}{||c_i-c_j||_{route}}的||c_i-c_j||_{route}）

  • 为了降低计算复杂度，可以保留到目前为止，得分最高的l个候选点（而不是所有的候选点）
    • ——>减少下一个采样点需要计算的最短路径的pair数量
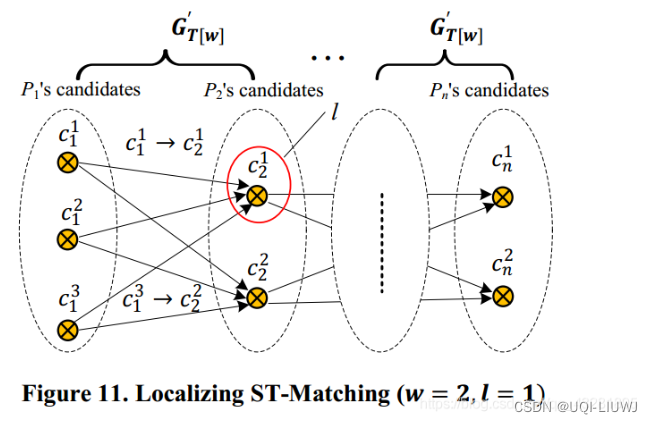
    • 当l=1时，退化成增量算法

  • w=2——>滑动窗口为2，每次只考虑两个时刻组成的子路段
  • l=1——>每次只保留F值最高的一个候选点，后续st-matching也只会考虑这一个点

 3.6 复杂度

【推导过程我不确定，请评论区批评指正】

记轨迹中的采样点个数为n、路网中路段个数为m，每个采样点最多有k个候选点

  • 每个点找候选点：O(n)
  • 候选点图GT中最多有(n-1)k^2条边
    • 相邻的两个采样点对应的候选点之间最多k^2条边
    • n个采样点，有n-1个间隔
  • 每一条边计算F(c_t,c_{t+1})需要的开销
    • Fs：V(c_i \rightarrow c_j)=\frac{||o_{t+1}-o_t||_{euclidean}}{||c_i-c_j||_{route}}
      • 计算ci和cj的最小路径长度，使用堆优化的迪杰斯特拉算法，复杂度是O(mlogm)
    • Ft:F_t(c_i \rightarrow c_j)=\frac{\sum_{1}^k(e_u' \cdot v \times \bar{v_ij})}{\sqrt{\sum_1^k(e_u' \cdot v)^2} \times \sqrt{\sum_1^k( \bar{v_ij})^2}}
      • 这个不怎么占复杂度，可以视为O(m)
    • ——>构建候选点图需要的复杂度O(nk^2mlogm)【 algorithm 1】（n-1和n没有区别）
  • 进行地图matching需要的开销
    • 每一条边只需要遍历一次
      • ——>复杂度是O(nk^2)
  • ——>总的复杂度是O(nk^2mmlogm+nk^2)

4 实验

4.1 实验配置

4.1.1 路网

  • 北京的路网
    • 58624个点
    • 130714条路段

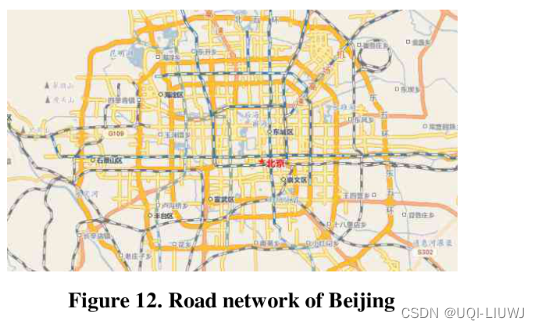
4.1.2 数据

  • 人工数据
    • 首先随机选择两个点
      • 在这两个点之前选择前K段的路径
      • 在这K段路径中，随机选择一条，记作G: e_1,e_2,\cdots,e_n
      • 指定一个采样间隔k'，从G中以这个间隔挑选点e_1,e_{1+k'}.\cdots,e_{1+mk'}
    • 用这些挑选出来的点match轨迹，看和ground-truth一不一样
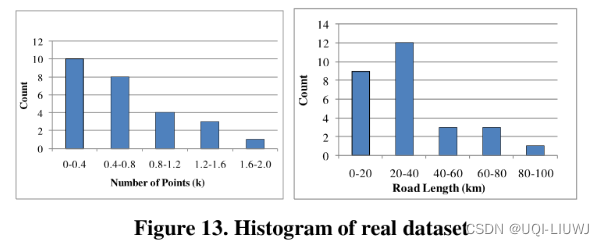
  • 真实数据
    • 从GoeLife系统中采集28条轨迹，这些轨迹都手工标注的label（作为ground truth）

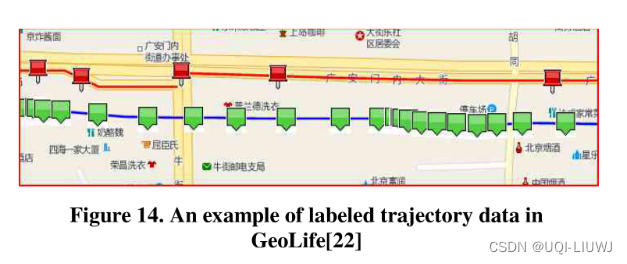    •  绿色+蓝色是GPS轨迹，红色是用户的实际轨迹

4.2 评估标准 

 4.3 结论

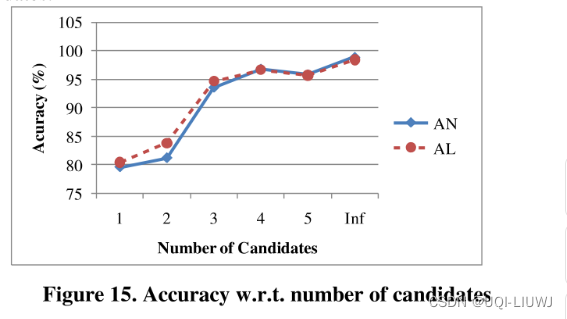
4.3.1 候选点数量的影响

准确率 

 运行时间

4.3.2 S-matching 和 ST-matching

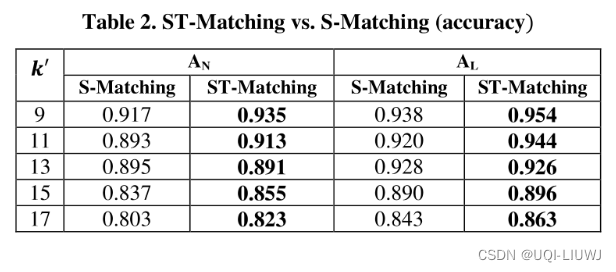
 4.3.3 和Baseline的比较

AFD——最小平均Frechet距离

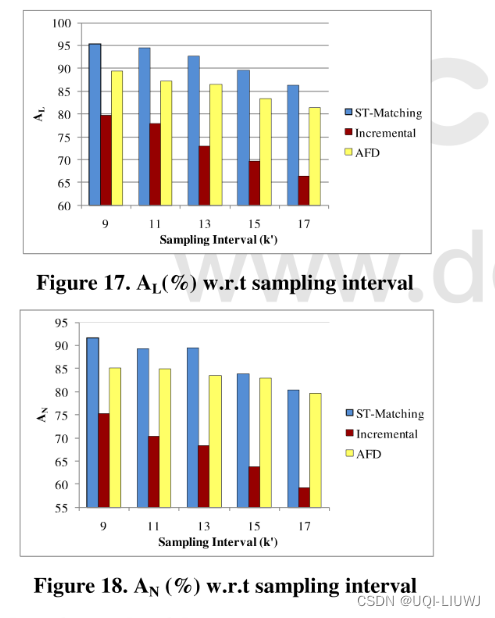
这篇关于论文笔记：Map-Matching for low-sampling-rate GPS trajectories（ST-matching）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/196805。

相关文章

AI hospital 论文Idea

AI hospital 论文Idea

一、Benchmarking Large Language Models on Communicative Medical Coaching: A Dataset and a Novel System论文地址含代码 大多数现有模型和工具主要迎合以患者为中心的服务。这项工作深入探讨了LLMs在提高医疗专业人员的沟通能力。目标是构建一个模拟实践环境，人类医生（即医学学习者）可以在其中与患者代理进行医学
阅读更多...
【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系列文章目录 监督学习：参数方法 【学习笔记】 陈强-机器学习-Python-Ch4 线性回归 【学习笔记】 陈强-机器学习-Python-Ch5 逻辑回归 【课后题练习】 陈强-机器学习-Python-Ch5 逻辑回归（SAheart.csv） 【学习笔记】 陈强-机器学习-Python-Ch6 多项逻辑回归 【学习笔记 及 课后题练习】 陈强-机器学习-Python-Ch7 判别分析 【学
阅读更多...
系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

本章知识考点：         第20课时主要学习通信系统架构设计的理论和工作中的实践。根据新版考试大纲,本课时知识点会涉及案例分析题(25分),而在历年考试中,案例题对该部分内容的考查并不多,虽在综合知识选择题目中经常考查,但分值也不高。本课时内容侧重于对知识点的记忆和理解,按照以往的出题规律,通信系统架构设计基础知识点多来源于教材内的基础网络设备、网络架构和教材外最新时事热点技术。本课时知识
阅读更多...
论文翻译：arxiv-2024 Benchmark Data Contamination of Large Language Models: A Survey

论文翻译：arxiv-2024 Benchmark Data Contamination of Large Language Models: A Survey

Benchmark Data Contamination of Large Language Models: A Survey https://arxiv.org/abs/2406.04244 大规模语言模型的基准数据污染：一项综述 文章目录 大规模语言模型的基准数据污染：一项综述摘要1 引言 摘要 大规模语言模型（LLMs），如GPT-4、Claude-3和Gemini的快
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划 非线性规划1. 模型原理1.1 非线性规划的标准型1.2 非线性规划求解的Matlab函数 2. 典型例题3. matlab代码求解3.1 例1 一个简单示例3.2 例2 选址问题1. 第一问 线性规划2. 第二问 非线性规划 非线性规划 非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。2
阅读更多...
【C++学习笔记 20】C++中的智能指针

【C++学习笔记 20】C++中的智能指针

智能指针的功能 在上一篇笔记提到了在栈和堆上创建变量的区别，使用new关键字创建变量时，需要搭配delete关键字销毁变量。而智能指针的作用就是调用new分配内存时，不必自己去调用delete，甚至不用调用new。 智能指针实际上就是对原始指针的包装。 unique_ptr 最简单的智能指针，是一种作用域指针，意思是当指针超出该作用域时，会自动调用delete。它名为unique的原因是这个
阅读更多...
Collection List Set Map的区别和联系

Collection List Set Map的区别和联系

Collection List Set Map的区别和联系 这些都代表了Java中的集合，这里主要从其元素是否有序，是否可重复来进行区别记忆，以便恰当地使用，当然还存在同步方面的差异，见上一篇相关文章。 有序否 允许元素重复否 Collection 否 是 List 是 是 Set AbstractSet 否
阅读更多...
查看提交历史 —— Git 学习笔记 11

查看提交历史 —— Git 学习笔记 11

查看提交历史 查看提交历史 不带任何选项的git log-p选项--stat 选项--pretty=oneline选项--pretty=format选项git log常用选项列表参考资料 在提交了若干更新，又或者克隆了某个项目之后，你也许想回顾下提交历史。 完成这个任务最简单而又有效的 工具是 git log 命令。 接下来的例子会用一个用于演示的 simplegit
阅读更多...
记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 文章目录 文件的状态三个区域检查当前文件状态跟踪新文件取消跟踪（un-tracking）文件重新跟踪（re-tracking）文件暂存已修改文件忽略某些文件查看已暂存和未暂存的修改提交更新跳过暂存区删除文件移动文件参考资料 咱们接着很多天以前的 取得Git仓库 这篇文章继续说。 文件的状态 不管是通过哪种方法，现在我们已经有了一个仓库，并从这个仓
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2