本文主要是介绍深度优先（DFS) （例子：全排列，迷宫，pta龙龙送外卖），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
深度搜索是一种计算机算法，用于在图或树等数据结构中查找目标节点。深度搜索从一个节点出发，依次遍历其所有子节点，直到找到目标节点或遍历完所有节点。如果找到目标节点，则搜索结束；如果遍历完所有节点仍未找到目标节点，则搜索失败。深度搜索通常使用递归实现，通过堆栈管理遍历的节点。深度搜索常用于解决迷宫、棋盘等问题，也是其他算法的核心组成部分，如搜索算法、动态规划等。
模型：
void dfs(int step)
{
判断边界
for(int i=1;i<=n;i++)//尝试每种可能
{
dfs(step+1)；//继续下一步
}
reutn；//返回
}
深度优先搜索（DFS）全排列的基本思路是对于一个长度为n的数组，从第1个位置开始（即起始状态），对于每个未选择的数字，在当前的位置上进行一次选择，然后向下递归直到找到一个完整的排列，然后回溯到当前状态，再选择下一个未选择的数字进行搜索。
#include<iostream>//深度优先搜索，全排列为例子
using namespace std;
int book[100];//标记
int n;
int a[100];
void dfs(int step)
{int i;if (step == n + 1)//判断边界{for (int i = 1; i <= n; i++)cout << a[i]<<" ";cout << endl;return;}for (int i = 1; i <= n; i++)//每种可能{if (book[i] == 0){a[step] = i;book[i] = 1;dfs(step + 1);//继续下一步book[i] = 0;}}return;
}
int main()
{cin >> n;dfs(1);
}
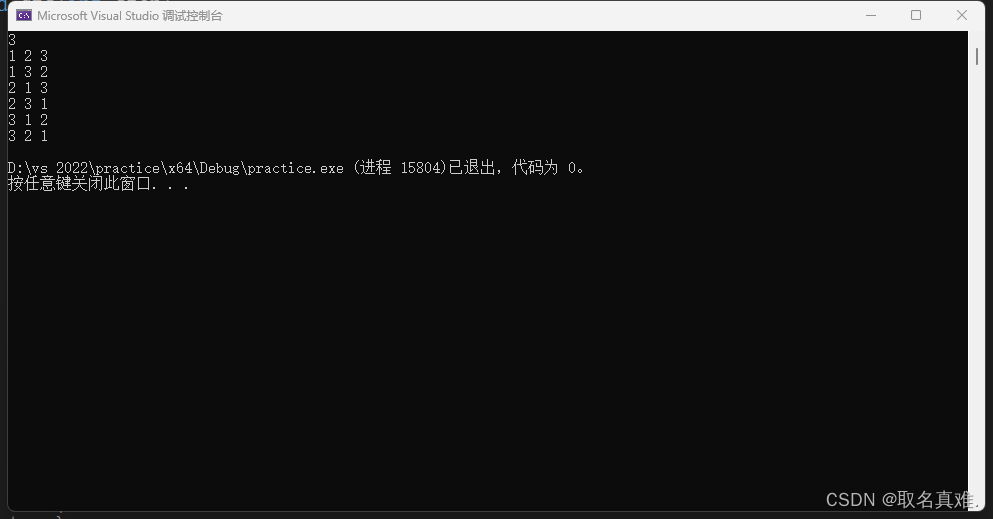深度搜索算法可以用于解决迷宫问题。将迷宫抽象成一个矩阵，每个格子表示一个节点。将起点节点入栈，然后遍历其所有相邻节点。如果相邻节点是通路，则将其入栈，并在矩阵中标记为已访问。如果相邻节点是终点，则搜索结束；如果所有相邻节点都是墙，或者已经访问过，则回溯到上一步节点。重复以上步骤，直到遍历完所有节点或者找到终点。
#include<iostream>//深度优先搜索，迷宫最短路径问题
using namespace std;
int book[51][51];//标记是否走过
int n,m,q,p,x,y;
int a[51][51];
int min1 = 9999;
int next1[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };//右，下，左，上四个方向
void dfs(int x,int y,int step)
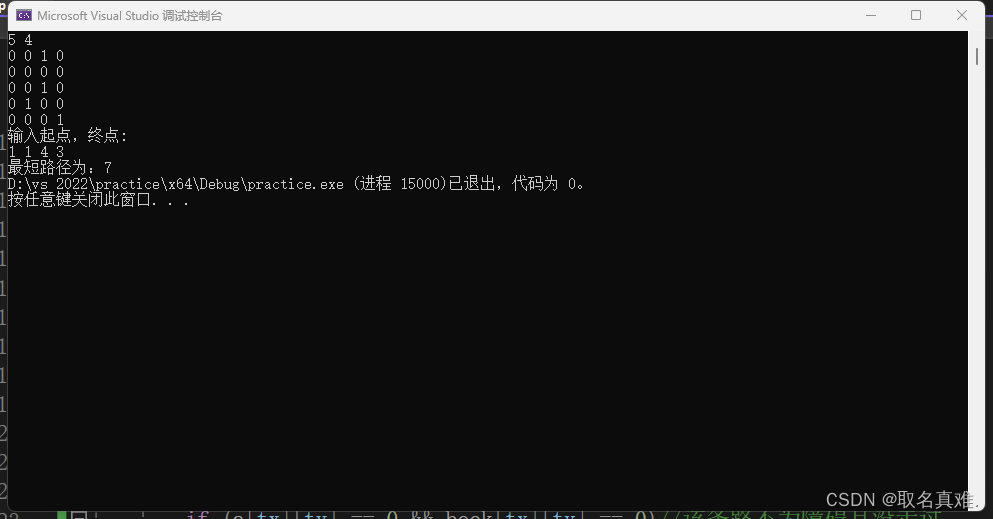
{int tx, ty;if (x == q && y == p)//走到终点{if (step < min1)min1 = step;return;}for (int k = 0; k < 4; k++)//向四个方向都走{tx = x + next1[k][0];ty = y + next1[k][1];if (tx<1 || tx>n || ty<1 || ty>m)continue;if (a[tx][ty] == 0 && book[tx][ty] == 0)//该条路不为障碍且没走过{book[tx][ty] = 1;//标记已走过dfs(tx, ty, step + 1);book[tx][ty] = 0;//尝试结束，取消标记}}return;
}
int main()
{cin >> n >> m;//迷宫规模for (int i = 1; i <= n; i++)//0为可走通路for (int j = 1; j <= m; j++)cin >> a[i][j];//输入迷宫cout << "输入起点，终点:" << endl;cin >> x >> y >> q >> p;//输入起点，终点book[x][y] = 1;//起点默认走过dfs(x,y,0);cout <<"最短路径为："<< min1;
}
龙龙是“饱了呀”外卖软件的注册骑手，负责送帕特小区的外卖。帕特小区的构造非常特别，都是双向道路且没有构成环 —— 你可以简单地认为小区的路构成了一棵树，根结点是外卖站，树上的结点就是要送餐的地址。
每到中午 12 点，帕特小区就进入了点餐高峰。一开始，只有一两个地方点外卖，龙龙简单就送好了；但随着大数据的分析，龙龙被派了更多的单子，也就送得越来越累……
看着一大堆订单，龙龙想知道，从外卖站出发，访问所有点了外卖的地方至少一次（这样才能把外卖送到）所需的最短路程的距离到底是多少？每次新增一个点外卖的地址，他就想估算一遍整体工作量，这样他就可以搞明白新增一个地址给他带来了多少负担。
输入格式:
输入第一行是两个数 N 和 M (2≤N≤105, 1≤M≤105)，分别对应树上节点的个数（包括外卖站），以及新增的送餐地址的个数。
接下来首先是一行 N 个数，第 i 个数表示第 i 个点的双亲节点的编号。节点编号从 1 到 N，外卖站的双亲编号定义为 −1。
接下来有 M 行，每行给出一个新增的送餐地点的编号 Xi。保证送餐地点中不会有外卖站，但地点有可能会重复。
为了方便计算，我们可以假设龙龙一开始一个地址的外卖都不用送，两个相邻的地点之间的路径长度统一设为 1，且从外卖站出发可以访问到所有地点。
注意：所有送餐地址可以按任意顺序访问，且完成送餐后无需返回外卖站。
输出格式:
对于每个新增的地点，在一行内输出题目需要求的最短路程的距离。
输入样例:
7 4
-1 1 1 1 2 2 3
5
6
2
4
输出样例:
2
4
4
6
注意：把该题看出树结构，深度搜索
1、该题最主要是从下往上，搜索父亲节点，用dis[]储存该点到树根的距离，a[]储存该点的父亲节点。
2、该题dfs判断边界是：搜索到树根或者搜索到父亲节点已经经过两种情况，返回的是到树根或者到父亲节点的来回距离。
3、剩下返回新增一个点需要增加的距离。
4、因为不用返回树根，所以挑最长的距离最后走，不用返回。所以最后结果为sum-maxl。
#include<iostream>
using namespace std;
int n, m,sum=0;
int a[11000];//储存树
int dis[11000] = { 0 };
int maxl;//最长路径
int dfs(int x, int step)
{if (a[x] == -1 || dis[x]){maxl = max(maxl, dis[x] + step);//取最大深度return step * 2;}int res = dfs(a[x], step + 1);//搜索父亲节点，深度加一dis[x] = dis[a[x]] + 1;//该点到树根距离为父亲节点到树根距离加一return res;
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];while (m--){int x;cin >> x;sum+=dfs(x, 0);cout << sum - maxl << endl;}
}这篇关于深度优先（DFS) （例子：全排列，迷宫，pta龙龙送外卖）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
