本文主要是介绍DATA VIS Lab—Network visualization(1)周结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
@DATA VIS Lab—Network visualization(1)
第四周
2019.9.25
基于社团结构节点重要性的网络可视化压缩布局
*(论文来源于万方数据库,转载请附上原文出处链接和本声明)
Idea:
1.本文中的一个创新点在于将力导引布局算法与网络社团结构特征相结合,提出一种基于社团结构节点重要性的网络可视化压缩布局方法(Compression Layout Method for Network Visualization Based on the
Node Importance for CommunityStructure)。该方法首先采用 Louvain 算法对网络进行多粒度社团结构划分;然后,计算社团结构中节点的拓扑势评估社团结构内部的节点重要性,并将社团内部节点分为 3 类,通过保留社团中的重要节点,合并边缘节点,实现社团结构压缩。
文中提到的几个算法:
2. KK(Kamada-Kawai)算法 [8] 在弹簧模型的基础上引入胡克定律,根据节点受力状态计算系统能量,将节点最优布局问题转化为系统能量最小化的求解问题,使布局过程的收敛速度有了明显的增加。
-
DH(Davidson-Harel)算法中考虑了节点位置、连边长度和连边交叉等多种美学标准的约束来构建能量函数,通过能量函数模型参数可达到不同的布局效果。
-
多粒度社团结构探测是本文中用作网络可视化布局的主要算法,在其中起到主要作用的是Louvain 算法,其中起到判断作用的是模块度是刻画网络中社团划分质量的重要指标之一,其计算公式是:
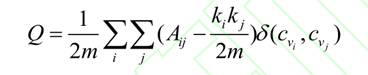
基于模块度优化的社团结构探测算法属于凝聚算法的一种,它通过优化模块度增益函数不断地凝聚节点,最终获得社团结构划分结果。文献将模块度增量数定:
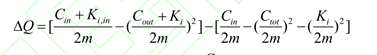
节点拓扑势的大小描述了网络拓扑中的某个节点受自身和近邻节点共同影响具有的势值。类似地,对于一个给定的社团 ( , )C CC V E = ,社团中任意一个节点
iv 的拓扑势的计算公式为:
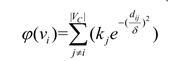
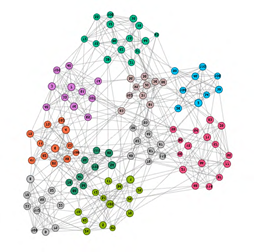
问题:结点压缩实现的方法为什么以边缘节点CCV 设置替代节点?
上周:1.尝试实现论文中关于gephi结点社团结构压缩算法的布局操作
2.阅读论文《基于社团结构节点重要性的网络可视化压缩布局》
3.继续学习python科学计算库(numpy等)
4.学习相关布局算法和公式
问题:1.在进行结点布局操作时有部分的功能还没办法达到效果
2.论文中有些算法的原理还没办法完全理解(kk算法)
3.计算库的一些功能还没有掌握
下周计划:
-
继续尝试实现论文中未实现的功能
-
查找相关webgl编程的相关实例,进行初步了解
-
学习python的图形绘制库(matplotlib)
这篇关于DATA VIS Lab—Network visualization(1)周结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





