【最优传输论文十四】2019 CVPR-Sliced Wasserstein Discrepancy for Unsupervised Domain Adaptation

1.motivation

无监督域适应大部分工作都集中在建立源域和目标域的特征分布之间的直接对齐。这种对齐涉及最小化模型学习到的特征分布的一些距离度量。更复杂的方法使用对抗性训练，通过在特征级、像素级或输出级跨域调整表示，从而提高分布之间对齐的质量。

在MCD中提出了一种基于网络内对抗学习的方法，该方法包含一个特征生成器和两个(特定任务)分类器，该方法使用特定任务的决策边界来对齐源样本和目标样本。然而存在一些局限性。例如，它们的差异损失(MCD中为L1)只有在分类器的两个输出概率度量重叠时才有用。

受MCD中的框架的启发，作者将精力集中在改进差异度量上，差异度量在这种基于网络内对抗性学习的方法中起着核心作用。作者将无监督域自适应的两个不同概念联系起来:通过使用特定于任务的决策边界和Wasserstein度量来实现域之间的特征分布对齐。本文提出的切片Wasserstein差异(SWD)方法旨在通过使用Wasserstein度量来最小化在任务特定分类器之间移动边际分布的成本，捕捉特定任务分类器输出之间的不相似性的自然概念。它提供了一个几何上有意义的指导，以检测远离源支持的目标样本，并以端到端可训练的方式实现有效的分布对齐。在实验中，作者验证了该方法在数字和符号识别、图像分类、语义分割和目标检测方面的有效性和通用性。

本文几个关键贡献:

(1)通过最优传输理论(即Wasserstein距离)和任务特定决策边界，提出了一种新的原则性方法来对齐域之间的特征分布。

(2)使用切片Wasserstein差异(Wasserstein度量的变分公式)实现有效的端到端训练。

(3)有效地利用通过以对抗的方式优化切片Wasserstein差异创建的底层流形的几何形状。

(4)该方法在多个任务中推进了最新技术，可以很容易地应用于任何领域自适应问题，如图像分类、语义分割和目标检测。

2.Related Work

大量的无监督域自适应方法旨在通过各种统计矩匹配技术，通过学习域不变特征表示来减少源域和目标域之间的差距。一些方法利用最大平均差异(MMD)来匹配深度神经网络中某些层的隐藏表示。其他方法使用中心矩差异(CMD)方法来显式匹配高阶矩的每个阶和每个隐藏坐标。自适应批归一化(Adaptive batch normalization, AdaBN)也被提出用于调节跨域网络的所有批归一化层中的统计信息。

另一类策略通过利用gan的对抗学习行为来解决领域适应问题。这种技术首先用于特征级，训练一个域鉴别器来正确分类每个输入特征的域，训练特征生成器来欺骗域鉴别器，从而使得到的特征分布成为域不变的。随后，将该技术应用于像素级，在原始输入空间中进行分布对齐，将源域转换为目标域的“样式”，并获得在转换后的源数据上训练的模型。最近，该技术被用于输出级，假设输出空间包含类似的空间结构，用于某些特定的任务，如语义分割。因此，[70]中的方法通过输出空间中的对抗性学习来对齐像素级的ground truth。

相比之下，MCD提出通过显式地使用特定于任务的分类器作为判别器来对齐分布。该框架最大化两个分类器输出之间的差异，以检测源支持之外的目标样本，然后最小化差异，以生成相对于决策边界的源支持内的特征表示。这种方法不是通过启发式假设来对齐特征、输入或输出空间中的流形，而是侧重于直接重塑确实需要重塑的目标数据区域。

Wasserstein度量是由最优传输理论引起的概率度量的自然几何，已经在图像检索、基于颜色的风格转移和图像扭曲等多个领域进行了研究。这是因为即使在分布的支持不重叠的情况下，它也具有几何意义的距离度量。

在领域自适应方面，Courty等[10]首先学习具有类规则性的源样本和目标样本匹配的运输计划。JDOT方法通过综合考虑类规则性和特征分布，学习从源到目标的输入空间映射。DeepJDOT方法在JDOT的基础上进一步改进，在深度神经网络层中使用更具判别性的特征表示联合匹配特征和标签空间分布。然而，这些方法显式地在标签空间中强制源样本和目标样本之间进行一对一的映射，这在很大程度上限制了平衡的源-目标对不可用时的实际使用。当一个数据样本具有结构化的输出空间(如逐像素语义分割)时，如何将这些方法扩展到更通用的任务中也不清楚。

在本文中提出了一个原则性框架来结合两个强大的概念:特定任务决策边界的分布对齐和Wasserstein距离。Wasserstein度量作为任务特定分类器之间可靠的差异度量，它直接度量源样本对目标样本的支持程度，而不是在标签空间中产生显式的一对一映射。Wasserstein差异的变分版本进一步提供了直观且具有几何意义的梯度，以有效地联合训练框架中的特征生成器和分类器。

3.Method

首先在3.1节介绍无监督域自适应设置。其次，简要回顾3.2节中最优运输的概念。最后，在3.3节中详细介绍了如何使用切片Wasserstein差异来训练所提出的方法。

3.1. Framework Setup

给定从源集{xs, ys}中提取的输入数据xs和相应的ground truth ys，以及从目标集xt中提取的输入数据xt，无监督域自适应的目标是建立从标记的源集到未标记的目标集的知识转移。当两个数据分布Xs和Xt足够接近时，人们可以简单地关注最小化联合概率分布P(Xs, Ys)的经验风险。但是，当这两个分布有很大的不同时，仅在源信息上优化模型会导致较差的泛化性。

根据最大分类器差异(Maximum Classifier Discrepancy, MCD)框架，本文训练了一个特征生成器网络G和分类器网络C1和C2，它们分别取G生成的特征响应，并产生相应的logits p1(y|x)， p2(y|x)(如图1所示)。

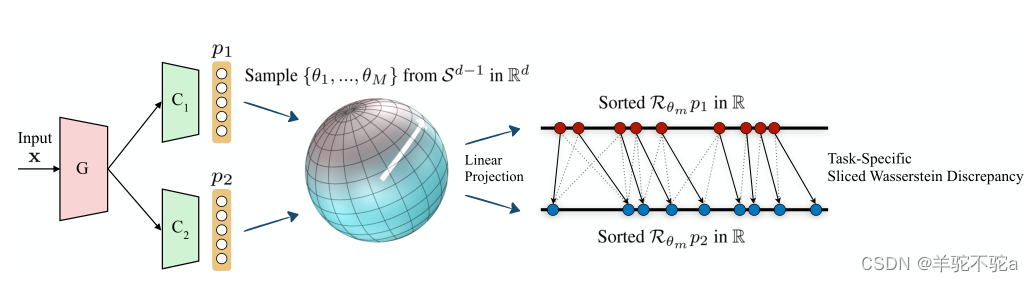
 图1:提出的切片Wasserstein差异(SWD)计算的示意图。SWD旨在捕捉任务特定分类器C1和C2在Rd中的概率测度p1和p2的不同之处，它们从特征生成器g中获取输入。SWD通过使用单位球面上均匀测度的径向投影的Wasserstein度量的变分公式直接实现端到端训练，为检测远离源支持的目标样本提供了几何上有意义的指导。详情请参阅第3.3节。

优化过程包括三个步骤:

（1）在源域{Xs, Ys}上训练生成器G和分类器(C1, C2)对源样本进行正确分类或回归;

 其中Ls可以是任何损失函数，如交叉熵损失或均方误差损失。

（2）冻结生成器G的参数，更新分类器(C1, C2)，使两个分类器在目标集Xt上的输出差异最大化，识别出不在任务特定决策边界支持范围内的目标样本，

其中为差异损失(MCD中的L1)。Ls(Xs, Ys)也添加到此步骤中以保留来自源域的信息。

（3）冻结两个分类器的参数并更新生成器G，使两个分类器在目标集Xt上的输出差异最小,

这一步使目标特征流形更接近源。 

 3.2. Optimal Transport and Wasserstein Distance

在上述MCD框架中，域自适应的有效性完全取决于差异损失的可靠性。没有差异损失的学习，基本上是放弃训练过程中的第二步和第三步，只是源域上的监督学习。

与其他流行的概率度量(如总变异距离、Kullback-Leibler散度和Jensen-Shannon散度)单独比较逐点直方图嵌入相比，Wasserstein距离考虑了概率空间底层几何的性质，它甚至能够比较不共享支持的分布度量。由于Wasserstein距离的优势，利用这个度量来测量本文方法中的差异。

设Ω为概率空间，μ， ν为P(Ω)中的两个概率测度，则Monge问题寻求代价最小的传输映射T: Ω→Ω

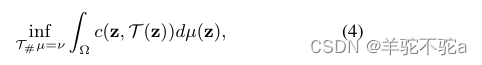
其中T#µ= ν表示从u到v所有Borel子集和c: Ω x Ω→R+是一个测地线度量，可以是线性的，也可以是二次的。然而，解T *可能并不总是存在，因为假设概率测度没有分裂，例如当把狄拉克测度推到非狄拉克测度时。

Kantorovitch提出了一个简化版的Eq 4，寻求一个联合概率分布γ∈P(Ω × Ω)的运输计划，使得

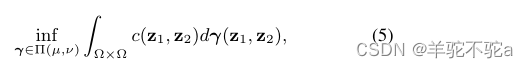
π1和π2表示的两个边缘投影Ω×Ω到Ω。解γ *称为最优运输计划或最优耦合。

 当q≥1时，定义P(Ω)中µ与ν之间的q- wasserstein距离为

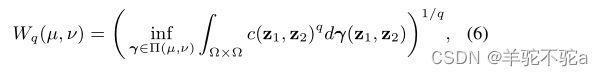
 这是由最优运输方案引起的最小成本。本文使用1-Wasserstein距离，也称为推土机距离(EMD)。

3.3. Learning with Sliced Wasserstein Discrepancy

在本文将1-Wasserstein距离应用于第3.1节中描述的领域适应框架。在上述框架的步骤2和步骤3中，使用具有几何意义的1-Wasserstein距离作为差异度量。在实践中，考虑分类器logits p1(y|x)和p2(y|x)的离散版本。计算W1(p1, p2)需要通过求解线性规划问题获得最优输运耦合γ *，这是低效的。虽然过去已经提出了各种优化方法，但如何以端到端可训练的方式直接优化W1(p1, p2)还不清楚。

为了充分利用两个概念的优势-通过利用任务特定的决策边界来调整源和目标的分布，并结合Wasserstein差异，它具有良好的随机梯度下降训练的能量景观，本文通过使用切片Wasserstein差异将W1(p1, p2)集成到我们的框架中。分类器输出p1和p2之间沿径向投影的1-Wasserstein距离的一维变分公式。

由于[53]定义了离散测度的切片重心，我们将切片1-Wasserstein差异(SWD)定义为

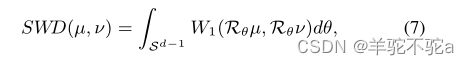
 其中，Rθ表示概率测度μ或ν上的一维线性投影运算，θ是Rd中单位球上的均匀测度，使得。这样，计算切片Wasserstein差异就相当于求解几个具有封闭解的一维最优输运问题。

具体地说，设α和β是对N个样本的N个一维线性投影排序的排列，使用排序算法使得时, 和，那么最小化这种一维Wasserstein距离的最优耦合γ∗只需将分配给。对于离散概率测度，我们的SWD可以写成:

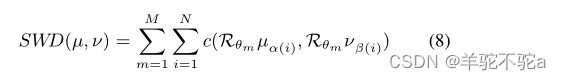
 是对于M随机抽样θ，c为二次损失。本文提出的SWD本质上是原始Wasserstein距离的变分版本，但其计算成本只是原始Wasserstein距离的一小部分。更重要的是，由于SWD的接近形式特征，它是可微的，因此可以将重点放在使用最优传输作为可靠的保真度度量来指导特征生成器和分类器的优化。在算法1中总结了本文的框架，并在图1中说明了SWD计算。

swd_pytorch.py

from __future__ import print_function
import argparse
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import imageio
import platform
if platform.system() == 'Darwin':import matplotlibmatplotlib.use('TkAgg')def toyNet():# Define network architectureclass Generator(nn.Module):def __init__(self):super(Generator, self).__init__()self.l1 = nn.Linear(2, 15)self.l2 = nn.Linear(15, 15)self.l3 = nn.Linear(15, 15)self.relu = nn.ReLU(inplace=True)for m in self.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight) #对权重进行均匀分布初始化nn.init.constant_(m.bias, 0)    #偏置初始化为0def forward(self, x):x = self.relu(self.l1(x))x = self.relu(self.l2(x))x = self.relu(self.l3(x))return xclass Classifier1(nn.Module):def __init__(self):super(Classifier1, self).__init__()self.l1 = nn.Linear(15, 15)self.l2 = nn.Linear(15, 15)self.l3 = nn.Linear(15, 1)self.relu = nn.ReLU(inplace=True)self.sigmoid = nn.Sigmoid()for m in self.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight)nn.init.constant_(m.bias, 0)def forward(self, x):x = self.relu(self.l1(x))x = self.relu(self.l2(x))x = self.sigmoid(self.l3(x))return xclass Classifier2(nn.Module):def __init__(self):super(Classifier2, self).__init__()self.l1 = nn.Linear(15, 15)self.l2 = nn.Linear(15, 15)self.l3 = nn.Linear(15, 1)self.relu = nn.ReLU(inplace=True)self.sigmoid = nn.Sigmoid()for m in self.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight)nn.init.constant_(m.bias, 0)def forward(self, x):x = self.relu(self.l1(x))x = self.relu(self.l2(x))x = self.sigmoid(self.l3(x))return xreturn Generator(), Classifier1(), Classifier2()def discrepancy_slice_wasserstein(p1, p2):s = p1.shapeif s[1]>1:proj = torch.randn(s[1], 128)proj *= torch.rsqrt(torch.sum(torch.mul(proj, proj), 0, keepdim=True)) #归一化处理p1 = torch.matmul(p1, proj)    #投影到新的空间中p2 = torch.matmul(p2, proj)p1 = torch.topk(p1, s[0], dim=0)[0]    #仅保留前s[0]个最大值。确保两个张量的形状一致。p2 = torch.topk(p2, s[0], dim=0)[0]dist = p1-p2wdist = torch.mean(torch.mul(dist, dist))return wdistdef discrepancy_mcd(out1, out2):return torch.mean(torch.abs(out1 - out2))def load_data():# Load inter twinning moons 2D dataset by F. Pedregosa et al. in JMLR 2011moon_data = np.load('moon_data.npz')x_s = moon_data['x_s']y_s = moon_data['y_s']x_t = moon_data['x_t']return torch.from_numpy(x_s).float(), torch.from_numpy(y_s).float(), torch.from_numpy(x_t).float()#网格点生成，返回 xx 和 yy 矩阵
def generate_grid_point():x_min, x_max = x_s[:, 0].min() - .5, x_s[:, 0].max() + 0.5y_min, y_max = x_s[:, 1].min() - .5, x_s[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))return xx, yyif __name__ == "__main__":parser = argparse.ArgumentParser()parser.add_argument('-mode', type=str, default="adapt_swd",choices=["source_only", "adapt_mcd", "adapt_swd"])parser.add_argument('-seed', type=int, default=1234)opts = parser.parse_args()# Load datax_s, y_s, x_t = load_data()# set random seedtorch.manual_seed(opts.seed)torch.backends.cudnn.enabled = Truetorch.backends.cudnn.deterministic = True# Network definitiongenerator, cls1, cls2 = toyNet()generator.train()cls1.train()cls2.train()# Cost functionsbce_loss = nn.BCELoss()# Setup optimizersoptim_g = torch.optim.SGD(generator.parameters(), lr=0.005)optim_f = torch.optim.SGD(list(cls1.parameters())+list(cls2.parameters()), lr=0.005)optim_g.zero_grad()optim_f.zero_grad()# # Generate grid points for visualizationxx, yy = generate_grid_point()# For creating GIF purposegif_images = []#在每个步骤中生成并保存图像 for step in range(10001):if step%1000==0:print("Iteration: %d / %d" % (step, 10000))z = torch.from_numpy(np.c_[xx.ravel(), yy.ravel()]).float()#将 xx 和 yy 矩阵展平并拼接起来with torch.no_grad():fea = generator(z)Z = (cls2(fea).cpu().numpy()>0.5).astype(np.float32)Z = Z.reshape(xx.shape)f = plt.figure()plt.contourf(xx, yy, Z, cmap=plt.cm.copper_r, alpha=0.9) #绘制对应的等高线图plt.scatter(x_s[:, 0], x_s[:, 1], c=y_s.reshape((len(x_s))), #绘制散点图cmap=plt.cm.coolwarm, alpha=0.8)plt.scatter(x_t[:, 0], x_t[:, 1], color='green', alpha=0.7)plt.text(1.6, -0.9, 'Iter: ' + str(step), fontsize=14, color='#FFD700',bbox=dict(facecolor='dimgray', alpha=0.7))plt.axis('off')f.savefig(opts.mode + '_pytorch_iter' + str(step) + ".png", bbox_inches='tight',pad_inches=0, dpi=100, transparent=True)gif_images.append(imageio.imread(opts.mode + '_pytorch_iter' + str(step) + ".png"))plt.close()optim_g.zero_grad()optim_f.zero_grad()fea = generator(x_s)pred1 = cls1(fea)pred2 = cls2(fea)loss_s = bce_loss(pred1, y_s) + bce_loss(pred2, y_s)loss_s.backward()optim_g.step()optim_f.step()if opts.mode == 'source_only':continueoptim_g.zero_grad()optim_f.zero_grad()loss = 0src_fea = generator(x_s)src_fea = src_fea.detach()src_pred1 = cls1(src_fea)src_pred2 = cls2(src_fea)loss += bce_loss(src_pred1, y_s) + bce_loss(src_pred2, y_s)# loss_s.backward()tgt_fea = generator(x_t)tgt_fea = tgt_fea.detach()tgt_pred1 = cls1(tgt_fea)tgt_pred2 = cls2(tgt_fea)if opts.mode == 'adapt_swd':loss_dis = 2*discrepancy_slice_wasserstein(tgt_pred1, tgt_pred2)else:loss_dis = discrepancy_mcd(tgt_pred1, tgt_pred2)loss -= loss_disloss.backward()optim_f.step()optim_g.zero_grad()tgt_fea = generator(x_t)tgt_pred1 = cls1(tgt_fea)tgt_pred2 = cls2(tgt_fea)if opts.mode == 'adapt_swd':loss_dis = discrepancy_slice_wasserstein(tgt_pred1, tgt_pred2)else:loss_dis = discrepancy_mcd(tgt_pred1, tgt_pred2)loss_dis.backward()optim_g.step()# Save GIFimageio.mimsave(opts.mode + '_pytorch.gif', gif_images, duration=0.8)print("[Finished]\n-> Please see the current folder for outputs.")