洛谷 P1033 自由落体

本文主要是介绍洛谷 P1033 自由落体，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

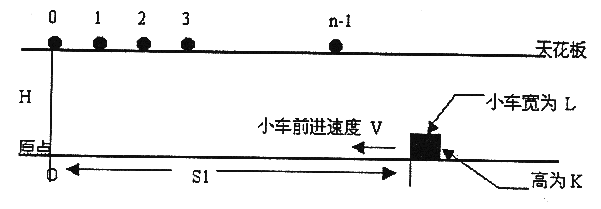
在高为 H 的天花板上有 n 个小球，体积不计，位置分别为 0，1，2，…．n-1。在地面上有一个小车（长为 L，高为 K，距原点距离为 S1）。已知小球下落距离计算公式为 d＝1/2*g*(t^2)，其中 g=10，t 为下落时间。地面上的小车以速度 V 前进。

如下图：

小车与所有小球同时开始运动，当小球距小车的距离 <= 0.0001(感谢Silver_N修正) 时，即认为小球被小车接受（小球落到地面后不能被接受）。

请你计算出小车能接受到多少个小球。

输入输出格式

输入格式：
键盘输人：

H，S1，V，L，K，n （l<=H，S1，V，L，K，n <=100000）

输出格式：
屏幕输出：

小车能接受到的小球个数。

输入输出样例

输入样例#1：
5.0 9.0 5.0 2.5 1.8 5
输出样例#1：
1

---

利用相对运动的观点，假设小车不动，则所有小球都以水平速度v向右做平抛运动。

---

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const double eps=1e-4;
int n,ans;
double h,s,v,l,k,g=10;
int main()
{scanf("%lf%lf%lf%lf%lf%d",&h,&s,&v,&l,&k,&n);for(int i=0;i<=n-1;i++)if(sqrt(2*h/g)*v>=s-i-eps&&sqrt(2*(h-k)/g)*v<=s-i+l+eps)ans++;printf("%d\n",ans);return 0;
}

这篇关于洛谷 P1033 自由落体的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---