【可解释性机器学习】排列重要性（Permutation Importance）及案例分析详解

当训练得到一个模型之后，除了对模型的预测感兴趣之外，我们往往还想知道模型中哪些特征更重要，哪些特征对对预测结果的影响最大。 Permutaion Importance，排列重要性，就是一种衡量特种重要性的方法。

引言

训练得到一个模型之后，我们可能会问的一个最基本的问题是：哪些特征对预测结果的影响最大？这一概念叫做特征重要性。

测量特征重要性的方法有多种。有些方法对上述问题的不同版本做出了微妙的回答。其他方法也存在documented shortcomings。

与其它方法相比，排列重要性具有以下优点：

• 计算速度快
• 应用广泛，易于理解
• 与我们期望一个特征重要性度量所具有的性质一致

工作原理

排列重要性使用模型的方式与你迄今为止所见到过的都不同，而且在一开始，很多人都会对其感到很困惑。所以首先举一个例子来具体介绍以下它。

假定有以下格式的数据集：

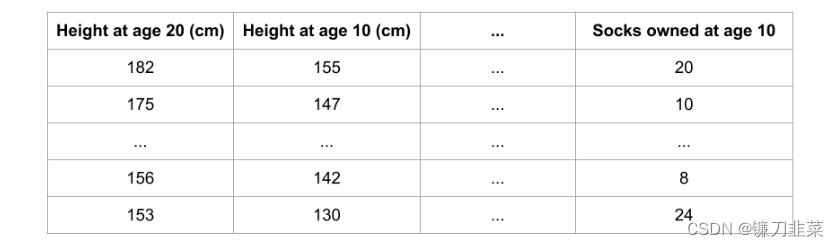
我们想用一个人10岁的数据去预测他20岁的身高是多少？
数据中包含：

• 有用的特征（10岁时的身高）
• 较弱的特征（10岁时拥有的股票）
• 对预测基本没有作用的特征

排列重要性是要在模型拟合之后才能进行计算。 所以对于给定的身高、股票数量等取值之后，计算排列重要性并不会改变模型或者是它的预测结果。相反，我们会问以下问题：如果随机打乱验证数据某一列的值，保持目标列以及其它列的数据不变，那么这种操作会在这些打乱的数据上对预测准确率产生怎样的影响？

**对某一列进行随机排序应当会降低预测的准确率，这是因为产生的数据不再对应于现实世界中的任何东西。如果随机打乱的那一列模型预测对其依赖程度很高，那么模型准确率的衰减程度就会更大。**在这个例子中，打乱height at age 10将会让预测结果非常差。但是如果我们随机打乱的是socks owned，那么产生的预测结果就不会衰减得那么厉害。

有了上述认识之后，排列重要性就按照以下步骤进行计算：

1. 得到一个训练好的模型
2. 打乱某一列数据的值，然后在得到的数据集上进行预测。用预测值和真实的目标值计算损失函数因为随机排序升高了多少。模型性能的衰减量代表了打乱顺序的那一列的重要程度。
3. 将打乱的那一列复原，在下一列数据上重复第2步操作，直到计算出了每一列的重要性。

代码示例

下面的例子会用到这样一个模型，这个模型用球队的统计数据预测一个足球队会不会出现“全场最佳球员”。“全场最佳球员”奖是颁发给比赛里表现最好的球员的。我们现在关注的并不是建模的过程，所以下面的代码只是载入了数据，然后构建了一个很基础的模型。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifierdata = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
my_model = RandomForestClassifier(n_estimators=100, random_state=0).fit(train_X, train_y)

数据预览:

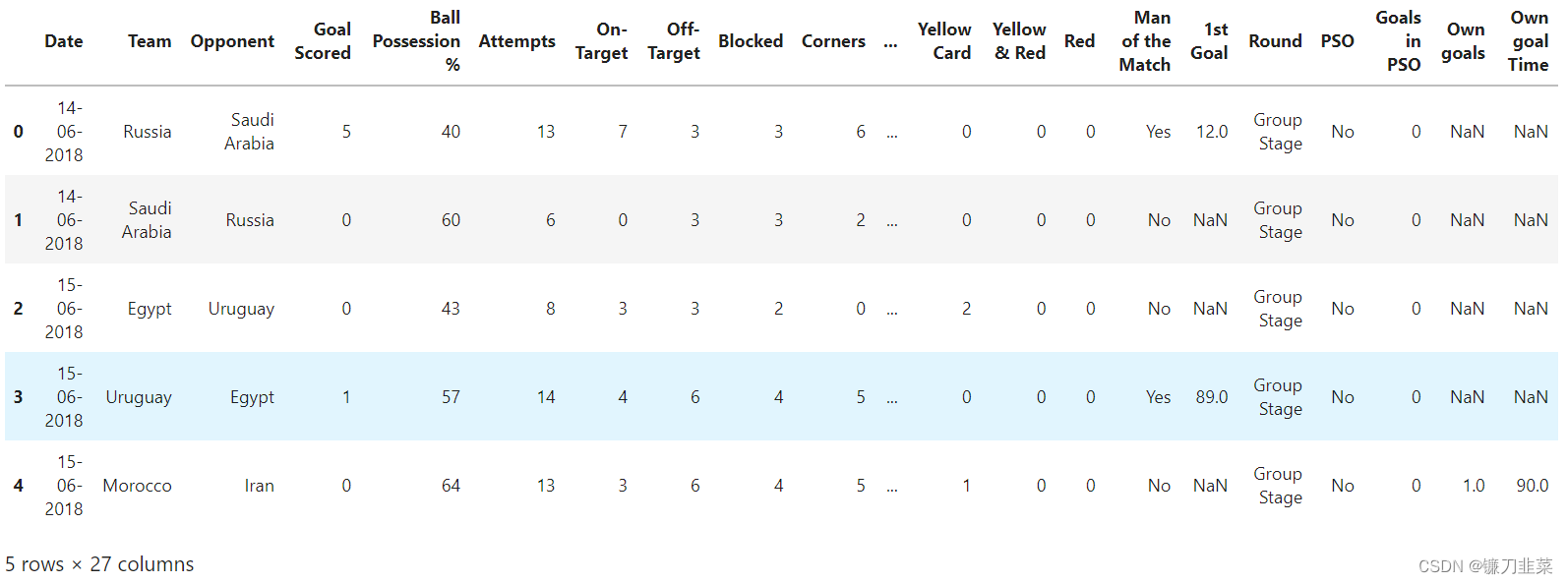
下面演示如何用eli5库计算和展示排列重要性。

import eli5
from eli5.sklearn import PermutationImportanceperm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())

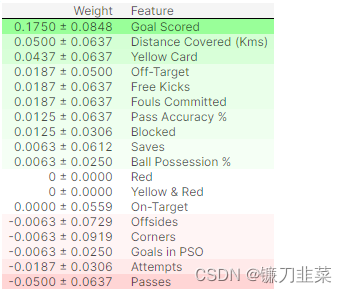
排列重要性结果解读

• 排在最上面的是最重要的特征，排在最下面是重要性最低的特征。
• 每一行的第一个数字表示模型性能衰减了多少（在这个例子中，使用准确率作为性能度量）。
• 跟数据科学里面的很多事情一样，在对某一打乱的特征提取重要性的时候，是存在随机性的，所以我们在计算排列重要性的时候，会通过多次打乱顺序的方式重复这一过程。在±后面的数字表示标准差。
• 偶尔会看到排列重要性的负值。在这些情况下，对混合(或嘈杂)数据的预测恰好比实际数据更准确。这种情况发生在特性并不重要的时候(重要性应该接近于0) ，但是随机的机会使得对混乱数据的预测更加准确。这在小型数据集(如本例中的数据集)中更为常见，因为存在更多的运气/机会空间。
• 在我们的示例中，最重要的特性是进球得分(Goals scored)。这似乎是明智的。对于其他变量的排序是否出人意料，球迷们可能有一些直觉。

模型检验

对于sklearn兼容的估计器eli5提供了PermutationImport包装器。如果想将此方法用于其他估计器，可以将它们包装在与 sklearn 兼容的对象中，或者使用eli5.permutation _ important模块，该模块具有基本的构造块。

例如，可以通过下面的方法检查skLearn.svm.SVC分类器的特性重要性，当使用非线性内核时，eli5不直接支持该分类器:

import eli5
from eli5.sklearn import PermutationImportance
from sklearn.svm import SVC# ... load datasvc = SVC().fit(X_train, y_train)
perm = PermutationImportance(svc).fit(X_test, y_test)
eli5.show_weights(perm)

如果没有单独的保留数据集，可以将PermutationImport安装在用于训练的相同数据上; 这仍然允许检查模型，但是不显示哪些特性对于泛化是重要的。
对于非sklearn模型，可以使用eli5.permutation_ important. get _ score _ important () :

import numpy as np
from eli5.permutation_importance import get_score_importances# ... load data, define score function
def score(X, y):y_pred = predict(X)return accuracy(y, y_pred)base_score, score_decreases = get_score_importances(score, X, y)
feature_importances = np.mean(score_decreases, axis=0)

特征选择

这种方法不仅适用于introspection，也适用于特征选择——人们可以使用排列重要性计算特征重要性，然后使用sklearn的SelectFromModel 或RFE去掉不重要的特征。在这种情况下，传递给PermutationImport的估计器不一定fit; 特性重要性可以针对多个 train/test 拆分计算，然后取平均值：

import eli5
from eli5.sklearn import PermutationImportance
from sklearn.svm import SVC
from sklearn.feature_selection import SelectFromModel# ... load dataperm = PermutationImportance(SVC(), cv=5)
perm.fit(X, y)# perm.feature_importances_ attribute is now available, it can be used
# for feature selection - let's e.g. select features which increase
# accuracy by at least 0.05:
sel = SelectFromModel(perm, threshold=0.05, prefit=True)
X_trans = sel.transform(X)# It is possible to combine SelectFromModel and
# PermutationImportance directly, without fitting
# PermutationImportance first:
sel = SelectFromModel(PermutationImportance(SVC(), cv=5),threshold=0.05,
).fit(X, y)
X_trans = sel.transform(X)

请注意，排列重要性应该谨慎地用于特征选择(像许多其他特征重要性度量)。例如，如果几个特征是相关的，并且估计器平等地使用它们，那么对于所有这些特征，置换重要性可能会很低: 放弃一个特征可能不会影响结果，因为估计器仍然可以从其他特征获得相同的信息。因此，如果基于重要性阈值删除特征，那么这些相关特征可以同时删除，而不管它们是否有用。RFE 和类似的方法(相对于单阶段特征选择)可以在一定程度上帮助解决这个问题。

补充分析

下图是随即森林模型和决策树模型的特征重要性结果：

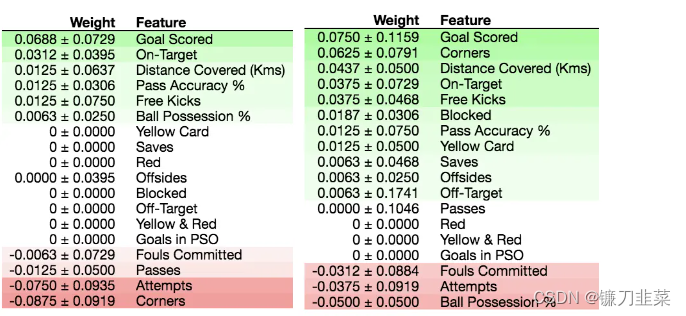
可以看到对于最总要的特征，两个模型的意见是一致的，那就是进球数（Goals scored），然而对于第二重要的特征，随机森林认为射中目标最为重要，然而决策树认为，发更多的角球才是王道，坚决放弃控球，虽然随即森林认为发角球鸟用都没有，是最不重要的。

Partial Dependency Plot

在了解了特征重要性后，我们还想了解每一个特征具体是如果影响模型决策的，这个时候就可以利用PDP或者ICE来进一步分析。PDP的基本思路就是控制其它所有特征不变，改变要分析的特征，看看它对预测结果的影响。ICE和PDP类似，ICE会显示所有实例上的分析结果。

（1）首先分析进球数对预测的影响

from matplotlib import pyplot as plt
from pdpbox import pdp, get_dataset, info_plots
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=my_model_1, dataset=val_X, model_features=feature_names, feature='Goal Scored')
pdp.pdp_plot(pdp_goals, 'Goal Scored', plot_pts_dist=True)
plt.show()

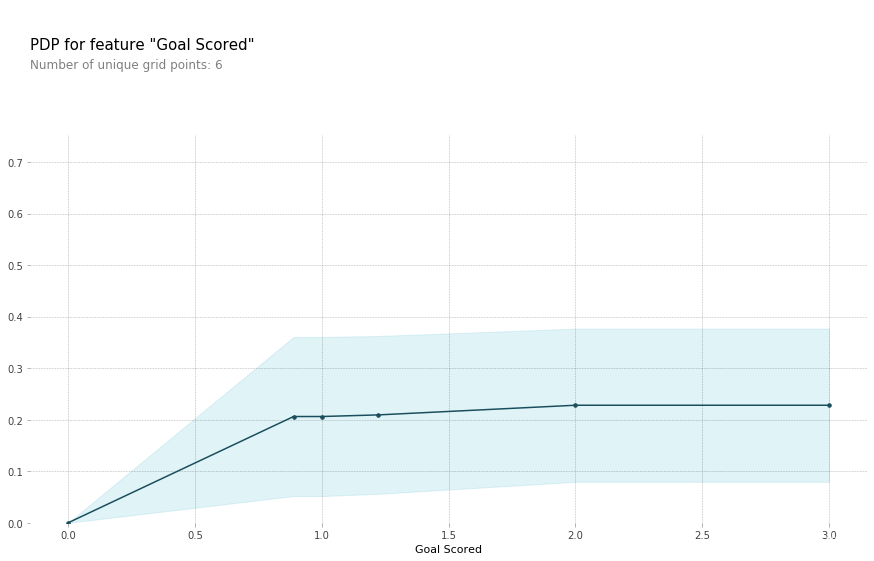
从PDP图中可以看出从不进球到近一个球，对预测的结果又一个明显的上升的影响趋势。然而进一个球之后，进太多的球对预测结果影响很低。
（2）然后分析跑动距离对预测结果的影响。

feature_to_plot = 'Distance Covered (Kms)'
pdp_dist = pdp.pdp_isolate(model=my_model_1, dataset=val_X, model_features=feature_names, feature=feature_to_plot)pdp.pdp_plot(pdp_dist, feature_to_plot, plot_pts_dist=True)
plt.show()

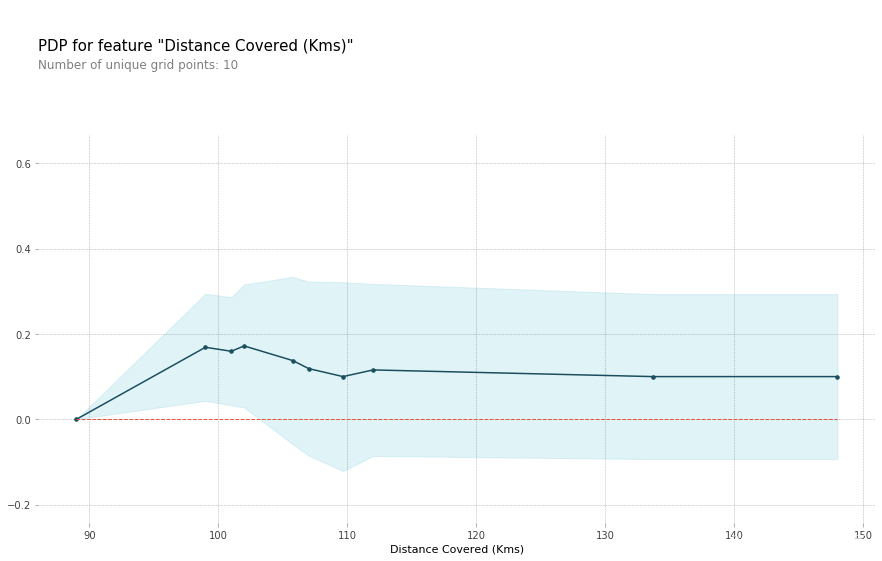
可以看出，当全队的跑动距离在100KM的时候，获得最佳球员的概率最大，然而跑动更多，概率反而下降了。

Sklearn也提供了PDP的支持：

import matplotlib.pyplot as plt
from sklearn.inspection import plot_partial_dependence
plot_partial_dependence(my_model_1, train_X, ['Goal Scored','Ball Possession %', 'Distance Covered (Kms)' , 'Corners', (0,1)], feature_names, grid_resolution=50) 
fig = plt.gcf()
fig.set_figheight(10)
fig.set_figwidth(10)fig.suptitle('Partial dependence')
plt.subplots_adjust(top=0.9, bottom = 0.1, wspace = 0.8)  # tight_layout causes overlap with suptitle

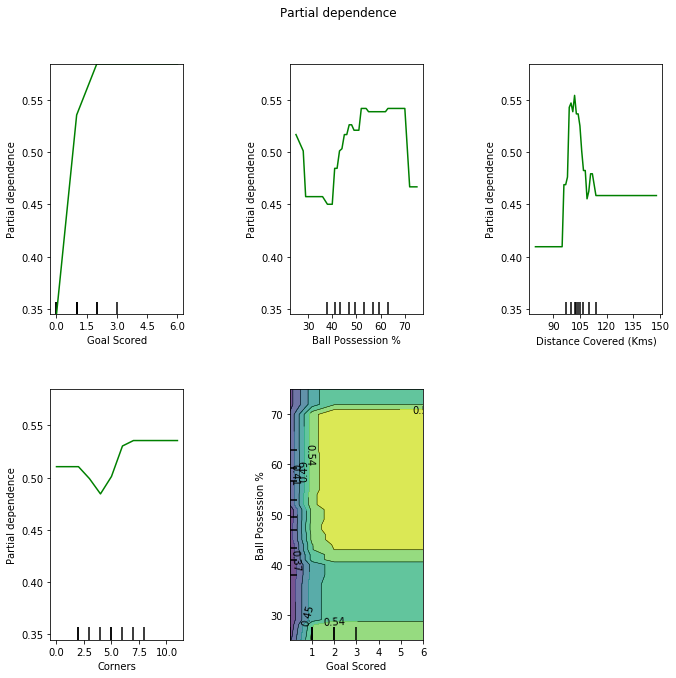
PDP最多可以分析两个特征。上图中的最后一个PDP图就是包含了对进球数和控球两个特征的分析。

Sharpley Value

PDP一般只针对某一个特征进行分析，最多两个，我们可以看出当分析两个特征的时候，PDP图已经不是一目了然的清楚了。Sharpley Value可以针对某一个数据实例，对所有的特征对预测的贡献作出分析。

首先，选取某一个训练数据，假定为第五个训练数据。该数据的具体内容如下：

row_to_show = 5
data_for_prediction = val_X.iloc[row_to_show]  # use 1 row of data here. Could use multiple rows if desired
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)
data_for_prediction
'''
Goal Scored                 2
Ball Possession %          38
Attempts                   13
On-Target                   7
Off-Target                  4
Blocked                     2
Corners                     6
Offsides                    1
Free Kicks                 18
Saves                       1
Pass Accuracy %            69
Passes                    399
Distance Covered (Kms)    148
Fouls Committed            25
Yellow Card                 1
Yellow & Red                0
Red                         0
Goals in PSO                3
Name: 118, dtype: int64
'''

pred_1 = my_model_1.predict_proba(data_for_prediction_array)
pred_2 = my_model_2.predict_proba(data_for_prediction_array)
pred_1,pred_2 
# (array([[0.3, 0.7]]), array([[0., 1.]]))

从预测上看，随机森林模型和决策树模型都认为该比赛本队获得最佳球员的可能性很大，其中决策树模型更是给出了100%的预测概率。那么我们就来看看利用Sharpley Value，每一个特征的具体贡献。

import shap  # package used to calculate Shap values# Create object that can calculate shap values
explainer = shap.TreeExplainer(my_model_2)# Calculate Shap values
shap_values = explainer.shap_values(data_for_prediction)
shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)

利用TreeExplainer可以分析决策树模型中，对该条数据的解释。红色部分表示正面的影响，蓝色是负面影响，Base Value 0.5是基准值，进球，射门数，犯规，角球和控球率等都提供了正分数，进球影响最大。而控球率等其它指标则提供了负分。总共一起，贡献了最终的输出值1。

KernelExplainer可以针对一般的模型进行Sharpley Value的分析，但是运算要慢一些。

k_explainer = shap.KernelExplainer(my_model_1.predict_proba, train_X)
k_shap_values = k_explainer.shap_values(data_for_prediction)
shap.initjs()
shap.force_plot(k_explainer.expected_value[1], k_shap_values[1], data_for_prediction)

上图是利用KernelExplainer，针对同一场比赛，对于随即森林模型的解释。

Summary Plot给出了所有数据点的分析汇总:

# Make plot. Index of [1] is explained in text below.
shap_values = k_explainer.shap_values(val_X)
shap.initjs()
shap.summary_plot(shap_values[1], val_X)

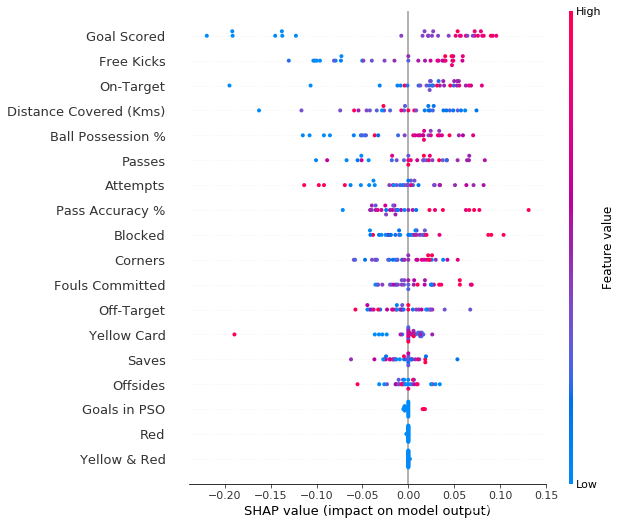
横坐标表示改值对于预测是正面的还是负面的，颜色标志了该值的大小。对于进球，我们发现，当进球数高的时候（红色），多为正面影响，而进球数低的时候，多为负面影响。有意思的黄牌数，大部分情况无论颜色，所有的点都集中在中间，也就是说得多少黄牌对于是否能评选本场最佳影响不大，然而有一场比赛，有一个特例，高的黄牌数对是否获得本场最佳产生了很大的负面影响。

还可以利用shap.dependence_plot来分析两个特征之间的相互影响:

explainer = shap.TreeExplainer(my_model_1)
# Calculate Shap values
shap_values = explainer.shap_values(X)
# make plot.
shap.dependence_plot('Ball Possession %', shap_values[1], X, interaction_index="Goal Scored")

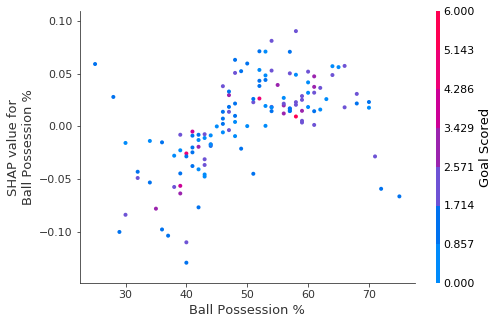
上图是控球和进球数两个指标对Sharpley Value的影响。同样的，当出现位置，颜色两个可视化属性来提供分析的时候，我们人类是很难很好的读出图中的含义的。我们把焦点放在右下角的两个点。这两个点是所有比赛中控球率最高的两场比赛，但是右边这个点的Sharpley Value更低，从这个角度来看更多的控球对于本队获得最佳球员，更为不利。

LIME

LIME 全称是local interpretable model-agnostic explanations直译是局部可解释的模型无关的解释，非常拗口。LIME针对某个实例，假定在局部，模型是简单的线性模型，对该数据点作出解释，是一种解释黑盒估计量预测的算法。

1. 根据我们将要解释的例子生成一个假的数据集。
2. 使用黑盒估计器为生成的数据集中的每个示例获取目标值(例如，类概率)。
3. 训练一个新的白盒估计器，使用生成的数据集和生成的标签作为训练数据。这意味着我们正在尝试创建一个估计器，它的工作原理与黑盒估计器相同，但是更容易检查。它不必在全局范围内工作得很好，但是它必须在接近原始示例的区域内很好地近似黑盒模型。
   要表示“接近原始示例的区域”，用户必须为生成的数据集中的示例提供距离/相似度度量。然后根据训练数据与原始样本之间的距离进行加权——样本越远，训练数据对白盒估计器权值的影响越小。
4. 通过这个白盒估计器的权重来解释原来的例子。
5. 白盒分类器的预测质量显示了它对黑盒分类器的近似程度。如果质量低，那么解释就不可信。

类似的，随机从训练集中取出一个点，用LIME来进行解释。该场比赛的数据如下：

import lime
import lime.lime_tabular
explainer = lime.lime_tabular.LimeTabularExplainer(train_X, feature_names=feature_names, class_names=['No','Yes'], discretize_continuous=False)
train_sample = train_X.sample(n=1)
train_sample

分别使用随机森林模型和决策树模型进行预测：

pred_p_1 = my_model_1.predict_proba(train_sample.values)
pred_p_2 = my_model_2.predict_proba(train_sample.values)
pred_1 = my_model_1.predict(train_sample.values)
pred_2 = my_model_2.predict(train_sample.values)
pred_p_1,pred_1,pred_p_2,pred_2
'''
(array([[0.1, 0.9]]),array(['Yes'], dtype=object),array([[0., 1.]]),array(['Yes'], dtype=object))
'''

利用LIME，可以给出LIME对于决策树模型下，给场比赛的解释。

exp = explainer.explain_instance(train_sample.values[0], my_model_2.predict_proba, num_features=len(feature_names),  top_labels=1)
exp.show_in_notebook(show_table=True, show_all=False)

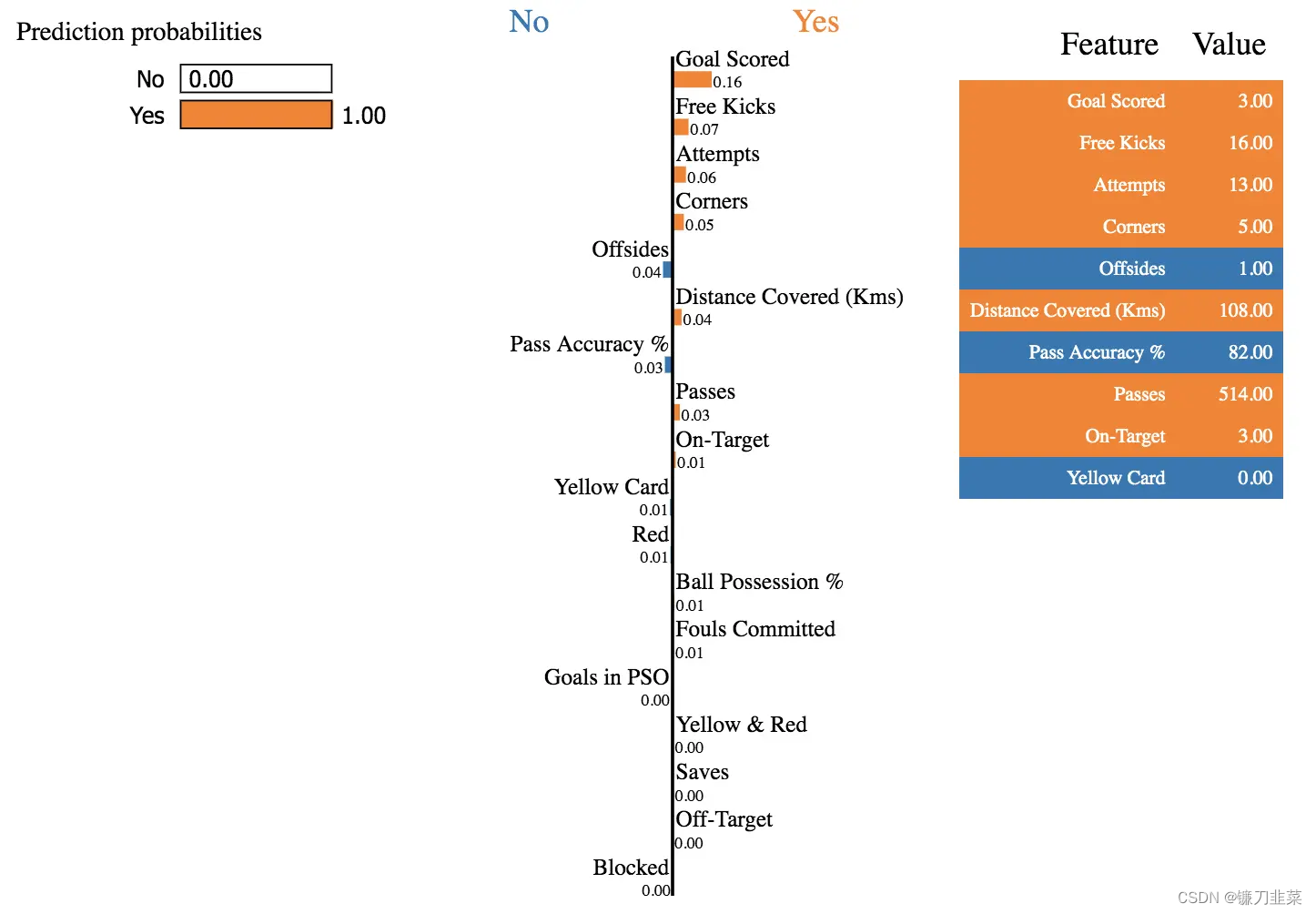
比起本文中的表数据，LIME跟擅长对于文本数据和深度神经网络进行解释。

总结

本文利用俄罗斯世界杯数据，构建了两个模型（随机森林模型和决策树模型）来预测本场最佳球员，并利用Permutation Importance/PDP/Sharpley Value/LIME等工具来对这两个模型进行解释，并给出一些如何解释机器学习模型的实际操作的例子。可以看出，虽然有诸多的工具，但是对于模型的解释还是需要利用对足球的理解和知识来阐述的，也就是说所有提供解释不可避免的需要领域专家的介入。

参考资料

[1] Permutation Importance
[2] Permutaion Importance —— 排列重要性
[3] 机器学习模型可解释性实战-预测世界杯当场最佳
[4] Permutation Importance
[5] LIME