AI研习丨专题：融合计量经济学思想的可解释深度学习

2021-03-11 18:02:31

摘 要

深度学习的可解释性问题严重制约其在社会科学、医疗健康等一些关键领域的应用。计量经济学作为一门非常重视解释的学科，其看待回归模型的视角为解决深度学习解释性问题提供了思路。本文将计量经济学中的自变量对因变量影响分析引入到了深度学习中，提出了基于敏感性分析的深度学习解释框架，并提供了交通拥堵分析、医疗诊断解释和金融投资策略三个应用案例。该框架能为深度学习可解释性问题提供来了新的研究思路。

关 键 字

深度学习；可解释性；计量经济学；敏感性分析

0 引言

过去的十几年中，深度学习技术蓬勃发展。深度学习基于深层的神经网络模型，其灵活的网络结构非常适合描述现实世界中复杂多变的非线性关系。深度学习技术的出现极大地提升了传统浅层模型的预测性能，并逐步在图像处理、文本分析和语音识别等应用中成为主流。然而，随着深度学习技术向医疗、社会、经济和管理等领域的渗透，其在解释性方面的一些缺陷也逐渐暴露出来。由于深度学习的模型结构过于复杂，人们无法直观理解其给出结果的过程和依据，基于深度学习的预测模型成为了一个不可解释的“黑盒”模型，造成了深度学习模型的解释性问题。

计量经济学是结合经济理论与数理统计，并以实际经济数据作定量分析的经济学分支。计量经济学与机器学习具有几乎相同的统计学基础，但由于解决问题的视角不同，两者在模型解释性问题的处理上截然不同。在计量经济学中，会使用回归模型来建模样本数据中变量之间的关系，并通过分析模型中因变量（输出变量）y 对于自变量（输入变量）x 的敏感性来衡量自变量对于因变量的影响。同样是回归模型，机器学习的视角会更加关注输出变量 y 预测的准确性，而计量经济学视角通过分析 x 对于 y 的影响来实现模型的解释。本文从计量经济学的视角重新审视深度学习模型，构建融合了计量经济学思想的深度学习模型解释框架，并通过交通预测、医疗诊断和量化投资中的三项具体应用案例展示解释框架的效力。

1 计量经济学中的模型解释

在统计学中，回归分析指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。最基本的回归模型是线性回归，其将因变量（y）表达为一个或多个自变量（x）的线性组合加一个与 x 无关的误差 ε。即 y=w0+w1 x1+…+wi xi+ε (1)作为一种基础性的经典模型，线性回归在机器学习和计量经济学领域都有非常广泛的应用，但是两个领域对于该模型的应用视角有着非常大的差别。

除了对于模型构成要素的关注点不同之外，在对于数据集的使用方面，机器学习和计量回归分析之间也有着非常大的区别。在机器学习模型中，数据集通常会被分为训练集、验证集和测试集三个部分。其中，训练集用来训练模型参数；验证集用来选择模型超参数；测试集用于评价模型的预测性能。这样的数据集划分的目的是为了服务于模型的预测应用。而在回归分析方法中，所有的数据都会被用于求解模型参数，数据集内的分析被称为“样本内”分析；用于预测的部分称之为“样本外”分析。样本内分析的主要目的在于揭示数据样本中存在的实证数据关系，而不单纯是为了进行参数的选择。

可以看出，根据视角的不同，不同学科领域对于相同数据和模型的使用方法也非常不同。机器学习方法侧重于模型的预测性能，而计量经济学方法更加关注模型对于数据中因果关系的解释。这也给了我们一些启发，在深度学习模型应用日益广泛的今天，可以从计量经济学的角度去重新审视深度学习模型，来解决深度学习在解释性方面存在的问题。

2 计量经济学视角的深度学习模型解释

如图 1 所示，在深度学习模型中，线性回归用于度量 xi 与 y 之间关系的 wi 无法直接获得，因此需要构建新的变量来度量自变量对于因变量的影响。

Networks 已经能对含有一个隐藏层神经网络进行上述的假设检验。给定数据集和深度神经网络，如果能拒绝零假设，那么就确定 xi 对于 y 产生了实质性的非线性影响。进一步地，Ri 的大小就可以解释因变量对于自变量的影响强度的大小。与此同时，使用由样本内数据训练获得神经网络，可以实现对于样本外数据的高性能预测。深度学习的解释能力和预测能力得到了有机统一，实现了真正意义上的深度可解释预测。

3 深度学习敏感性分析解释的应用案例

上文提出的基于敏感性分析的深度学习模型解释框架，可以被应用在许多真实世界的应用场景中，使得深度学习在提供强大预测能力的同时，实现对于真实世界复杂过程的解释。本文使用交通拥堵溯源、自动医疗诊断解释和投资组合决策解释三个应用案例进行说明。

3.1 城市交通拥堵溯源

在使用敏感性分析方法进行深度解释方面，我们最早开展的工作是使用深度学习模型进行交通速度预测，并采用敏感性分析方法解释道路交通之间的影响关系，实现对城市道路交通的拥堵溯源。如图 2 所示，在研究工作中，将道路切分为路段，对于第 s 个路段的第 t 个时刻，我们获得一个瞬时的速度采样 vst。

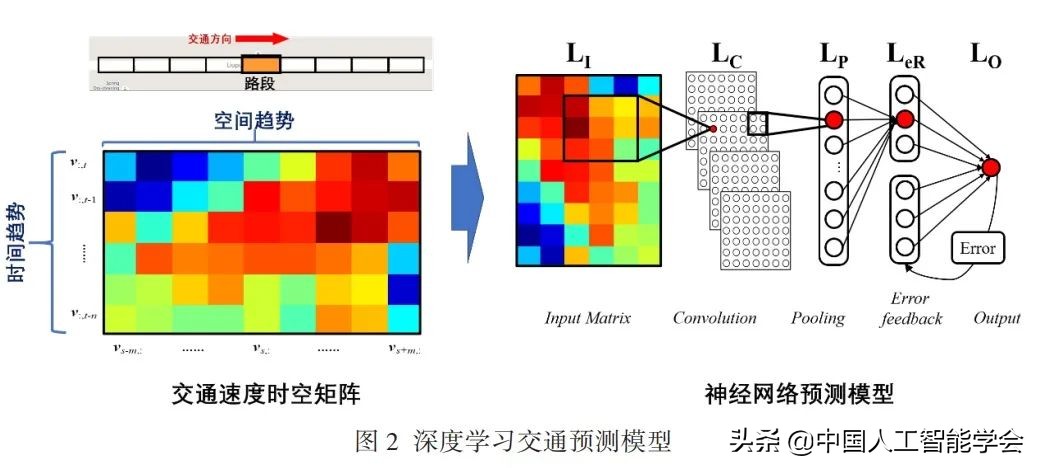
使用 vst 所构成的矩阵，就可以描述一条道路在时空两个方面的速度变化趋势。为了提取矩阵中的时空局部性特征，设计了一个卷积神经网络来对输入数据进行处理，最后通过一个 Error feedback 递归神经网络层来修正预测误差。该模型结构被称之为

Error-feedback Recurrent Convolutional

Neural Networks（eRCNN）是最早使用深度神经网络来建模道路交通时空上下文的研究，在道路速度预测方面取得了非常好的效果。

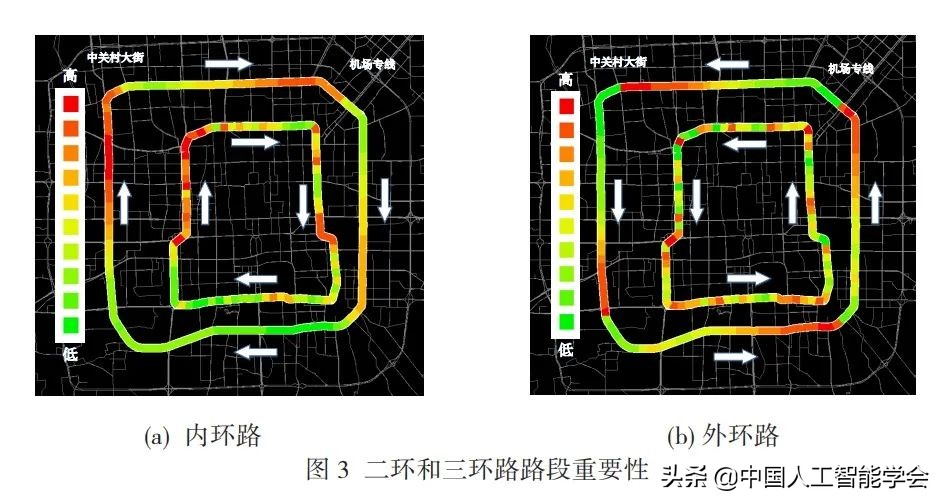
在整个路网中，Importancek 比较大的路段速度变化对于周边路段的速度变化影响较大，因此在整个路网中重要性较高。图3展示了二环和三环路各路段的重要性等级，红色表示高重要性路段。可以看出，高重要性的路段大多在环路的拐角，这是因为北京环路重要出入口多聚集在拐角附近，这些位置往往连接了其他重要道路。比如，两条环路的东北角连接通往首都机场高速路（东直门桥和三元桥）；三环路的西北角连接中关村大街；二环路的西北角连接北京北站。这些路段的拥堵往往会引发其他路段拥堵，是城市环路交通拥堵的源头。以上解释结果可以帮助城市规划者更好理解环路交通拥堵的成因，在城市计划和解决交通拥堵方面做出更好决策。

3.2 自动医疗诊断

敏感性分析方法不仅可以对深度神经网络输入和输出之间的关系进行分析，还可以分析网络的中间层输出对于最终输出的影响关系。我们可以从某一个中间层将网络一分为二，输入层到该中间层视为对输入数据的表征提取，中间层到输出层视为一个需要被解释的分类器。但通常情况下，网络中间层的输出是没有语义的，即便能对其进行解释，人类用户也难以理解模型表达的含义。因此，需要设计具有中间层语义的深度神经网络和敏感性解释器进行配合，实现深度神经网络的中间层解释。

这方面我们在研究工作中提出了一种将小波分解嵌入到深度神经网络中的模型结构，该模型主要用于时间序列的分类和预测任务。如图4所 示，在该模型中提出了一种 Multilevel Discrete Wavelet Decomposition (mWDN) 的神经网络。mWDN 能将输入的原始时间序列逐层地分解为高频和低频分量，整个过程等价于一个逐层的

Daubechies 小波分解，因此网络中间层的输出具有明确的语义——输入时间序列的不同频率分量。将 mWDN 模型和敏感性分析方法相结合，就能获得时间序列不同频率分量对于模型输出的影响。在 UCR Time Series Datasets 的时间序列分类实验中，mWDN 模型获得了非常好的分类效果，性能超过了全部的基线模型。

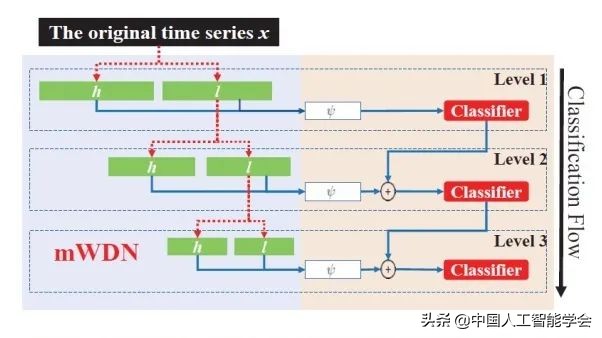
图 4 mWDN 小波时间序列分解模型

（图中，h 为高频分量；l 为低频分量）

图5给出了 mWDN 模型在心电图数据诊断方面的一个应用案例。如图所示，mWDN 网络首先将心电图的电压序列给分解成为不同的频率分量；然后再基于频率分量的结果给出检查者是否存在心脏疾病的判断。mWDN 模型除了能给出精准的预测判断之外，还能给出判断的依据。

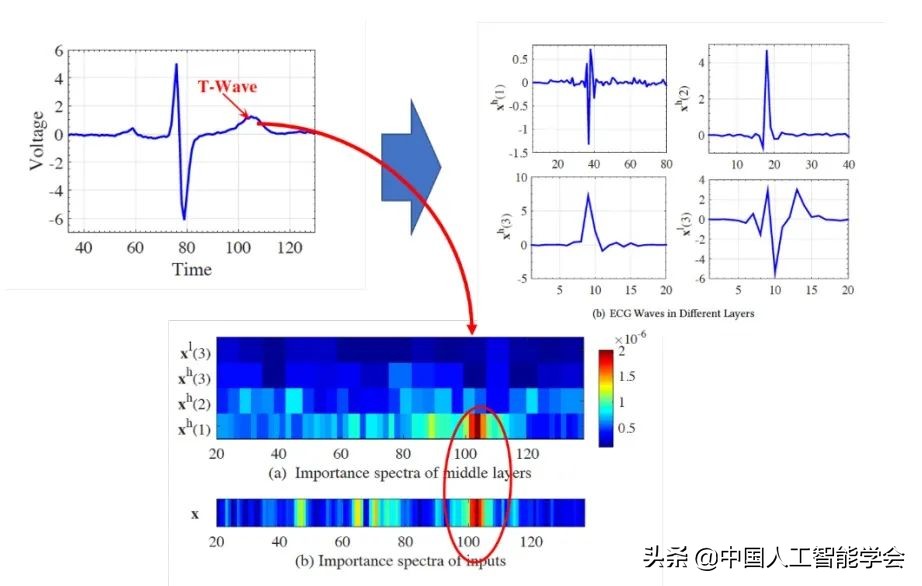
图 5 mWDN 心电图序列分类实（在光谱图中，xh 为高频分量；xl 为低频分量）

给定一个时间序列向量 x，将使用 mWDN 进行时间序列分类定义为

y=M(a(x))

其中，函数 M(.) 是 mWDN 神经网络；函数 a(.) 是 mWDN 在某一层的输出；y 是分类预测的输出。在 mWDN 中，a 是时间序列 x 的某个频率分量。那么，y 对于输入的某个频率分量的敏感性定义为

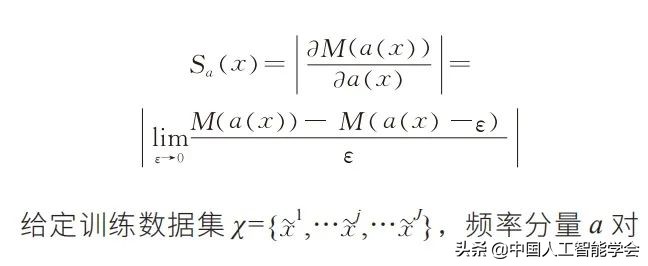
在引入敏感性分析之后，用户可以明确地知道深度学习模型给的出诊断结果基于了什么依据，这对于医疗诊断这种对解释性要求很高的场景来说非常重要。

3.3 金融市场投资

敏感性分析方法不但可以应用于有监督学习的预测问题中，同样也可以应用于深度强化学习中。有监督学习模型输入和输出之间的关系反映了客观数据中的物理关系，而强化学习的输出是一组决策行为，因此解释强化学习输入对输出影响的本质是为模型的决策结果寻找依据。

在研究工作中，我们提出了一种基于深度强化学习模型的股票市场投资组合生成模型，称 为 AlphaStock。如图6所示，该模型使用一个带历史注意力机制的 LSTM 模型（LSTM-HA）从股票特征时间序列数据中提取特征，并通过一个Transformer 模型生成股票的投资组合，也就是资金在各个股票上的投资分布情况。这里模型的输出并不是股票的价格等真实的监督值，而是如何进行投资资金分配的决策结果。

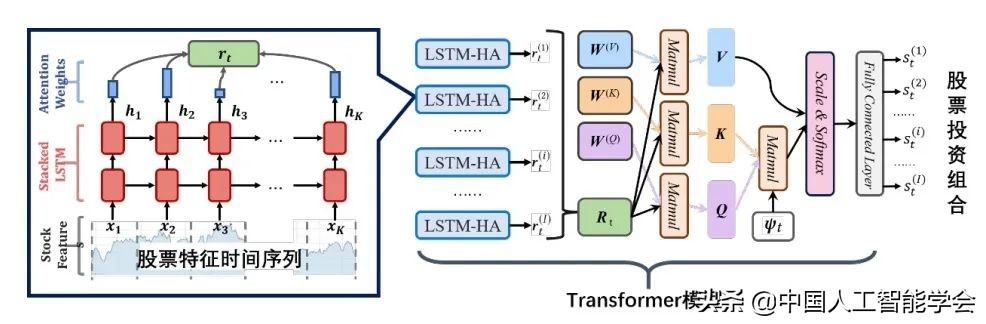
图 6 AlphaStock 强化学习投资组合生成模型

对 AlphaStock 模型进行解释的目的是为了给出模型进行资金分配的依据，这对于涉及大宗资金投入的金融投资来说至关重要。在 AlphaStock模型中，使用的股票时间序列特征包括股票价格涨幅、股票交易量、股票价格波动和公司特征等。敏感性的计算方法是令投资组合 s(i)=F(X) 表示股票 i 投资比例的生成函数，其中 X 表示股票的历史特征时间序列，是一个随时间变化的多维向量。使用敏感性分析方法分析 X 中的要素对于 s(i) 影 响，即可对 AlphaStock 的投资依据做出解释。在研究工作的实验中，算法对 1990—2018 年美国 NYSE、NYSE American、NASDAQ 和 NYSE Arca 四个交易所的全部股票进行回测交易，获得了 2.13 的夏普比率，最大回撤控制在 2.7% 内。

除了获得非常好的回测性能之外，AlphaStock模型还对投资股票的偏好进行了解释。图7示出了不同股票特征对于投资额的影响，图中特征对应的数值越大，说明模型越倾向于在具有该特征的股票上投入更多的资金。如图 (a) 和(b) 所示，股票远期（-12 个月）的价格涨幅和交易量具有较大的正向影响，而中近期（-6 个 月）的价格和涨幅具有较大的负向影响，这说明AlphaStock模型倾向于投资长期具有良好成长性，但短期内被低估的股票；如图 (c) 所示，股票历史价格的波动对于投资一直具有的负向影响，说明模型倾向于投资波动性较小的股票；如图 (d) 所示，市值 (MC)、市盈率 (PE) 和账面市值比 (BM) 均为正的影响，而股利 (DIV) 为负，这也反映了模型对于公司股票的一些投资偏好。对这些偏好的认识，可以帮助投资者理解模型交易的合理性，对于提高模型的鲁棒性，保障投资者的资金安全都有重要意义。

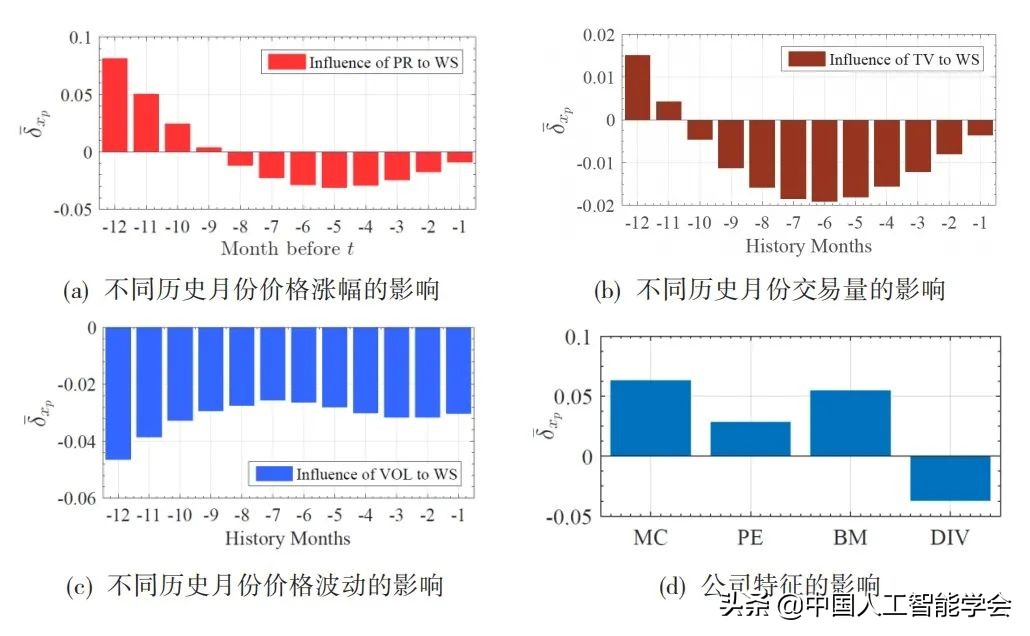
图 7 不同股票特征对于 AlphaStock 产生股票投资额的影响

9 结束语

本文从计量经济学的视角重新审视深度学习回归模型，通过将计量经济学中的模型解释引入到深度学习模型中，构建了基于敏感性分析的深度学习模型解释方法。通过交通预测、医疗诊断和金融投资三个案例的分析，可以看出敏感性分析方法在一些非常注重预测结果解释的场景中能发挥很大的作用。目前，计量经济学和机器学习的融合研究还非常初步，一些深层次的理论问题还没有解决，如复杂深度学习模型的显著性检验等，这也为两个领域的学者创造了巨大的研究机会。相信随着深度学习向医疗、金融、经济和管理等领域的不断渗透，计量经济学方法和机器学习方法会实现殊途同归，并最终形成坚实的理论体系，基于敏感性分析的深度学习模型解释也会在社会科学等领域实现广泛的应用，从根本上解决深度学习的解释问题。