【算法|动态规划No.15】leetcode1035. 不相交的线

本文主要是介绍【算法|动态规划No.15】leetcode1035. 不相交的线，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

个人主页：兜里有颗棉花糖
欢迎点赞👍 收藏✨ 留言✉ 加关注💓本文由兜里有颗棉花糖原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

点击直接跳转到该题目

1️⃣题目描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足以下两点：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。

示例 1：

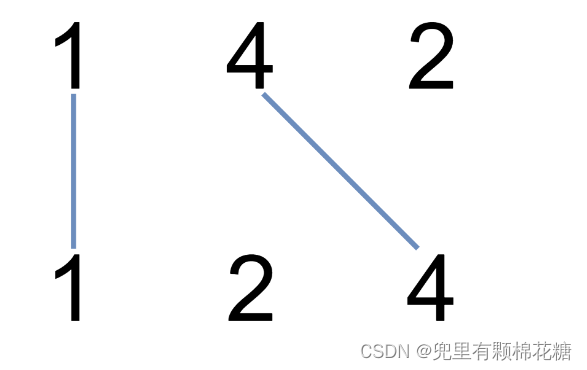
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

注意：

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

2️⃣题目解析

关于本题的思路，可以说基本上和leetcode1143. 最长公共子序列完全一样，简直就是一个题。可以参照我们上篇博客：leetcode1143. 最长公共子序列（点击直接跳转至该博客）

状态转移方程（这里我多开了一块空间，所以大家注意以下下标映射关系）：

if(nums1[i-1] == nums2[j-1]) 则dp[i][j] = dp[i - 1][j - 1] + 1
否则，dp[i][j] = max(dp[i-1][j],dp[i][j-1]);

返回值：

dp[m][n]

3️⃣解题代码

class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(),n = nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1;i <= m;i++){for(int j =1;j <= n;j++){if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};