线性代数基础2--消元求解,矩阵乘法与逆

1,消元法求解方程组
这里的消元过程其实就是矩阵阶梯化的过程,这就解释了为什么行列式只能进行行变换,因为它代表的含义是一个方程.
而系数矩阵就是方程组的简化形式.

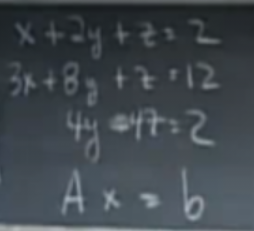
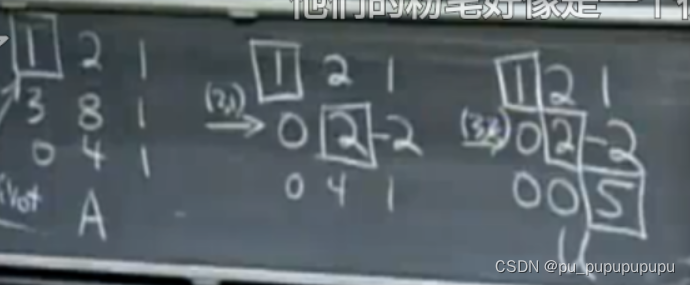
上图中,打方框的部分为主元,最终得到三个主元,主元不能为0,u表示上三角矩阵.
通过消元法,将A转化为上三角矩阵

消元法无法求解方程组的情况是,对于本例来说是无法得到三个主元.也即矩阵不可逆.

这时如果将矩阵加上结果行b.就成为了增广矩阵


最终将增广矩阵化简,然后回代(将矩阵重新写为方程组形式),得到上图的最终结果.即UX=C

2,线性代数核心概念
分别用行,列进行矩阵操作

在这里矩阵右乘一列,结果也为一列.这里用列进行操作,也可以看作向量进行操作.扩展x,表示多一列结果
而如果矩阵左乘一行,结果也为一行.这里表示进行行操作,这里如果x多一行,就表示结果多一行.
可以看成左乘做的是行操作.那么

这个操作用上面的思想来看,x的第一行(1,0,0)表示:结果的第一行就是矩阵的第一行,而第二行(-3,1,0)表示结果的第二行,为矩阵第二行减去矩阵第一行的三倍.
其中左边矩阵叫做初等矩阵,记为E

这里的E21表示在第二行与第一行之间进行变换.

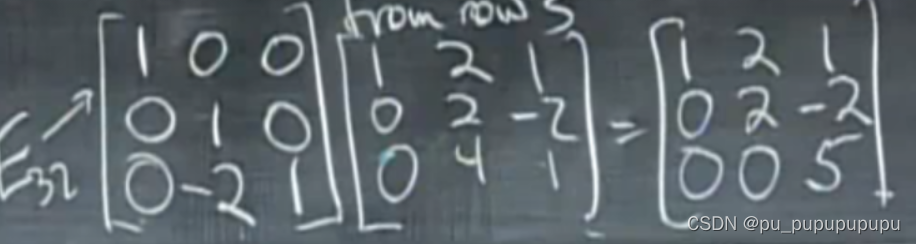
变换第二步如上.
注意不可以写成[[1,0,0],[-3,1,0],[0,-2,1]],因为第二行并不是变换后的第二行.

这里显示矩阵乘法满足结合率.可以将两个初等矩阵先相乘.
但是不满足交换律,即AB不等于BA

p矩阵称为置换矩阵,可以实现两行交换.

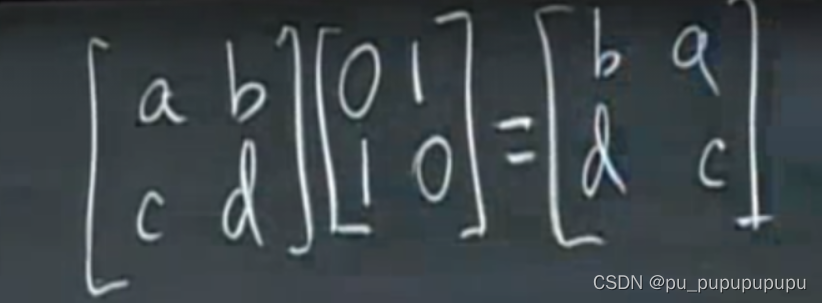
左行右列,如果进行列变换就要右乘.并且乘的时候也要看作列的形式.

3,逆

注意这里各个矩阵的记法.
逆矩阵简单来说,就是两个矩阵相乘得到一个单位矩阵.在这里就是逆矩阵取消了原初等变换.

4,矩阵乘法


C34就等于左3乘右4
这是基本的矩阵乘法.就像前面学习的左边的矩阵决定结果的行数,可以看成多一行,结果多一个方程.
右边矩阵决定结果列数,可以看成多一列,就多一个线性表示.这就引出矩阵乘法的另外理解方法.

矩阵乘法结果C的每一列都可以看作A中基(每一列为一个基)的一种线性组合,组合的系数为B的对应列.

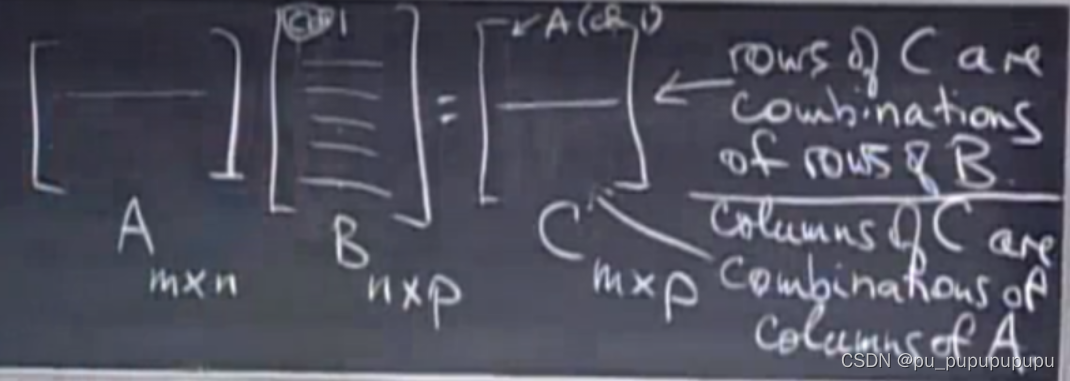
另一种看法按行来说,当然可以说,c中的一行,是b中行的线性组合,组合系数为a的一行.
当然,更直观的,是以方程形式解释,就如前一节的初等变换一样,A中一行可以看成B中行的组合.
第四种理解方式:第一种方法是行乘以列,那么这种方法就是列乘以行.


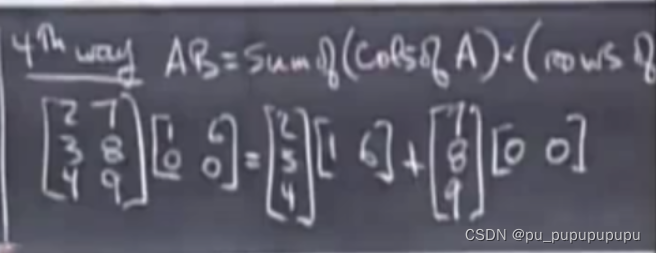
那么矩阵乘法就可以写成多个一列乘以一行,这有什么含义呢?
首先,一列乘以一行得到一个完整的矩阵,而其中每一个都可以看成一个基乘以一行,效果是基成倍变化,但结果向量始终在基这一条直线上.而每一个加号就代表叠加.

这里就有新的感觉,第一种方法与第三种方法为一组,结果都是相同的,取左边第一行,无论右边按行或列计算都得到第一个方程.
同样的,第二种与第四种方法为一组,第二种方法,是将A看成n列与B中一列,直接得到一个线性组合的结果,而第四种方法得到的是,所有线性组合中第一个基的分量.也就是说如果看成列来运算,B中的所有第一行的元素就对应第一个向量.

第五种方法:分块乘法

如图,第一位置得到的结果如上图.注意,这两个矩阵需要形状相同
那么这里可以有几种解释,
第一种,就按正常的一行与一列乘法,最后得到第一个位置.
第二种,按行来理解,结果想要得到第一行,那么需要A中第一行与B中所有行相乘,那么第一个位置就是A中第一行与B中所有行的第一个位置.
第三种,看成列来理解,要想得到目标向量,做法是b1**[a1,a3]+b3**[a2,a4],那么置得到第一个位置就是b1a1+b3a2.

5,逆

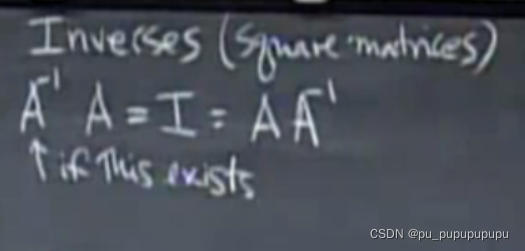
对于方阵来说,左逆与右逆相同,非方阵左右不同.

不可逆的情况,为什么不可逆.用向量来解释,需要得到单位矩阵,但是A中的两个向量是共线的,所以即使可能会得到(1,0)(0,1)向量中的一个,也绝不可能同时得到两个向量.

另一种,解释如果Ax=0,并且x不等于0,那么A就不可逆.因为如果A
可逆,等号两边同时乘以A逆那么,得到x=0,但是x不等于0.
那么如何理解Ax=0,AX=0就说明A中的几个基,至少有一个基是不产生作用的.按方阵来说,就不可能得到单位矩阵.

如何求A的逆

这里是最基础的方法.
把增广矩阵的左边化为单位矩阵,那么右边就可以得到A的逆.
为什么这样?因为EA=I,那么E就为A逆,根据分块矩阵的乘法,结果的后一个位置为EI那么就等于A逆了.