本文主要是介绍代数几何导引(德文版)【瑞士 马库斯·布罗德曼(Markus Brodmann)】的读书笔记,翻译和感想(3)-知识点的补充与拓展,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们上次在“代数几何导引(德文版)【瑞士 马库斯·布罗德曼(Markus Brodmann)】的读书笔记,翻译和感想(3)”中还有不少内容没有讲完,所以仅仅是作为知识点总结和拓展,我就不将标题的名称更改为“代数几何导引(德文版)【瑞士 马库斯·布罗德曼(Markus Brodmann)】的读书笔记,翻译和感想(4)”,只是简简单单将标题名称在第三讲的基础上添加一个一个“-知识点的补充和拓展”,可以和第三讲搭配阅读。
非常抱歉作者更新的速度较为慢,其主要原因就是要开学了,并且博主自己电脑的“d”键坏了,现在只能用学习提供的设备进行更新和研究,非常抱歉。
这是从上一讲的截图:
我想我们可以在这基础之上,添加或减少一些内容上的拓展以及概念上的应用,也许我们会用一些简单的例子或者题目来辅助我们的学习。
1.黎曼流形
①来自百度的概念
黎曼流形(Riemannian manifold)是一黎曼度量下的微分流形(关于微分流形,可以看上一讲的内容),设是
维光滑流形,若在
上给定一个光滑的二阶协变张量场
,则称呼
为一个
维流形,
称为该黎曼流形的基本张量或者黎曼张量,如果满足:
A)是对称的,即:
B)是正定的,即:
且等号仅在X=0的时候成立,
简单的来说,黎曼流形就是给定了一个光滑的对称的,正定的二阶张量场的光滑流形。
在微分流形以及黎曼几何中,一个黎曼流形是具有黎曼度量的微分流形,换句话说,这个流形上具有一个对成正定的二阶协变张量场,亦即在每一点的切空间配备一个正定二次型。
②一些来自中国的梅向明的《微分流形和黎曼几何》的常曲率黎曼流形
博主注:这里博主实际上并没有找到只关于“黎曼流形”的内容,我在这一本书中找到的实际上是关于“常曲率黎曼流形”,但实际上,在这一章节中很多讲的都是关于“常曲率黎曼流形”和“完备常曲率黎曼流形”,在这里博主就仅仅摘录一小段(常曲率黎曼流形)出来作为一些引申拓展,我在这里不抄录“完备常曲率黎曼流形”了
第十章 常曲率黎曼流形
常曲率黎曼流形
定义6 黎曼流形称为常曲率的,如果它的各点处所有平面截面的截面曲率等于相通的常数
,这时,局部地有
所以,曲率张量场是平行的,因此,这黎曼流形是局部对称的。
设是一个黎曼流形,
是
的一坐标域,局部坐标是
,
是
上的局部标准正交标架场,
是对偶标架场,则
上有结构方程
其中
如果M是长曲率的,注意现在
实例:
(1)维度欧式空间
;
(2)中的单位球面
,
;
(3)双曲空间,命
是
的上半平面
带有黎曼度量(注意
只用一个坐标域覆盖)
,即
命
这是
上的标准正交标架场,对偶标价场是
容易证明:
满足结构方程
2.度量空间
①来自苏联(С.С.C.Р.)的Д.В.Кангороеич和Г.П.Акилов的《泛函分析》(引用的是第二版,第一版书的中文翻译是《赋范空间中的泛函分析》)
 度量空间
度量空间
3.1. 度量空间是一类非常重要的拓扑空间,集合叫做度量空间,如果每一对元素
都对应一个实数
(元素
与
之间的距离),满足条件:
1)当且仅当
时
;
2)
3)对于任何,
(三角不等式)
所引进的函数叫做度量,
维度欧式几何空间
直线段,圆周(如果取点之间最短弧的长度作为圆周上的距离)等可以作为最简单的度量空间的例子
设是具有度量
的度量空间,集合
叫做以点为中心
为半径的开球
集合
叫做以点为中心的
为半径的闭球(下面通常简称为球)
定理1. 集合的总体满足2.3.中的条件1)-3),即构成集合
中的基底
证. 因为,所以条件1)显然成立,如果
且
,则
,于是,条件2)成立,如果
,则令
便有
,此外,如果
且
,则
,因为三角不等式,对于任何
,有
.由此可见,条件3)成立.
在定理2.1中挺进的构造,用典型的方式把度量空间变为以开球为基底的空间,定理1也指出,
中的每个点都具有可数的基底.所以,为了描述
中的拓扑,只须限于收敛序列(见2.6,性质6).我们指出,在所得拓扑空间中
当且仅当
.
其拓扑是由某种度量生成的拓扑空间叫做可度量化的(绝不是所有的拓扑空间都是可度量化的;这种空间的例子我们将在下面看到),应该指出,同一个拓扑可以由不同的度量生成.
定理2. 1) 是其变元的连续函数,即如果
,则
2)度量空间是Hausdorff空间(因而收敛序列只能有一个极限).
证. 1) 由三角形不等式得关系式
交换与
的位置,得到相反符号的不等式,由此
利用此式,得
2) 如果,则
,由三角形不等式推得,开球
和
不相交.
下面我们需要点到集合的距离的概念,如同在欧式空间一样,我们把这个量定义为
不难看出,等价于
设是度量空间
中的集合,因为对于集合
中德每一对元素都定义了距离,所以对于
中的元素对也定义了距离,显然,它满足度量空间的公理1)-3),从而
自然成为度量空间,这时我们就称在
中的度量是由空间
的度量诱导而得到的,或者称呼空间
是度量空间的
的子空间
假设在两个度量空间和
的元素之间可以建立一一对应,使得空间
和
对应的元素之间的距离相等,这样的空间叫做等距的,显然,在等距空间之一中具有的所有的度量关系,在另一个中也同样成立,因此,这样的空间之间的差别仅在于元素的具体性质,而不涉及与空间的距离有关的本质,这种情况为把等距的空间等同起来提供了根据.
博主注:
事实上,对于这句话“使得空间
和
对应的元素之间的距离相等”,我想必然有人要问如何计算度量空间之间的距离,不同的空间有不同的距离计算方法,所以有不同的度量空间,比如欧式空间,离散空间,可测函数和序列空间中的距离定义是不同的
3.2. 现在引进比较复杂的度量空间的例子,在本书中以函数作为元素的空间起着主要的作用,这里及以后,已经某个以数值函数为元素的空间时,如果没有相反的约定,我们总是同时考虑两个空间:由满足相应条件的实函数全体组成的实空间
以及由同样满足条件的复函数全体组成的复空间
,这两种空间在表示上照例是不加区分的,如果在某一个命题中,我们没有提到空间是实的或者复的,则表明这个命题在两种情况都成立.
1)设是紧空间,空间
是紧空间
上所有连续函数的集合,其中函数
和
之间的距离由下式定义:
验证条件1)-3)并不困难,因此我们忽略了,因为紧空间上的连续函数达到其最大值(见定理2.6),所以也可以写为
空间中元素序列
收敛于点
表示函数列
,一致收敛于函数
.事实上,如果按任意
选取
,使得当
的时候有
,则表示对这样的
从而对于所有的,不等式
成立,由此推得要证明的一致收敛性.
反之亦然:从连续函数一致收敛于连续函数推得在空间中对应元素的收敛性。如果
,则记为
.
2)空间是所有数列的集合,其中数列
与
之间的距离用以下的定义:
验证度量空间的公理1)与2)并没有困难,由于函数当
时递增,所以有数值不等式
从而推出条件3)成立.
如果序列收敛于元素
,则表示
即中点的序列的收敛是按坐标收敛,也就是点
的每个坐标都收敛于极限点
的对应的坐标.
事实上,由不等式
知,如果,则得
反之,如果条件(3)成立,由于级数
关于一致收敛(
是它的强级数),故可以逐项极限,且因级数的每一项都趋于0,所以
由上面的证明可以推导出,空间是可数的直线族的拓扑积.
我们还指出空间(为了和复空间
区分开来,这里我们对上指标加上圆括号),其元素是定义在
上且在此区间上有直到
阶连续导数的函数,
之间的距离可以定义为:
中的收敛表示函数序列以及
阶导数序列都一致收敛
我们也可以研究空间,它是由多维空间的区域
内自身以及直到
阶的偏导数都连续的函数所组成(见
)
我们指出,如果在中引进序:
当且仅当对于任何
有
而在
中约定,
当且仅当对于任何
有
,则
与
称为有序集(但不是全序的)
②来自百度的定义
度量空间也称为距离空间,一种拓扑空间,其上的拓扑由距离决定,设是一个非空集合,
是
上的二元函数,满足以下条件:
1.且
2.
3.
则称为两点
之间的距离,
按距离
成为度量空间或距离空间,记为
,设
是
的子集
3.度量
①来自百度的定义:
度量,也就是距离函数,是度量空间中满足特定条件的特殊函数,一般用来表示,度量空间也被称为距离空间,是一类特殊的拓朴空间。
详细定义:
设为一个非空集合,其元叫做点,
是全体实数的集。
若函数对于任意
满足条件;
(a),当且仅当
时候成立;(这个就是正定性)
(b);(对称性)
(c)(三角不等式)
则称呼函数为集合
上的一个距离函数或者度量,赋予度量
的集合
称为度量空间,记为
4.黎曼度量
①来自百度的定义
每个光滑流形都配有黎曼度量
定义一:
设为光滑流形,则
上的黎曼度量为
上光滑对称共变2张量场,且在
上每个点均为正定
定义二:
设为光滑流形,则
上的黎曼度量为
上每点
给定切空间
上的内积,且在
上各点光滑
②来自中国的伍鸿熙的《黎曼几何初步》的关于黎曼度量的内容
流形
上一个黎曼度量
是什么呢?我们帮助大家回忆一下定义,
是一个"
指定”。“指定”的含义就是对于
的每一个切向量空间
,指定
中的一个向量内积
(有时候
,记录为
,类似地有时记
为
)所谓指定的
的,那表示:对
的任意一个局部坐标系
,如今
则这些是坐标
的
函数,在此提醒注意:
是内积这一事实相当于矩阵
是正定对称的,如果用张量的语言来说,
其实就是
上一个
流形上总可以找到一个黎曼度量(参阅[CC],第130页定理1.1)
博主注:
1.勘误"(参阅[CC],第133页定理1.1)"为“(参阅[CC],第130页定理1.1)”,这里参阅的书籍是陈省身的《微分几何讲义》
参见的陈省身的《微分几何讲义》部分
定理1.1 在
维光滑流形
上必有黎曼度量
证明 取
的局部有限的坐标覆盖
,设
是从属的单位分解,使得支集
.命


其中
定义为

它们是
上的光滑的二次微分式.因为在每一点
式右端只是有限项的和,所以该式是有意义的,实际上,若取
的一个坐标域
使得
是紧致的,由于
的局部有限性,所以
只与其中有限多个成员
相交,因此
式限制在
上成为
其中

因为
,故有某一指标
,使
于是
由此可见,
在
上处处是正定的.
注记 在流形上黎曼度量的存在性并非平凡的结果,例如,
上不一定存在非正定的黎曼度量(但这一点较难证明),从纤维丛的观点看,在
上存在黎曼度量,说明
上对称的二阶协变张良从必有正定的光滑截面,然而,对于任意的矢量丛,处处不为零的光滑截面却不一定存在.
下面假定
是广义黎曼流形,在局部坐标系改变时,基本张量
的分量变换公式是

那么,容易证明
的坐标变换公式是

因此
是对称的二阶反变相量.
借助与基本张量,可以把切空间的余切空间等同起来,因而反变矢量和协变矢量可以看做是同一个矢量的不同表现形式,实际上,若
,命

则
是
上的线性函数,即
.反过来,因为
是非退化的,所以
中任意一个元素都可以表成
的形式,这样,对应
在
和
之间建立了同构,用分量表示,若
则从
式可以得到

此外,可以直接验证,如果
是反变矢量,则由
式定义的
遵从协变矢量的交换规律.
一般地,若
是
型张量,则

分别是
型张量和
型张量.如
式给出的运算通常称为张量指标的下降或上升.
连续统
①来自百度的定义
简单的来说,举个例子,我们说"实数集内实数可以连续变动",我们则称"实数集"为"连续统","平面是二维的连续统","空间是三维的连续统",更加严格的描述需要序理论和拓扑学的数学工具,连续统指的是"连续不断的数集"
一)连续统在数序中的定义
与区间对等的集合就叫做连续统,对等就是找到了一个映射,使得他们之间的元素满足一一映射
二)连续统在集合论中的定义与性质
在集合论中,连续统是一个拥有多于一个元素的线性序集,而且其序满足如下性质:
稠密:在任意两个元素之间存在第三个元素
无洞:由上界的非空子集一定有上确界,实数集即为连续统的例子,实际上它是连续统的原型
以下是连续统的例子:
序结构与实数集同构(序同构)的集合,例如在实数集和里面的任何开区间扩展实数轴,以及序同构域它的,比如单位区间。实的半开半闭区间如等,以及其序同构,拓扑学有一种比实数还要长的“长线”非标准分析中的超实数集。
切向量
①来自百度的定义
曲线在一点处的切向量可以理解为沿曲线该点处切线方向的向量.
切向量是与曲线相切的向量,给定曲线上一点
,
是
上与
的邻近一点,当
点沿曲线趋近于
时,割线
的极限位置称为曲线
在
的切线
导子
设为微分流形
中的一点,则
的切向量为
点的光滑函数芽
的导子
光滑曲线
光滑曲线在
点的切向量定义为
,则对
,
②来自美国的Martin M. Lipschutz的《Theory and problems of Differential Geometry》(纲要式丛书《Schaum's Outline Series》之一)
博主注:
这里博主采用参考的是于1989年9月出版的《微分几何的理论和习题》的中文翻译版本,由黄锦能,杨正清,李世杰先生翻译,左再思先生提出有益的建议,曾如皋好麦兆娴先生发现漏洞并作出改正
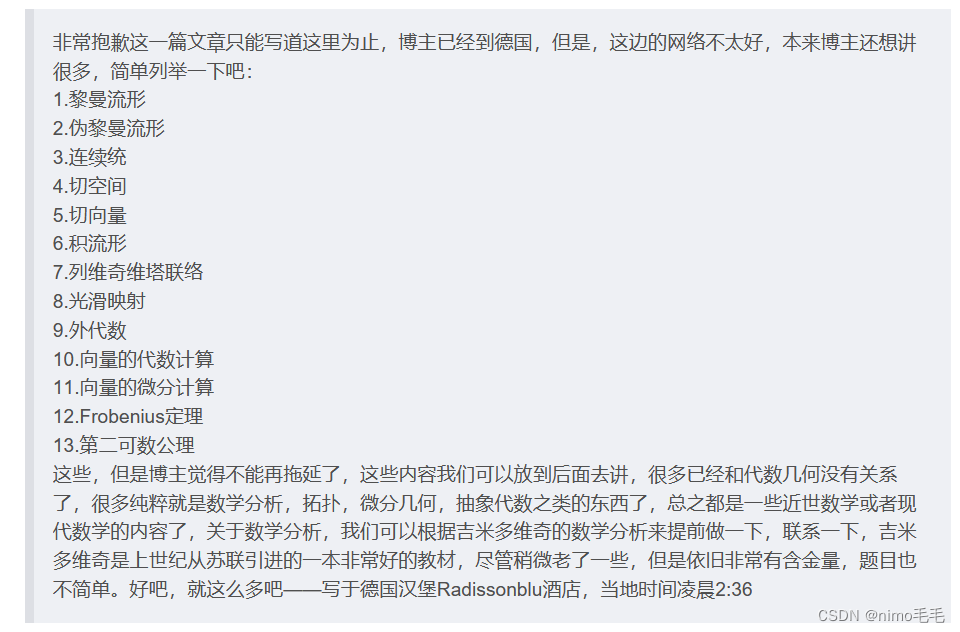
1.单 位 切 向 量
设是正则曲线
的自然参数表示,导数
用以确定
在点
的切线方向,这与我们的几何直觉相符,因为
且是
的割线方向,如图4-1所示,又因为对自然参数表示
,所以向量
还具有单位长度
若是
的另一个自然参数表示,则由定理3.4,
常数且
即与
有相同或者相反的方向,它取决于
的定向,于是
是定向的,在图4-1中,它的正向是s增加的方向
向量称为定向曲线
在
的单位切向量,并记作
例4.1 沿着螺线,
,有
且,于是
这里用到(定理3.4),我们看到,沿着这条螺线单位切向量
和
轴交成定角
如同单位切向量一样,沿着曲线的其他几何量也可用自然参数表示来确定,然而,像上面的例子,运用链法则和关系式,这些量亦可以用其他参数表出。
设是
的任意参数表示且与
有相同的定向,则
其中再次用到,于是
与
有相同的,即它也是曲线的切向量,并且
切空间
①来自百度的定义
切空间是在某一点所有的切向量组成的线性空间。切空间是微分流形在一点处所联系的向量空间,是欧式空间中光滑曲线的切线、光滑曲面的切平面的推广。
代数几何定义
设为由根理想生成元
定义的仿射簇,则
在点
的切空间为线性簇
该切空间与生成元的选取无关
②来自梅向明的《微分流形和黎曼几何》的定义
 切空间与切映射
切空间与切映射
1.中一点处的切向量
设是
中的一点,所谓
点附近的
函数
是指定义在
的某个邻域
上的
函数,我们在
点附近的所有的
函数中定义一种等价关系:函数
,当且仅当在
的某点邻域中
.用
表示
代表的等价类,每个等价类为
点处一个
函数芽(germ)。a点处的全体
函数芽的集合用
来表示。
定义1
即由点邻域函数的运算诱导处函数芽得到运算,因此,
点处
函数芽构成向量空间
如果再定义
则构成实数域上的代数。
为了书写方便,以后用到芽时,省去括号只写
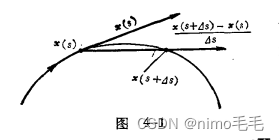
在中以
点为起点的全体向量构成一个
维向量空间,即
在
点处的切空间,集成
。显然有同构关系
设表示由原
中标准正交基平移到
所得到的
的一组标准正交基,则
中任一向量
可以表示为、
设,用
来表示函数
在
点沿方向
的方向导数。因为
依赖于
,点
及方向
,因此用
表示更好,这样
当给定后,任一
唯一地确定了一个实数
。因此
定义了映射
用表示这个映射是合理的,我们称
为
方向的方向导子,由于
,所以只要知道
在坐标函数
上的值,向量
和映射
就完全确定了。
由于导数的性质,容易看出,如果,
,则
2.导子空间
定义2 命表示具有上述性质(1)、(2)的映射
的全体,即
满足条件(1)、(2)
这些称为
的导子(derivation)
如果对于定义
其中右边的运算是在中进行的,那么容易证明
是实数域
上的向量空间,我们称它的导子空间。
定理1 (向量空间的同构)
为了证明定理,先给出两个引理
引理1 命是
中任一导子,
是
的某领域中的常值函数,则
.
证明:因为是线性的,只须证明:如果1表示取值为1的常函数,则
。注意
引理2 命是在某开集
上定义的
一函数,如果
,则存在
的一个领域
,以及定义在
上的
一函数
使得
证明:命是
的一个球域,注意对于
因此,
命
这些是函数且满足要求的两个条件。||
定理的证明:由于给定了,就唯一确定了
,这样决定了一个映射
(1)此映射是一一的。因为,如果有,则对于
,有
,也别对坐标函数
有
设则
即
(2)此映射保持代数结构。若,则对任意的
,有
(3)此映射是在上的,即要证明对于,存在
,使得
任给,设
是坐标函数,再设
,考虑向量
,它对应的导子为
,有
另一方面,根据引理2,在的定义域中的某个开球
上,有
所以
由于是任意的,所以
定理允许我们把在一点
处的切空间
与导子空间
等同起来,在这种等同下,
的标准基
等同于
,其中
是在坐标轴方向上的方向导子,即
做了这种等同之后,可以将号去掉,
将写成
,今后欧氏空间给了我们关于在一点切空间的几何直观,而在形式定义和证明中。我们将利用上面对的思想:在一点的一个切向量,是在
上的满足导子乘积法则(也称为Leibniz法则)的线性算子。对于切向量的这种观点,除了它的形式化和抽象性外,它相对地更容易运用,我们将利用这种观点吧切向量推广到微分流形上。
3.流形上的切向量
定义3 是
的
维流形,
,
是
点处全体
实函数芽的集合,则
在
点的切向量是实值函数
满足
其中
定义4 在
点的全体切向量的集合记成
或
或
。当规定
运算法则后,构成向量空间,称为
在
点的切空间
不难验证此定义是合理的。
下面要给出切向量在局部坐标系下的坐标表示。
设是包含a点的局部坐标系,其中坐标为
定义
其中是
中的坐标函数,容易验证
是
在
点处的切向量。
引理8 设是
的局部坐标,且使
。则对于
,存在
个函数
使得
而且在的某个邻域中
证明可参看引理2
定理2 设是
流形,点
附近的局部坐标为
,如果
,则
而且形成
的一组基
证明:设,在局部坐标系下,如果
可令
,则
而且
设的常值函数芽,则
再根据引理3:
最后在证明是线性无关的就够了,设
则
所以,线性无关,构成
的一组基
由此可见,n维流形在器上任一点处存在唯一的切空间,在局部坐标系下,它是由为基张成的n维向量空间,由于我们采取了“导子”的抽象定义,显而易见,切向量与切空间的概念与坐标系的选取无关,在不同的局部坐标系下,他们只不过有不同的坐标表示罢了
设是
的局部坐标域,且
,并且
是
的坐标函数,
是
的坐标函数,则在
处,对于
这就是坐标变换之下基变换的公式。
积流形
积流形是由两个微分流形的笛卡尔积所形成的流形
来自百度的概念
这边给出的定义就是“两个微分流形的笛卡尔积”
那么什么是笛卡尔积呢?
笛卡尔积指的是数学中,两个集合和
的笛卡尔,又称直积,记录为
,第一个对象是
的成员二第二个对象是
的所有可能有序对的其中一个成员
假设集合,集合
则两个集合的笛卡尔乘积为
列维-奇维塔联络
①来自百度的定义
列为奇维塔联络联络,在黎曼几何中,是切丛上的无绕率联络,它保持黎曼度量(或伪黎曼流形)不变,在黎曼流形和伪黎曼流形的理论中,共变导数一词经常用于列维奇维塔联络,联络的空间坐标表达式为克里斯托菲尔符
定义
配有的黎曼流形
的等距无扰联络
定义为
,则称
的列维奇维塔联络
②来自中国徐森林的《流形》
博主注:
Emmmmm,其实博主一直打算的是直接截图贴上去,而不是再浪费时间在打字一边,但是我不再打字一边的话,很多书籍因为扫描文件的问题,很多字母区分不开来,如i和j,l和i,所以我自己再打一遍也是校对,也是在加深学习的印象,但是这本书扫描的还行,而且公式太多了,我不是太想用LaTeX打出来了,所以就在这里截图贴上来了。







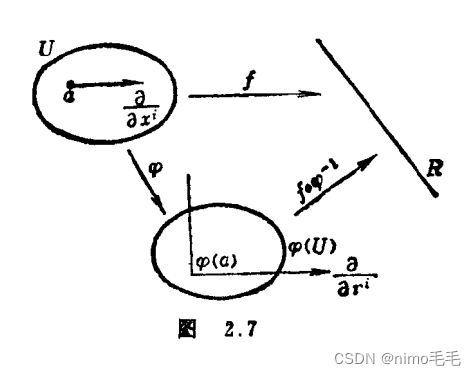
光滑映射
①来自百度的定义
设和
为光滑流形,
为
中开集,若对
的任意坐标映射
满足
为欧几里得空间的光滑函数,则称
为光滑映射
若为
中任意子集,则
若能扩张为
,其中
为
的开集,且
,则成为光滑映射
②来自中国苏况存的《流形的拓扑学》的定义
1.2 光滑函数和光滑映射
我们以开始就说过,光滑流形是这样的空间,在它上面可以讨论光滑函数,做法是很清楚的,令为光滑流形,
。我们说
在
点邻近是光滑的,如果有
点附近的坐标点
和
点附近的局部坐标
使映射
在
邻近光滑,这就是有意义的,因为我们谈的是欧氏空间之间的映射。相容性保证了这定义与所用的局部坐标无关,特别若是
,我们就不需要
而说有一个光滑函数
是
的一个局部表示,若
是覆盖
的一族局部坐标,就有定义
上的局部表示
,这些函数之间有以下关系
成为局部坐标的迁移函数(transition funktion),反之,若函数
并是上述相容性条件成立,则定义在
上的局部函数
在
上是相互协调的,从而定义了一个整体函数
,整体的函数时常是这样从相容的局部的东西“粘”出来的,既然
是定义在
的子集
上的,这就是经典的情况,但是采用整体的观点能对问题得到更好的展望,举例如下:
复变函数论中经典的Liouville定理指出,在平面上全纯而且有界的函数必是常数(想到代数学基本定理可以由此推出,你们会同意这是一个重要的定理),下面是经典的证法,将
展开成为幂级数
它在全平面上收敛,取一个以为心、
为半径的圆
,有
若,很容易估计出
既然r是任意的,当时候有
,即
是常数
我们要把Liouville定理作为解释为关于整体函数的一般事实,首先回顾一下可去奇点
引理 若在原点的邻域
中全纯但原点除外(即在
中全纯)而且当
时
,则
可拓展为
的全纯函数。
证 拓展如下
R是围绕0的圆(例如参看Ahlfors[1]p/100,中译本 p.122).
把看成Riemann球:
,它有局部坐标
,其中
为恒等映射,
为恒同映射,
定义为
我们看到,在上,迁移函数
正是
因为在上
,
是全纯的,这就使
成为一个复流形(Riemann球)
若在全平面
上全纯,则它在
上定义局部函数
利用相容性,在
上定义
为
.
因为有界,所以条件
显然成立,于是可拓展到
上,
定义一个
上的整体全纯函数
然而紧复流形上的任意整体全纯函数必定是以场数,因为一方面这种函数之模必有最大值(紧性),另一方面,极值原理指出,任意的局部极大值都不可能存在,这些例子也表明了群传理论和光滑理论根本不同,在紧光滑流形上当然有很多非常值的整体光滑函数。
我们又看到,已给一个光滑流形,笛卡尔乘积
也可构成光滑流形
定义 Lie群G既是一个群,作为一个空间的光滑流形,而且群运算
是光滑映射
例如是一个Lie群,条件
可从熟知的举证乘法公式
得出,是
和
的光滑函数
现在我们可以形式地定义光滑流形的范畴:对光滑映射若有另一光滑映射
使
则
称为微分同胚(diffeomorphism),这就是光滑流形范畴中的同构(isomorphism)。类似地,也有拓扑范畴中的同构(即同胚)、
范畴、
范畴等都各有其范畴,这些理论的最终目的是解决两个对象的
同构与否,但是很少的几个例子就已看到,目前这还是一句空话,关于这一点,我们还得学习汗多只是才能谈到一点实质性的东西
博主注:这边还有最后一段最后提醒,但是没啥大用,所以就不引用了
向量的代数计算
来自中国杨文茂和李全英的《微分几何的理论与问题》的讲解






向量的微分计算
来自中国杨文茂和李全英的《微分几何的理论与问题》的讲解


Frobenius定理
来自美国F.W.瓦内尔的《微分流形与李群基础》
1.60 定理(Frobenius) 令是
上的一个c维的
对合分布,令
,那么存在
的一个过
的积分流形,实际上,存在一个以
为中心,以
为坐标函数的立方体坐标系
使得片
(1) =常数,所有
都是的积分流形,而且如果
是
连通积分流形使得
,那么
位于这些片之一中
我这次就没有讲解关于"外代数"的内容,因为个人认为外代数的内容更加复杂,而且其拓展出来的知识点将会更多,所以我在这里就省略了"外代数"的讲解,这一次拖更的太久了,实在抱歉,学业比较忙
资料来源:
1.黎曼流形_百度百科
2.黎曼度量_百度百科
3.知乎:关于Riemannian metric | 黎曼度量 - 知乎
4.《泛函分析》——[苏联] Д.В.Кангороеич和Г.П.Акилов
5.知乎:从三维空间衍生而来的数学空间——距离空间(度量空间) - 知乎
6.度量空间_百度百科
7.《黎曼几何初步》——[中国]伍鸿熙
8.《微分几何讲义》——[中国]陈省身
9.《微分流形和黎曼几何》——[中国]梅向明
10.列维奇维塔联络_百度百科
11.《流形》——[中国]徐森林
12.《微分流形初步》——[中国]陈维恒
13.《流形的拓扑学》——[中国]苏况存
14.《微分流形和李群基础》——[美国]F.W.瓦内尔
这篇关于代数几何导引(德文版)【瑞士 马库斯·布罗德曼(Markus Brodmann)】的读书笔记,翻译和感想(3)-知识点的补充与拓展的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









