Kaggle泰坦尼克之灾

本文主要是介绍Kaggle泰坦尼克之灾，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

逻辑回归应用之Kaggle泰坦尼克之灾

背景

训练和测试数据是一些乘客的个人信息以及存活状况，要尝试根据它生成合适的模型并预测其他人的存活状况。

1. 数据总览

train.csv和test.csv分别为训练集和测试集,ground_truth.csv为对应答案
得到这些后，对这些数据读入和简单分析一下

df = pd.read_csv("train.csv")print(df.head())
df.info()
print(df.describe())

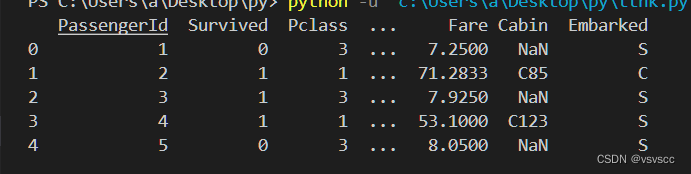
头5条数据
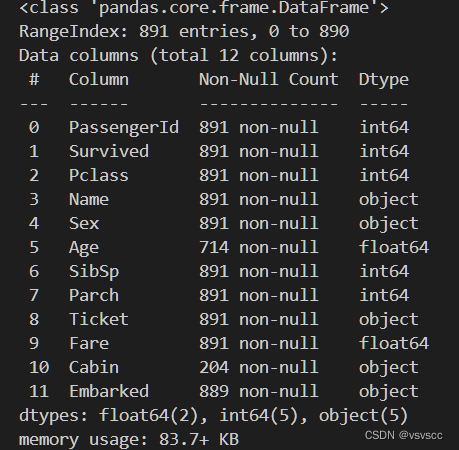
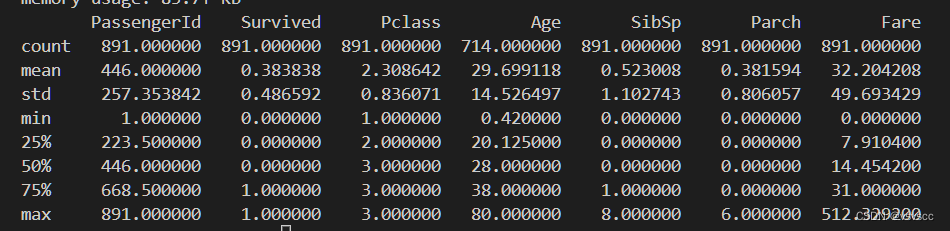
在这里插入图片描述

简单分析可以得出Age、Cabin、Embarked、Fare几个特征存在缺失值，大概0.383838的人最后获救了，2/3等舱的人数比1等舱要多，平均乘客年龄大概是29.7岁

数据初步分析

先看下每个属性与Survived的关系


```python
fig = plt.figure()
fig.set(alpha=0.2) # 设定图标透明度plt.subplot2grid((2,3),(0,1))#把几个小图放在一个大图里面
df.Pclass.value_counts().plot(kind="bar") # 柱状图 
plt.ylabel(u"人数")
plt.title(u"乘客等级分布")plt.subplot2grid((2,3),(0,0)) 
df.Survived.value_counts().plot(kind='bar')
plt.title(u'获救情况(1为获救)')
plt.ylabel(u'人数')plt.subplot2grid((2,3),(0,2))
plt.scatter(df.Survived, df.Age)
plt.ylabel(u"年龄")                         
plt.grid(b=True, which='major', axis='y') # 绘制网格线
plt.title(u"按年龄看获救分布 (1为获救)")plt.subplot2grid((2,3),(1,0), colspan=2)
df.Age[df.Pclass == 1].plot(kind='kde')  
df.Age[df.Pclass == 2].plot(kind='kde')
df.Age[df.Pclass == 3].plot(kind='kde')
plt.xlabel(u"年龄")
plt.ylabel(u"密度") 
plt.title(u"各等级的乘客年龄分布")plt.subplot2grid((2,3),(1,2))
df.Embarked.value_counts().plot(kind='bar')
plt.title(u"各登船口岸上船人数")
plt.ylabel(u"人数")plt.show()

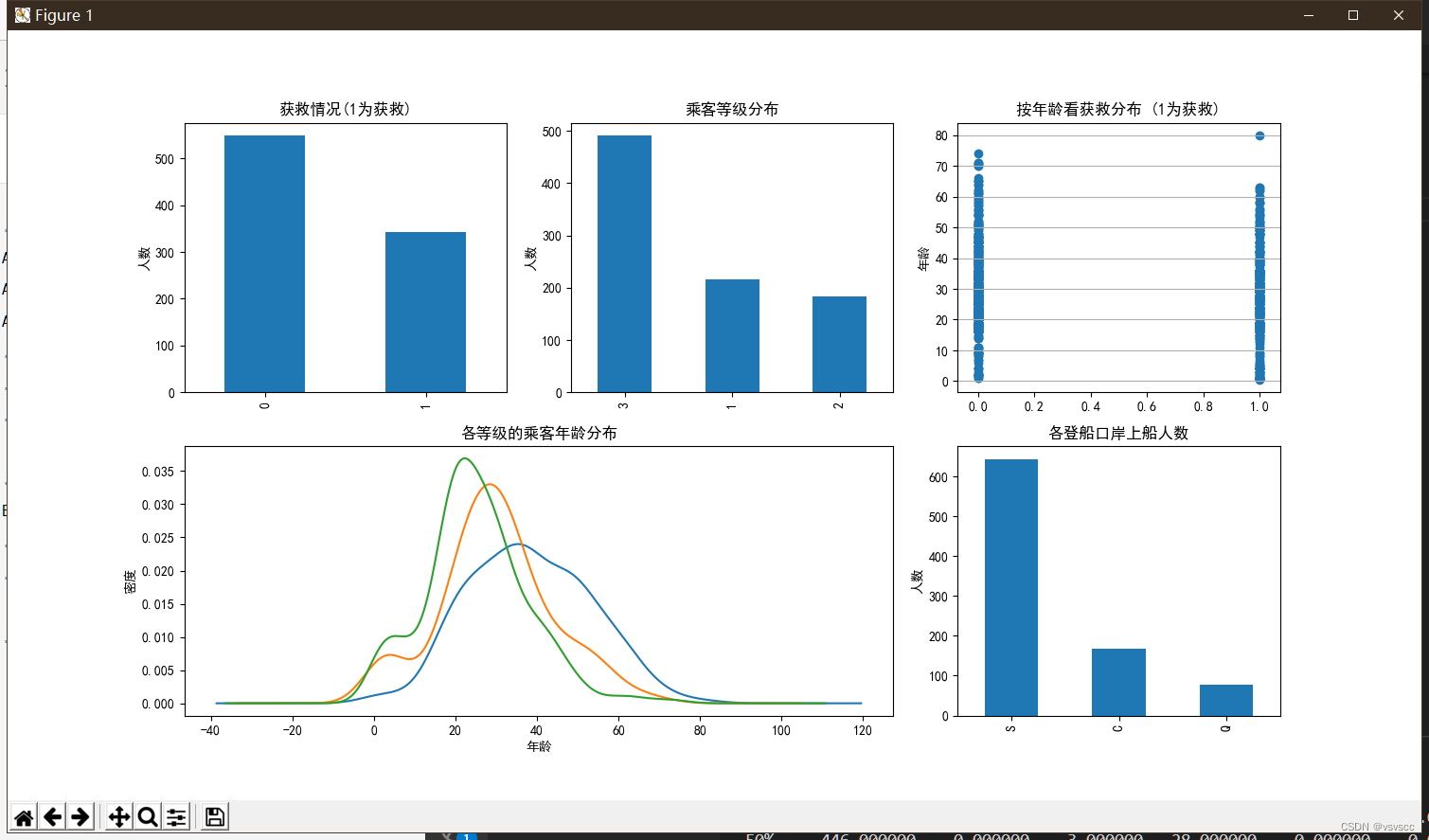
在这里插入图片描述
从图中我们可以得到一些信息：
1：超过一半的人没有获救
2：获救者在3等仓的人数比较多
3：从年龄分布可以看出，遇难和获救的乘客年龄分布都比较离散，跨度大
4：三个不同舱的乘客年龄总体趋势大致相同，其中20岁左右的乘客主要集中再二三等舱，一等舱中40岁左右的最多
5：s港上船的人数最多
我们可以通过这些数据假设获救可能和舱位等级有关系，可能和年龄有关系，也可能和登港的港口有关系…

先看一下各乘客等级的获救情况

fig = plt.figure()
fig.set(alpha=0.2)  Survived_0 = df.Pclass[df.Survived == 0].value_counts()
Survived_1 = df.Pclass[df.Survived == 1].value_counts()
df = pd.DataFrame({u'未获救':Survived_0, u'获救':Survived_1})
df.plot(kind='bar', stacked=True)
plt.title(u'不同等级乘客获救情况')
plt.xlabel(u'乘客等级')
plt.ylabel(u'人数')
plt.show()

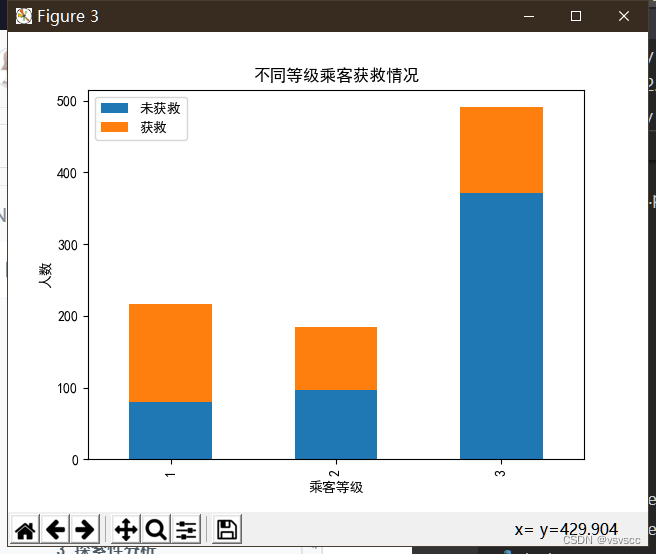
在这里插入图片描述
从图中可以看出，等级为1的乘客，获救的概率最大，并且随着等级的递减，获救的概率也是递减！所以，乘客等级这必然是一个影响乘获救的重要特征

查看各性别的获救情况

fig = plt.figure()
fig.set(alpha=0.2)Survived_0 = df.Survived[df.Sex == 'male'].value_counts()
Survived_1 = df.Survived[df.Sex == 'female'].value_counts()
df = pd.DataFrame({u'男性':Survived_0, u'女性':Survived_1})
df.plot(kind='bar', stacked=True)
plt.title(u'不同性别乘客获救情况')
plt.xlabel(u'获救与否')
plt.ylabel(u'人数')
plt.show()

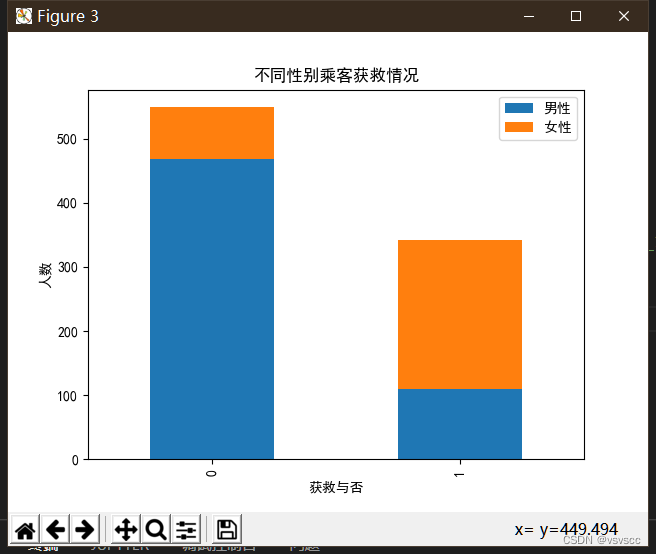
在这里插入图片描述
从上图可以很明显的发现女性的获救概率远远大于男性，果然女士优先执行的是真的

查看各登船港口的获救情况

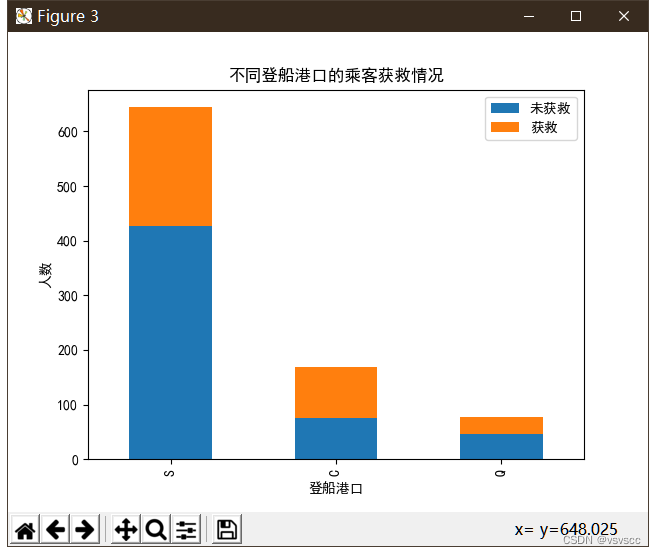
在这里插入图片描述
其中C港口最高，Q次之，S港口最低，应该也可以作为影响生还的一个因素

查看携带家人数量不同的获救情况

fig = plt.figure(figsize=(10,15))
fig.set(alpha=0.2)
Survived_0 = df.SibSp[df.Survived == 0].value_counts()
Survived_1 = df.SibSp[df.Survived == 1].value_counts()
df = pd.DataFrame({u'未获救':Survived_0, u'获救':Survived_1})
df.plot(kind='bar', stacked=True)
plt.title(u'携带不同家人数量的乘客获救情况')
plt.xlabel(u'携带家人数量')
plt.ylabel(u'人数')
plt.show()

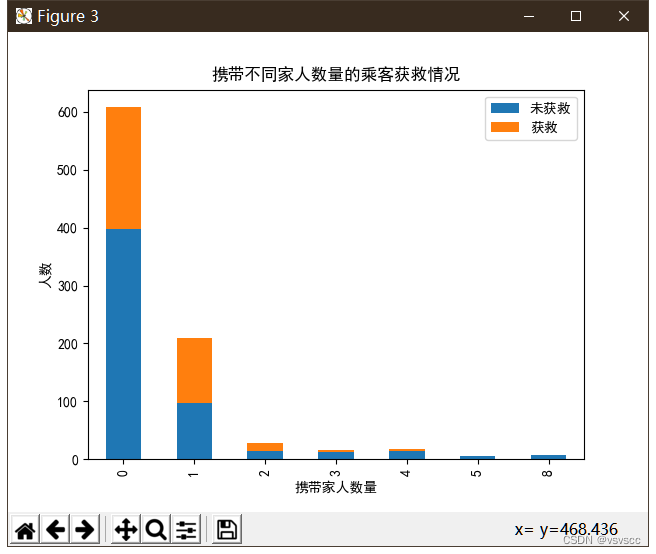
在这里插入图片描述
图上貌似看不出什么我们对他在处理

print(df[['SibSp','Survived']].groupby('SibSp').mean())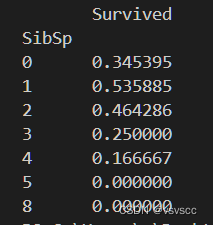

在这里插入图片描述
貌似有一个或者两个家人或者朋友的存活率跟高点，这应该也是影响是否被救的一个条件之一

查看船舱类型不同的获救情况

船舱类型的有效数据只有200多条不足全部数据的二分之一，我们将该数据舍弃

查看票的费用情况和获救的情况

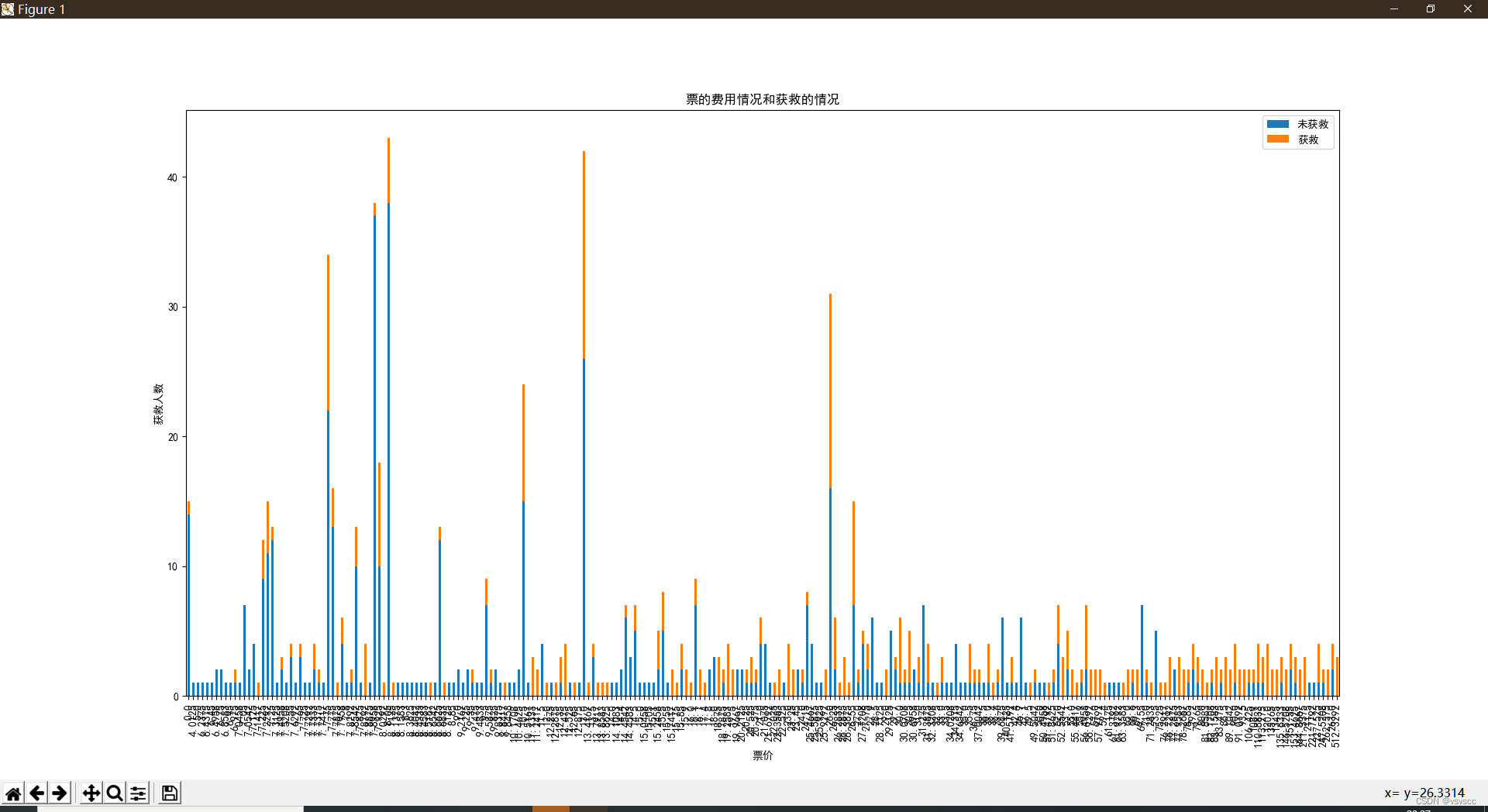
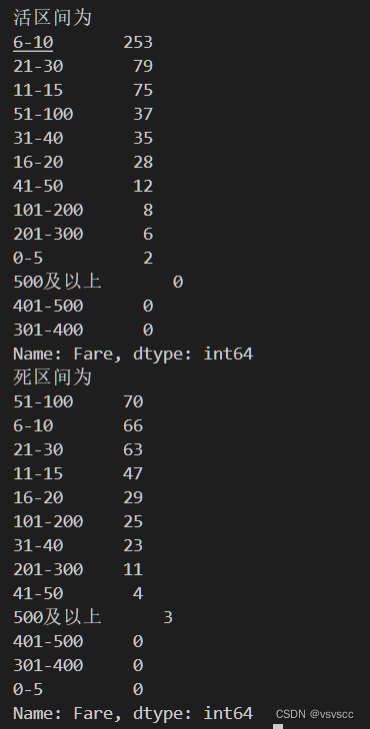
在这里插入图片描述

明显可以看出价格高的被救的概率也达低价票的基本都死翘翘，船票价格也是影响被救的因素之一

在看了全部有的数据之后我们在对数据处理

1.首先就是缺失值处理

处理Embarked和数据
Embarked只缺失两个，所以用众数填充即可

在做数据操作前我们先将训练集和测试集合并

#合并数据集
train_and_test = df.append(dt, sort=False) # 合并训练集与测试集
PassengerId = test['PassengerId']
train_and_test.shape

df.Embarked[df.Embarked.isnull() == True] = df.Embarked.dropna().mode().values

对Fare 用均值填充

其他数据采用森林模型预测填充

# 把已有的数值型特征取出来丢进Random Forest Regressor中
age_df = train_and_test[['Age', 'Fare', 'Parch', 'SibSp', 'Pclass']]
# 乘客分成已知年龄和未知年龄两部分
known_age = age_df[age_df.Age.notnull()].values
unknown_age = age_df[age_df.Age.isnull()].values
# y即目标年龄
y = known_age[:, 0]
# X即特征属性值
X = known_age[:, 1:]
# fit到RandomForestRegressor之中
rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
rfr.fit(X, y)
# 用得到的模型进行未知年龄结果预测
predictedAges = rfr.predict(unknown_age[:, 1::])
# 用得到的预测结果填补原缺失数据
train_and_test.loc[(train_and_test.Age.isnull()), 'Age'] = predictedAges
train_and_test.info()

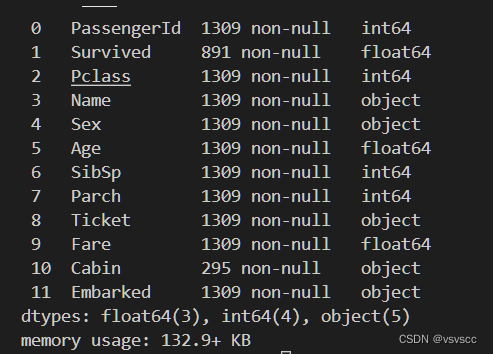
在这里插入图片描述

数据清洗，提取训练字段

因为逻辑回归建模时，需要输入的特征都是数值型特征，我们通常会先对类目型的特征因子化。我们使用pandas的”get_dummies”来完成这个工作，并拼接在原来的数据上

cols = ['Embarked', 'Sex', 'Pclass']
train_and_test = pd.get_dummies(train_and_test, columns=cols, prefix_sep='__')

对于cabin的缺失值，我们将缺失值为0有值的为1

train_and_test.loc[train_and_test.Cabin.isnull(), 'Cabin'] = 'U0'
train_and_test['Cabin'] = train_and_test['Cabin'].apply(lambda x : 0 if x == 'U0' else 1)

建模及模型评价

划分训练集和测试集

index = PassengerId[0] - 1
train_and_test_drop = train_and_test.drop(['PassengerId', 'Name', 'Ticket'], axis=1)
train_data = train_and_test_drop[:index]
test_data = train_and_test_drop[index:]train_X = train_data.drop(['Survived'], axis=1)
train_y = train_data['Survived']
test_X = test_data.drop(['Survived'], axis=1)
test_y = dl['Survived']

随机森林

rfc = RandomForestClassifier()
rfc.fit(train_X, train_y)
pred_rfc = rfc.predict(test_X)
accuracy_rfc = roc_auc_score(test_y, pred_rfc) 
print("随机森林的预测结果：", accuracy_rfc)

模型得分在这里插入图片描述

逻辑回归

lr = LogisticRegression() # logit 逻辑回归
lr.fit(train_X, train_y)
pred_lr = lr.predict(test_X) 
accuracy_lr = roc_auc_score(test_y, pred_lr)
print("逻辑回归的预测结果：", accuracy_lr)

在这里插入图片描述
决策树

gbdt = GradientBoostingClassifier()
gbdt.fit(train_X, train_y)
pred_gbdt = gbdt.predict(test_X)
accuracy_gbdt = roc_auc_score(test_y, pred_gbdt) 
print("GBDT模型的预测结果：", accuracy_gbdt)