【SLAM学习】罗德里格斯公式推导详细过程

目前，在进实验室之前自己学习SLAM，用的是高翔博士所著的《视觉SLAM十四讲》，其中涉及到罗德里格斯公式，这里讲自己的推导过程记录如下。

罗德里格斯公式如下：

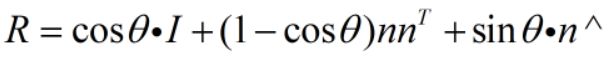
上述公式是在视觉SLAM中常用的公式，可以讲旋转角变换为旋转矩阵，其中R为旋转矩阵，θ为绕轴旋转的角度，n为旋转轴方向的单位向量。

下面给出推导过程：

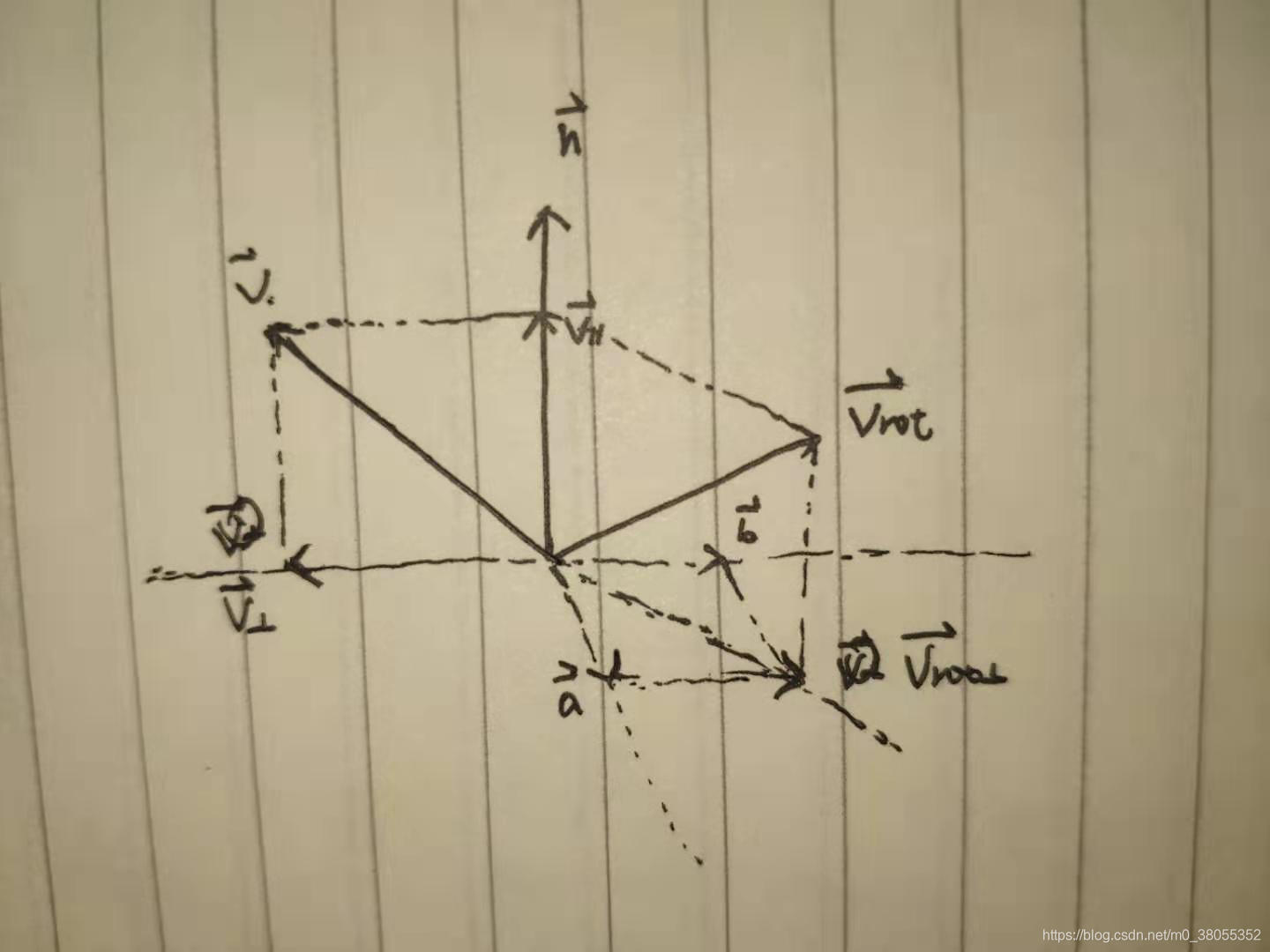
这是一个证明的辅助示意图（比较粗糙，不要见怪），大致是利用了向量的分解以及一些叉乘的知识。

证明

因为我们的最终目的是要的到旋转矩阵R，而所用到R的地方就是v_rot =Rv，我们就要尽可能的用v来表示v_rot。
v_rot = v_⊥ + v_//
v_rot = a + b + v_//
然后我们就把 a,b,v_// 分别用 v 来表示就好了。
首先是 v_//，从简单到难嘛，很容易看出来
v_// = (v·n)·n
解释一下，v·n是一个内积，也就是向量v在n上的投影，是一个数，然后再数乘n，变成一个方向和n相同，大小为v·n的向量，也就是v_//.

然后是b，也不难看出
b = cosθ·v_⊥
这又是怎么得出来的呢，下面给出简单的推导。
b 应该是长度为 v_rot 的膜乘-cosθ，方向与 v_⊥ 相反，那么
b = ||v_rot⊥||·(-cosθ)·（-v_⊥n）
这里注意cosθ是负的，继续推导，由于||v_rot⊥||与||v_⊥||相等，
b = ||v_⊥||·cosθ·v_⊥n
b = cosθ·v_⊥

最后是a，先给出a的结果
a = sinθ · n × v
与 b 的推导一样，a 的长度是 ||v_rot⊥||·sinθ，方向是 n×v_⊥n，那么
a = ||v_rot⊥||·sinθ·n×v_⊥n
又因为上面提到的||v_rot⊥||与||v_⊥||相等，所以
a = ||v_⊥||·sinθ·n×v_⊥n
a = sinθ·n×v_⊥
但是，由于我们最终要表现得形式是 v_rot 和 v 之间的，所以把上述a的表示变成由v表示，注意到，n× v_⊥ 是膜为||n||·||v_⊥||·sin90° = ||n||·||v_⊥||，方向为n×v的向量，而 n × v 同样也是，所以直接替换
a = sinθ · n × v

到此为止，就把所有的向量用与 v 有关的向量来表示了，目前的推导公式已经变成了如下样子：

v_rot = sinθ·n×v + cosθ·v_⊥ + (v·n)·n

然而，此时还并没有转换为 v_rot = Rv的形式，下面就要把所有的 v 的系数转化为矩阵。

首先第一项，可以直接利用叉乘进行转化，如果你看过《视觉SLAM十四讲》就对这个肯定不陌生，可以转化为 sinθ·n^·v，
其中，n^大概就是左边矩阵的这个样子，这是规定好的，可以算一下，这样算出来和直接叉乘的结果一致，图中的 k 即为我所说的 n。

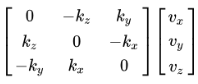
然后第二项，v_⊥ = v - v_//
所以原式 = cosθ·(v - (v·n)·n)，就转化为了对第三项进行变换

最后是第三项，由数乘的交换律，(v·n)·n = n·(v·n)，然后由于v·n = n^T·v，所以原式转化为n·n^T·v，前半部分转化为矩阵。

综上所述，最终可得（剩下的自己顺着写就出来了）

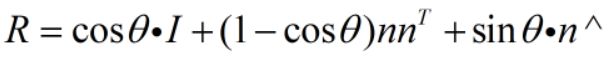
如有问题，欢迎留言~~~