本文主要是介绍二分查找 红蓝染色法 【基础算法精讲 04】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
视频链接 :
二分查找 红蓝染色法_哔哩哔哩_bilibili
在排序数组中查找元素的第一个和最后一个位置
链接 :
在排序数组中查找元素的第一个和最后一个位置
思想 :
暴力 :
在lc上,直接暴力枚举左端点和右端点也是能够通过的!
二分 :
题目要求在O(log n)的时间复杂度处理该问题,那么就要用到二分的思想了!
设l,r为要找的区间的左右端点

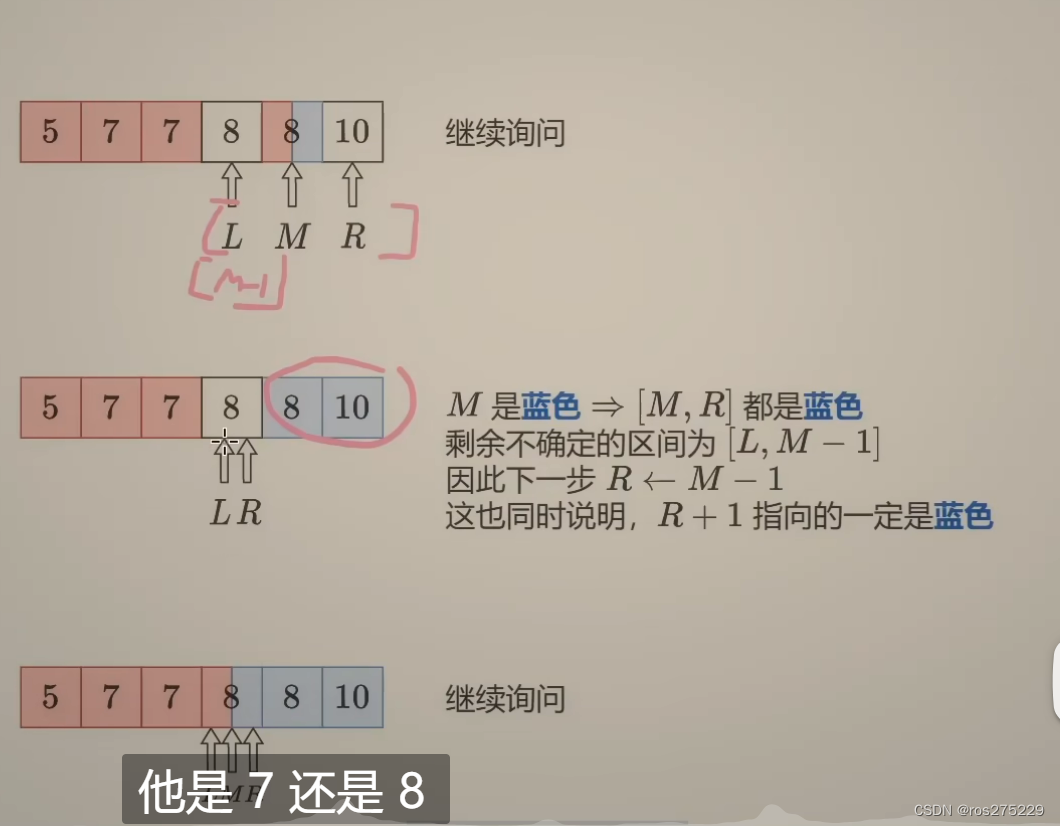
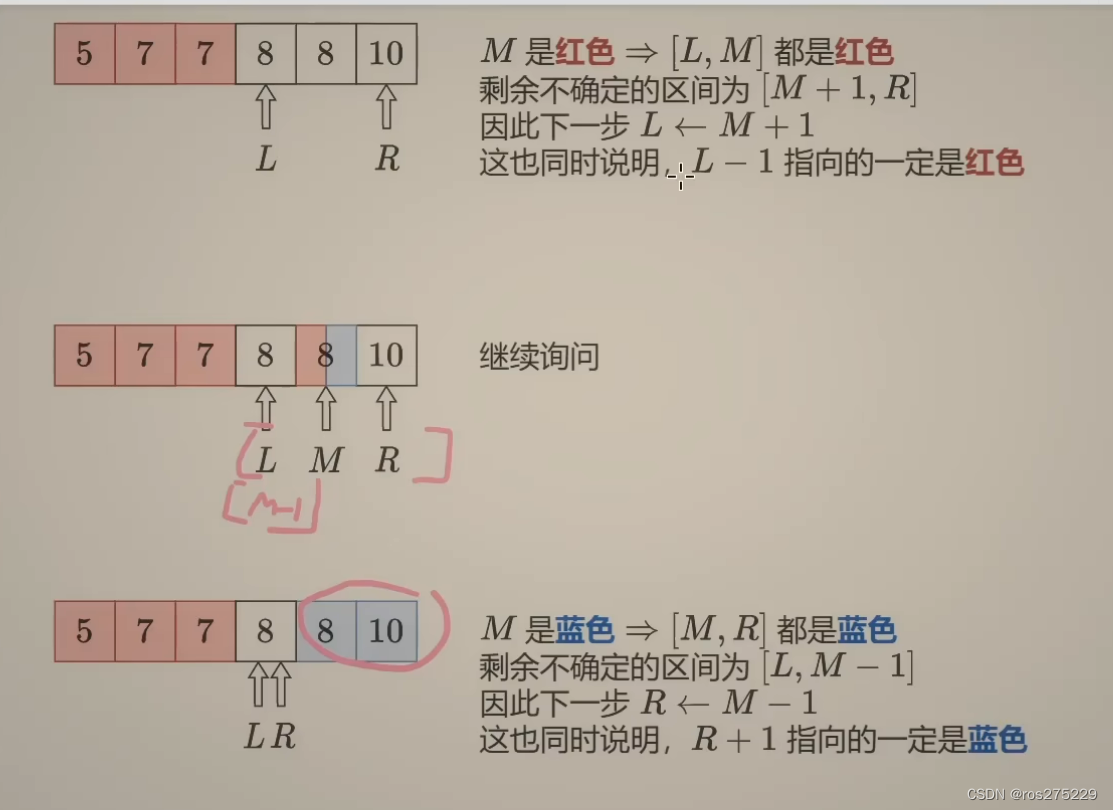
代码 :
1.暴力 (c++)
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int n=nums.size();int ans1=-1,ans2=-1;int num=0;if(n==0){ans1=-1;ans2=-1;}if(n==1){if(nums[0]==target){ans1=0;ans2=0;}else{ans1=-1;ans2=-1;} }if(n>=2){for(int i=0;i<n;i++){if(nums[i]==target)num++;}if(num==0){ans1=-1;ans2=-1;}if(num==1){for(int i=0;i<n;i++){if(nums[i]==target){ans1=i;ans2=i;}}}if(num>=2){for(int i=0;i<n;i++){if(nums[i]==target){ans1=i;break;}}for(int j=n-1;j>=0;j--){if(nums[j]==target){ans2=j;break;}}}}return {ans1,ans2};}
};2.二分(python)
# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空,或者所有数都 < target,则返回 len(nums)
# 要求 nums 是非递减的,即 nums[i] <= nums[i + 1]# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1 # 闭区间 [left, right]while left <= right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right+1] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right]else:right = mid - 1 # 范围缩小到 [left, mid-1]return left # 或者 right+1# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:left = 0right = len(nums) # 左闭右开区间 [left, right)while left < right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right)else:right = mid # 范围缩小到 [left, mid)return left # 或者 right# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:left, right = -1, len(nums) # 开区间 (left, right)while left + 1 < right: # 区间不为空mid = (left + right) // 2# 循环不变量:# nums[left] < target# nums[right] >= targetif nums[mid] < target:left = mid # 范围缩小到 (mid, right)else:right = mid # 范围缩小到 (left, mid)return right # 或者 left+1class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:start = lower_bound(nums, target) # 选择其中一种写法即可if start == len(nums) or nums[start] != target:return [-1, -1]# 如果 start 存在,那么 end 必定存在end = lower_bound(nums, target + 1) - 1return [start, end]3.二分(c++)
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int leftBorder = getLeftBorder(nums, target);int rightBorder = getRightBorder(nums, target);// 情况一if (leftBorder == -2 || rightBorder == -2) return {-1, -1};// 情况三if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};// 情况二return {-1, -1};}
private:int getRightBorder(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] > target) {right = middle - 1;} else { // 寻找右边界,nums[middle] == target的时候更新leftleft = middle + 1;rightBorder = left;}}return rightBorder;}int getLeftBorder(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新rightright = middle - 1;leftBorder = right;} else {left = middle + 1;}}return leftBorder;}
};这篇关于二分查找 红蓝染色法 【基础算法精讲 04】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








