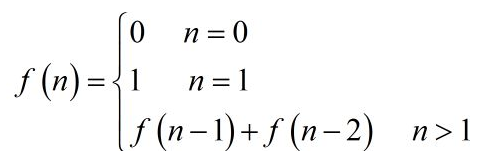本文主要是介绍【算法】斐波那契数列的效率问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
点击这个链接:(斐波那契数列)是在数学中非常有名的一个数列形式,无论是数学界还是编程圈无不在拿它讲解递归调用的思想,数学公式如下:
现在通过编程实现“斐波那契数列”程序,通过传入的数值n,拿到第n位下斐波那契数列的值。
正如在课本中所讲解到的,通过“递归调用”来实现该方法,代码实现可以设计为:
public Long Fibonacci(int n)
{if(n <= 0)return 0;if(n == 1)return 1;//递归实现调用return Fibonacci(n-1) + Fibonacci(n-2);
}
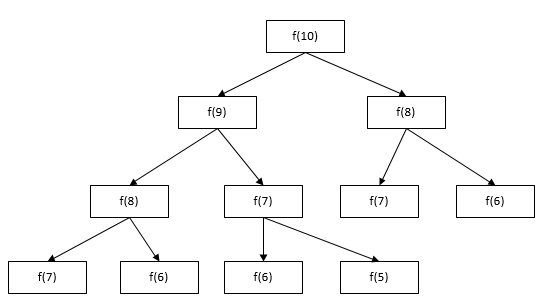
如图所示,是通过递归实现“斐波那契”的原理图:
由图可见,仅仅是对f(10)进行计算的原理图,而且仅仅画出了4层,就出现了相同结果的大量重复,如果计算f(100),这种单纯的递归实现就会出现严重的性能问题。即随着n值的递增,为求出最终的f(n),重复的项会急剧增加。用递归计算这种方法的时间复杂度是以n的指数方式递增。
问题分析:
(1)之所以递归调用实现“斐波那契数列”慢,是因为计算过程中大量的中间量的重复,之所以出现重复,在于从上向下计算的这个过程,计算每一个数,结合上图,都需要向下层去请求一个完整的二叉树中的值,类似高中物理中学习过的“核裂变的链式反应”,这就是问题所在。
解决思路:
(1)结合上图,采用从下向上的计算策略,即可保证相同的数不需要重复去计算,因为中间出现过的变量值,已经计算出来而且进行保存,就可以快速地拿来使用,如果查找不存在, 再去计算。即由f(0)和f(1)算出f(2),由f(1)和f(2)算出f(3)……,最终这样下来,计算的时间复杂度为O(n)。
优化方案:
public Long Fibonacci(int n)
{int result[2] = {0,1}if(n < 2)return result[n];long fibNMinusOne = 1;long fibNMinusTwo = 0;long fibN = 0;for(int i=2; i <= n; i++){fibN = fibNMinusOne + fibNMinusTwo;fibNMinusTwo = fibNMinusOne;fibNMinusOne = fibN;}return fibN;
}如上代码所示,结合“斐波那契数列”原理图,不再是从上向下进行计算,而是从下向上计算,这样就会省略大量的中间重复的项的计算过程,也优化了通过“递归”实现计算结果的方法。
写在最后:
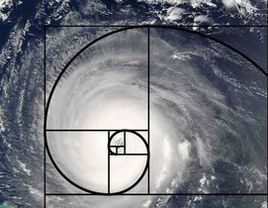
“斐波那契”实现的图形,被称为黄金比例图形,很美,如图是斐波那契螺旋线:
That's all.
这篇关于【算法】斐波那契数列的效率问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!