越复杂的CoT越有效吗？Complexity-Based Prompting for Multi-step Reasoning

本文主要是介绍越复杂的CoT越有效吗？Complexity-Based Prompting for Multi-step Reasoning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Complexity-Based Prompting for Multi-step Reasoning

论文：https://openreview.net/pdf?id=yf1icZHC-l9
Github：https://github.com/FranxYao/chain-of-thought-hub
发表位置：ICLR 2023
Complexity-Based Prompting for Multi-step Reasoning（ICLR2023）.pdf

本文提出Complexity-CoT，目标是挑选合适的exemplar作为CoT prompt来引导大模型进行推理。挑选exemplar则从reasoning path的复杂性，并结合self-consistency采样实现构建CoT prompt。

一、动机

目前超过100B的大模型具备涌现能力，即可以在一些复杂的任务上完成推理，且效果高于原先的监督训练策略。目前Chain-of-Thought（CoT）通过生成简短的文本来表示推理路径，从而更好地引导大模型完成复杂问题的推理，例如math word problem等。
构建CoT目前需要一些标注样本作为exemplar，本文提出Complexity-CoT，旨在从example selection角度构建CoT推理路径。

Example selection is a central problem in the prompting literature

先前的样本挑选策略是基于规则、采样等方法。本文则从推理路径（reasoning chain）的复杂性来进行样本挑选。

二、方法

提出的方法如下图所示：

提出方法的先验假设： We hypothesize that language models’ reasoning performance will increase if we use complex instances as in-context “training example,” as they intuitively subsume simpler instances。即假设提供的上下文示例（In-Context exemplar）中的推理路径足够的复杂，那么在这些exemplar组成的prompt下引导大模型推理的效果会更好）

（1）复杂性定义
那么如何定义推理路径的复杂性？本文在输入提示上对每一个推理步骤用“\n”进行分割，即推理路径中“\n”分割后的句子数量（代表推理的步骤）可以作为复杂度。
对于一些没有推理路径的样本，也可考虑Question的长度等。
另外也可以考虑推理中所涉及到的公式长度。

（2）复杂性的混杂因素（Cofounder）
输入的prompt中，所有推理步骤和每个样本的推理步骤数量对推理的影响。实验发现，每个样本的推理步数是相对于混杂因素而言性能提升的最主要来源。

（3）基于复杂性的一致性（Complexity-based Consistency）
现有证据表明，生成式大模型可以在推理过程中走捷径，依赖于训练数据中不可避免地存在的虚假相关性。这通常会导致对未见过的数据的泛化效果不佳。
因此，借鉴Self-Consistency，对于一个测试样本，采样生成 $N = 50$ 个推理路径。Self-Consistency的策略是从这 $N$ 个推理路径中进行投票选择，即挑选预测答案数量最多的作为最终结果。

本文提出的基于复杂性的一致性方法中，会先对这 $N$ 个推理路径进行复杂性量化，并获得复杂性Top $K$ 个路径。此时这 $K$ （取值在30～40之间）个推理路径都包含很多步骤。随后在这 $K$ 推理路径中进行统计投票挑选。

三、实验

数学运算评测数据集：

GSM8K
MultiArith
MathQA

常识推理

StrategyQA
Date Understanding
Penguins

模型

LaMDA
PaLM
Minerva
GPT-3
Codex

实验结果：

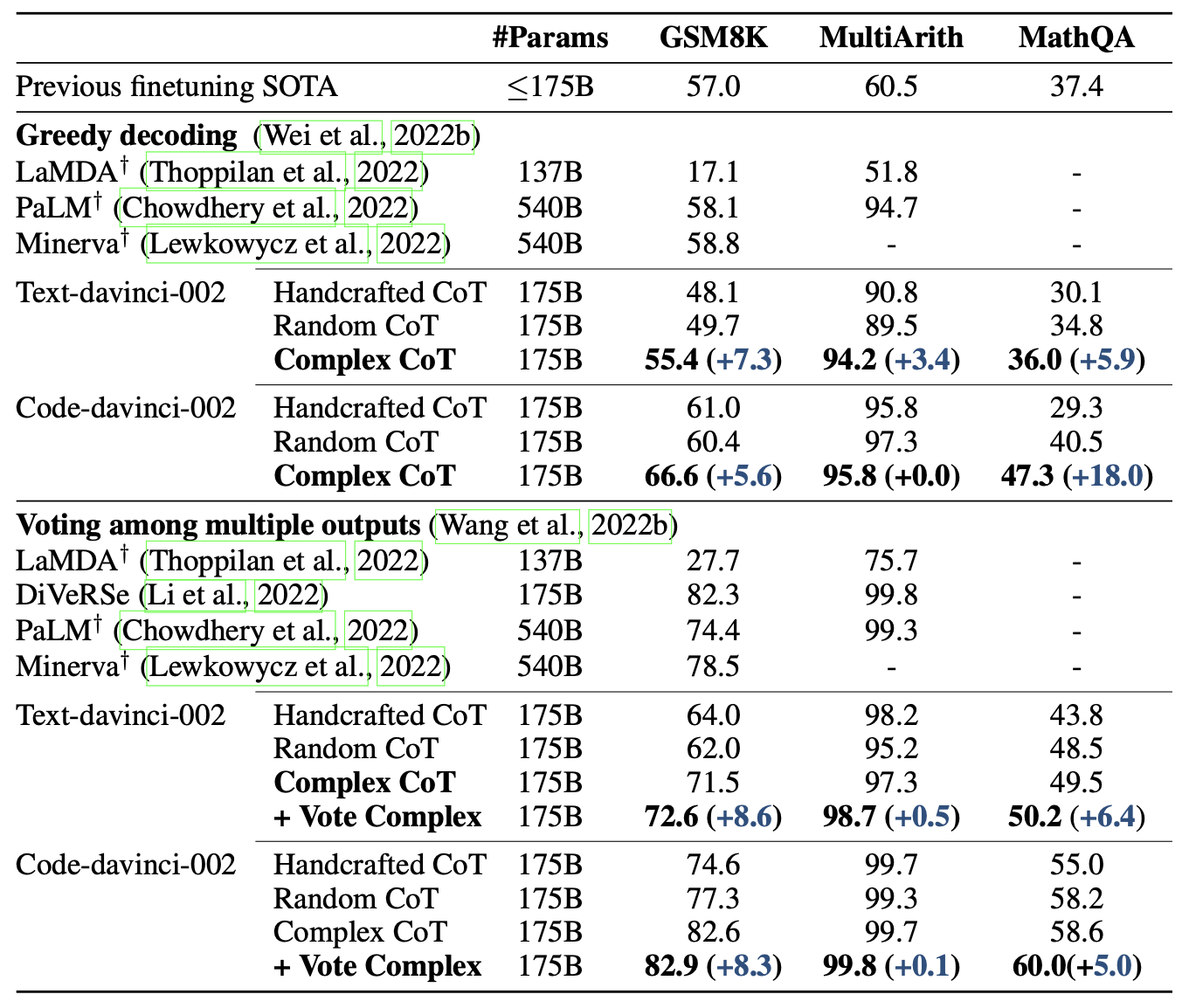
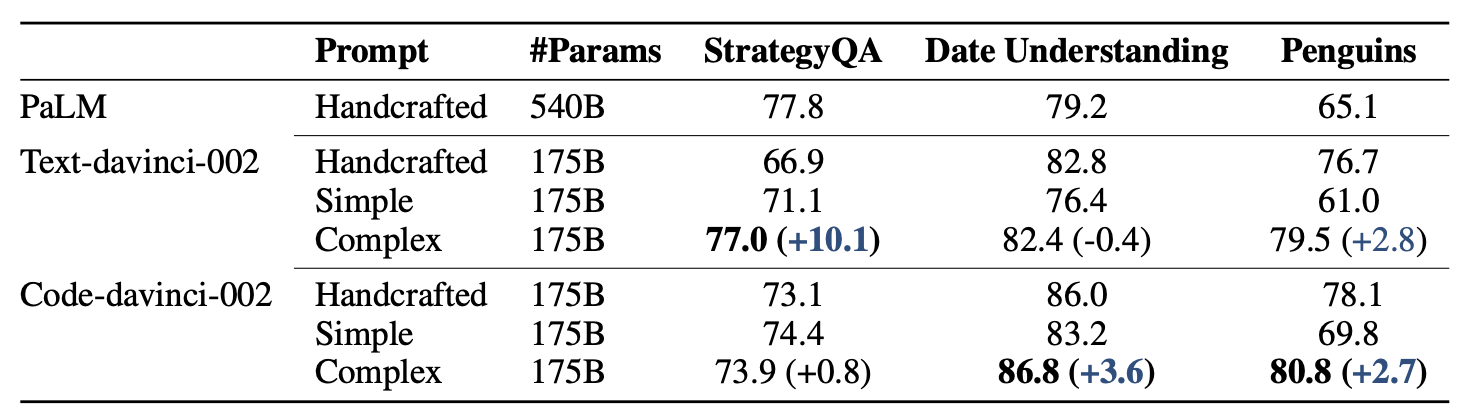
Greedy Decoding：标准的CoT，只推理一次，
Voting：Self-Consistency方法，采样多个推理路径并进行投票。

实验结果可知：

构建ICL exemplar时考虑高复杂性的样本有助于提高模型的推理性能；
在投票阶段，砍掉低复杂性的推理路径也可以大大提高模型预测的准确性
说明大语言模型不论时提示工程，还是采样投票集成阶段，考虑CoT推理路径的复杂性是有必要的。

下面在验证集上进行实验，验证先前的假设“提供的上下文示例（In-Context exemplar）中的推理路径足够的复杂，那么在这些exemplar组成的prompt下引导大模型推理的效果会更好”

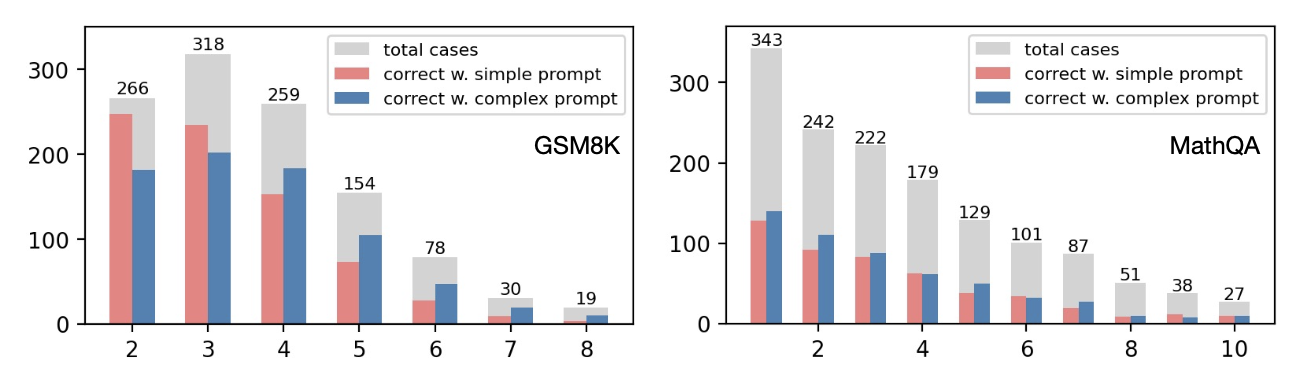
横坐标表示验证样本预测结果的推理路径长度，灰色表示对应路径长度的样本总数量，红色表示对应预测路径长度下使用低复杂性的CoT prompt且预测正确的样本数量，蓝色则为对应预测路径长度下使用高复杂性的CoT prompt且预测正确的样本数量。
可以发现，GSM8K任务中，低复杂性的CoT prompt适合预测简单的样本，高复杂性的CoT prompt则适合预测较难的样本。相比之下，MathQA则都是复杂性高的CoT prompt更占优势。

四、实现

以GSM8K数据集为例，CoT prompt样例如下所示：

Question: Angelo and Melanie want to plan how many hours over the next week they should study together for their test next week. They have 2 chapters of their textbook to study and 4 worksheets to memorize. They figure out that they should dedicate 3 hours to each chapter of their textbook and 1.5 hours for each worksheet. If they plan to study no more than 4 hours each day, how many days should they plan to study total over the next week if they take a 10-minute break every hour, include 3 10-minute snack breaks each day, and 30 minutes for lunch each day?
Let's think step by step
Angelo and Melanie think they should dedicate 3 hours to each of the 2 chapters, 3 hours x 2 chapters = 6 hours total.
For the worksheets they plan to dedicate 1.5 hours for each worksheet, 1.5 hours x 4 worksheets = 6 hours total.
Angelo and Melanie need to start with planning 12 hours to study, at 4 hours a day, 12 / 4 = 3 days.
However, they need to include time for breaks and lunch. Every hour they want to include a 10-minute break, so 12 total hours x 10 minutes = 120 extra minutes for breaks.
They also want to include 3 10-minute snack breaks, 3 x 10 minutes = 30 minutes.
And they want to include 30 minutes for lunch each day, so 120 minutes for breaks + 30 minutes for snack breaks + 30 minutes for lunch = 180 minutes, or 180 / 60 minutes per hour = 3 extra hours.
So Angelo and Melanie want to plan 12 hours to study + 3 hours of breaks = 15 hours total.
They want to study no more than 4 hours each day, 15 hours / 4 hours each day = 3.75
They will need to plan to study 4 days to allow for all the time they need.
The answer is 4Question: Mark's basketball team scores 25 2 pointers, 8 3 pointers and 10 free throws.  Their opponents score double the 2 pointers but half the 3 pointers and free throws.  What's the total number of points scored by both teams added together?
Let's think step by step
Mark's team scores 25 2 pointers, meaning they scored 25*2= 50 points in 2 pointers.
His team also scores 6 3 pointers, meaning they scored 8*3= 24 points in 3 pointers
They scored 10 free throws, and free throws count as one point so they scored 10*1=10 points in free throws.
All together his team scored 50+24+10= 84 points
Mark's opponents scored double his team's number of 2 pointers, meaning they scored 50*2=100 points in 2 pointers.
His opponents scored half his team's number of 3 pointers, meaning they scored 24/2= 12 points in 3 pointers.
They also scored half Mark's team's points in free throws, meaning they scored 10/2=5 points in free throws.
All together Mark's opponents scored 100+12+5=117 points
The total score for the game is both team's scores added together, so it is 84+117=201 points
The answer is 201Question: Bella has two times as many marbles as frisbees. She also has 20 more frisbees than deck cards. If she buys 2/5 times more of each item, what would be the total number of the items she will have if she currently has 60 marbles?
Let's think step by step
When Bella buys 2/5 times more marbles, she'll have increased the number of marbles by 2/5*60 = 24
The total number of marbles she'll have is 60+24 = 84
If Bella currently has 60 marbles, and she has two times as many marbles as frisbees, she has 60/2 = 30 frisbees.
If Bella buys 2/5 times more frisbees, she'll have 2/5*30 = 12 more frisbees.
The total number of frisbees she'll have will increase to 30+12 = 42
Bella also has 20 more frisbees than deck cards, meaning she has 30-20 = 10 deck cards
If she buys 2/5 times more deck cards, she'll have 2/5*10 = 4 more deck cards.
The total number of deck cards she'll have is 10+4 = 14
Together, Bella will have a total of 14+42+84 = 140 items
The answer is 140Question: A group of 4 fruit baskets contains 9 apples, 15 oranges, and 14 bananas in the first three baskets and 2 less of each fruit in the fourth basket. How many fruits are there?
Let's think step by step
For the first three baskets, the number of apples and oranges in one basket is 9+15=24
In total, together with bananas, the number of fruits in one basket is 24+14=38 for the first three baskets.
Since there are three baskets each having 38 fruits, there are 3*38=114 fruits in the first three baskets.
The number of apples in the fourth basket is 9-2=7
There are also 15-2=13 oranges in the fourth basket
The combined number of oranges and apples in the fourth basket is 13+7=20
The fourth basket also contains 14-2=12 bananas.
In total, the fourth basket has 20+12=32 fruits.
The four baskets together have 32+114=146 fruits.
The answer is 146Question: You can buy 4 apples or 1 watermelon for the same price. You bought 36 fruits evenly split between oranges, apples and watermelons, and the price of 1 orange is $0.50. How much does 1 apple cost if your total bill was $66?
Let's think step by step
If 36 fruits were evenly split between 3 types of fruits, then I bought 36/3 = 12 units of each fruit
If 1 orange costs $0.50 then 12 oranges will cost $0.50 * 12 = $6
If my total bill was $66 and I spent $6 on oranges then I spent $66 - $6 = $60 on the other 2 fruit types.
Assuming the price of watermelon is W, and knowing that you can buy 4 apples for the same price and that the price of one apple is A, then 1W=4A
If we know we bought 12 watermelons and 12 apples for $60, then we know that $60 = 12W + 12A
Knowing that 1W=4A, then we can convert the above to $60 = 12(4A) + 12A
$60 = 48A + 12A
$60 = 60A
Then we know the price of one apple (A) is $60/60= $1
The answer is 1Question: Susy goes to a large school with 800 students, while Sarah goes to a smaller school with only 300 students.  At the start of the school year, Susy had 100 social media followers.  She gained 40 new followers in the first week of the school year, half that in the second week, and half of that in the third week.  Sarah only had 50 social media followers at the start of the year, but she gained 90 new followers the first week, a third of that in the second week, and a third of that in the third week.  After three weeks, how many social media followers did the girl with the most total followers have?
Let's think step by step
After one week, Susy has 100+40 = 140 followers.
In the second week, Susy gains 40/2 = 20 new followers.
In the third week, Susy gains 20/2 = 10 new followers.
In total, Susy finishes the three weeks with 140+20+10 = 170 total followers.
After one week, Sarah has 50+90 = 140 followers.
After the second week, Sarah gains 90/3 = 30 followers.
After the third week, Sarah gains 30/3 = 10 followers.
So, Sarah finishes the three weeks with 140+30+10 = 180 total followers.
Thus, Sarah is the girl with the most total followers with a total of 180.
The answer is 180Question: Sam bought a dozen boxes, each with 30 highlighter pens inside, for $10 each box. He rearranged five of these boxes into packages of six highlighters each and sold them for $3 per package. He sold the rest of the highlighters separately at the rate of three pens for $2. How much profit did he make in total, in dollars?
Let's think step by step
Sam bought 12 boxes x $10 = $120 worth of highlighters.
He bought 12 * 30 = 360 highlighters in total.
Sam then took 5 boxes × 6 highlighters/box = 30 highlighters.
He sold these boxes for 5 * $3 = $15
After selling these 5 boxes there were 360 - 30 = 330 highlighters remaining.
These form 330 / 3 = 110 groups of three pens.
He sold each of these groups for $2 each, so made 110 * 2 = $220 from them.
In total, then, he earned $220 + $15 = $235.
Since his original cost was $120, he earned $235 - $120 = $115 in profit.
The answer is 115Question: In a certain school, 2/3 of the male students like to play basketball, but only 1/5 of the female students like to play basketball. What percent of the population of the school do not like to play basketball if the ratio of the male to female students is 3:2 and there are 1000 students?
Let's think step by step
The students are divided into 3 + 2 = 5 parts where 3 parts are for males and 2 parts are for females.
Each part represents 1000/5 = 200 students.
So, there are 3 x 200 = 600 males.
And there are 2 x 200 = 400 females.
Hence, 600 x 2/3 = 400 males play basketball.
And 400 x 1/5 = 80 females play basketball.
A total of 400 + 80 = 480 students play basketball.
Therefore, 1000 - 480 = 520 do not like to play basketball.
The percentage of the school that do not like to play basketball is 520/1000 * 100 = 52
The answer is 52

Question: Ivan has a bird feeder in his yard that holds two cups of birdseed. Every week, he has to refill the emptied feeder. Each cup of birdseed can feed fourteen birds, but Ivan is constantly chasing away a hungry squirrel that steals half a cup of birdseed from the feeder every week. How many birds does Ivan’s bird feeder feed weekly?
Let's think step by step
The squirrel steals 1/2 cup of birdseed every week, so the birds eat 2 - 1/2 = 1 1/2 cups of birdseed.
Each cup feeds 14 birds, so Ivan’s bird feeder feeds 14 * 1 1/2 = 21 birds weekly.
The answer is 21Question: Samuel took 30 minutes to finish his homework while Sarah took 1.3 hours to finish it. How many minutes faster did Samuel finish his homework than Sarah?
Let's think step by step
Since there are 60 minutes in 1 hour, then 1.3 hours is equal to 1.3 x 60 = 78 minutes.
Thus, Samuel is 78 – 30 = 48 minutes faster than Sarah.
The answer is 48Question: Julia bought 3 packs of red balls, 10 packs of yellow balls, and 8 packs of green balls. There were 19 balls in each package. How many balls did Julie buy in all?
Let's think step by step
The total number of packages is 3 + 10 + 8 = 21.
Julia bought 21 × 19 = 399 balls.
The answer is 399Question: Lexi wants to run a total of three and one-fourth miles. One lap on a particular outdoor track measures a quarter of a mile around. How many complete laps must she run?
Let's think step by step
There are 3/ 1/4 = 12 one-fourth miles in 3 miles.
So, Lexi will have to run 12 (from 3 miles) + 1 (from 1/4 mile) = 13 complete laps.
The answer is 13Question: Asia bought a homecoming dress on sale for $140. It was originally priced at $350. What percentage off did she get at the sale?
Let's think step by step
Asia saved $350 - $140 = $210 on the dress.
That means she saved $210 / $350 = 0.60 or 60% off on the dress.
The answer is 60Question: As a special treat, Georgia makes muffins and brings them to her students on the first day of every month.  Her muffin recipe only makes 6 muffins and she has 24 students.  How many batches of muffins does Georgia make in 9 months?
Let's think step by step
She has 24 students and her muffin recipe only makes 6 muffins so she needs to bake 24/6 = 4 batches of muffins
She brings muffins on the 1st of the month for 9 months and it takes 4 batches to feed all of her students so she bakes 9*4 = 36 batches of muffins
The answer is 36Question: Jorge bought 24 tickets for $7 each. For purchasing so many, he is given a discount of 50%. How much, in dollars, did he spend on tickets?
Let's think step by step
Jorge spent 24 tickets * $7 per ticket = $168 total.
After applying the discount, Jorge spent $168 * 0.50 = $84.
The answer is 84Question: OpenAI runs a robotics competition that limits the weight of each robot. Each robot can be no more than twice the minimum weight and no less than 5 pounds heavier than the standard robot. The standard robot weighs 100 pounds. What is the maximum weight of a robot in the competition?
Let's think step by step
the minimum is 5 more than 100 so 100+5=105
the maximum weight of a robot is twice the minimum 105*2=210
The answer is 210

实验脚本：
https://github.com/FranxYao/chain-of-thought-hub/blob/main/gsm8k/gpt3.5turbo_gsm8k_complex.ipynb

import openai
import re
import time
import numpy as np
from tqdm import tqdm
from datasets import load_dataset## 功能函数
from tenacity import (retry,stop_after_attempt,wait_chain,wait_fixed
) @retry(wait=wait_chain(*[wait_fixed(3) for i in range(3)] +[wait_fixed(5) for i in range(2)] +[wait_fixed(10)]))
def completion_with_backoff(**kwargs):return openai.ChatCompletion.create(**kwargs)
def test_answer(pred_str, ans_str):pattern = '\d*\.?\d+'pred = re.findall(pattern, pred_str)if(len(pred) >= 1):# print(pred_str)pred = pred[-1]gold = re.findall(pattern, ans_str)# print(ans_str)gold = gold[-1]return pred == goldelse: return Falsedef parse_pred_ans(filename):with open(filename) as fd: lines = fd.readlines()am, a = None, Nonenum_q, acc = 0, 0current_mode = 'none'questions = []ans_pred = []ans_gold = []for l in lines:if(l.startswith('Q: ')):if(am is not None and a is not None):questions.append(q)ans_pred.append(am)ans_gold.append(a)if(test_answer(am, a)):acc += 1current_mode = 'q'q = lnum_q += 1elif(l.startswith('A_model:')):current_mode = 'am'am = lelif(l.startswith('A:')):current_mode = 'a'a = lelse:if(current_mode == 'q'): q += lelif(current_mode == 'am'): am += lelif(current_mode == 'a'): a += lelse:raise ValueError(current_mode)questions.append(q)ans_pred.append(am)ans_gold.append(a)if(test_answer(am, a)):acc += 1print('num_q %d correct %d ratio %.4f' % (num_q, acc, float(acc / num_q)))return questions, ans_pred, ans_golddef test_finished(ans_model):if('answer is' in ans_model): return Trueelse: return Falsedef extract_ans(ans_model):ans_model = ans_model.split('\n')ans = []residual = []for li, al in enumerate(ans_model):ans.append(al)if('answer is' in al):breakresidual = list(ans_model[li + 1:])ans = '\n'.join(ans)residual = '\n'.join(residual)return ans, residualif __name__ == "__main__":## 获得数据openai.api_key = "sk-"gsm8k = load_dataset('gsm8k', 'main')validation_index = np.load('../gsm8k/lib_prompt/validation_index.npy')validation_data = gsm8k['train'].select(validation_index)gsm8k_test = gsm8k['test']## 获得Complex CoT promptprompt_complex = open('../gsm8k/lib_prompt/prompt_hardest.txt').read()## 贪心Decodingi = 0with open('outputs/test_gpt_3.5_turbo_complex_temp_0.txt', 'w') as fd:for q, a in tqdm(zip(gsm8k_test['question'], gsm8k_test['answer']), total=len(gsm8k_test['question'])):prompt_q = prompt_complex + '\nQuestion: ' + q + '\n'  response = completion_with_backoff(model="gpt-3.5-turbo",messages=[{"role": "system", "content": "Follow the given examples and answer the question."},{"role": "user", "content": prompt_q},],temperature=0)ans_model = response['choices'][0]['message']['content']ans_, residual = extract_ans(ans_model)fd.write('Q: %s\nA_model:\n%s\nA:\n%s\n\n' % (q, ans_, a))i += 1# if(i == 2): break