计算几何【三角剖分】

本文主要是介绍计算几何【三角剖分】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在几何中，三角剖分是指将平面对象细分为三角形，并且通过扩展将高维几何对象细分为单纯形。
对于一个给定的点集，有很多种三角剖分，如：
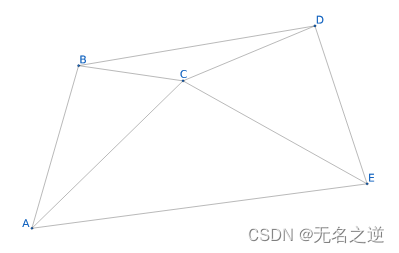
在这里插入图片描述

OI 中的三角剖分主要指二维几何中的完美三角剖分（二维 Delaunay 三角剖分，简称 DT）。

Delaunay 三角剖分

定义

在数学和计算几何中，对于给定的平面中的离散点集 $P$ ，其 Delaunay 三角剖分 DT( $P$ ) 满足：

空圆性：DT( $P$ ) 是唯一的（任意四点不能共圆），在 DT( $P$ ) 中，任意三角形的外接圆范围内不会有其它点存在。
最大化最小角：在点集 $P$ 可能形成的三角剖分中，DT( $P$ ) 所形成的三角形的最小角最大。从这个意义上讲，DT( $P$ ) 是 最接近于规则化 的三角剖分。具体的说是在两个相邻的三角形构成凸四边形的对角线，在相互交换后，两个内角的最小角不再增大。

性质

最接近：以最接近的三点形成三角形，且各线段（三角形的边）皆不相交。
唯一性：不论从区域何处开始构建，最终都将得到一致的结果（点集中任意四点不能共圆）。
最优性：任意两个相邻三角形构成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小角度不会变化。
最规则：如果将三角剖分中的每个三角形的最小角进行升序排列，则 Delaunay 三角剖分的排列得到的数值最大。
区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。
具有凸边形的外壳：三角剖分最外层的边界形成一个凸多边形的外壳。

构造 DT 的分治算法

DT 有很多种构造算法，在 $\log n)$ 的构造算法中，分治算法是最易于理解和实现的。

分治构造 DT 的第一步是将给定点集按照 $x$ 坐标升序排列，如下图是排好序的大小为 $10$ 的点集。

在这里插入图片描述

一旦点集有序，我们就可以不断地将其分成两个部分（分治），直到子点集大小不超过 $3$ 。然后这些子点集可以立刻剖分为一个三角形或线段。

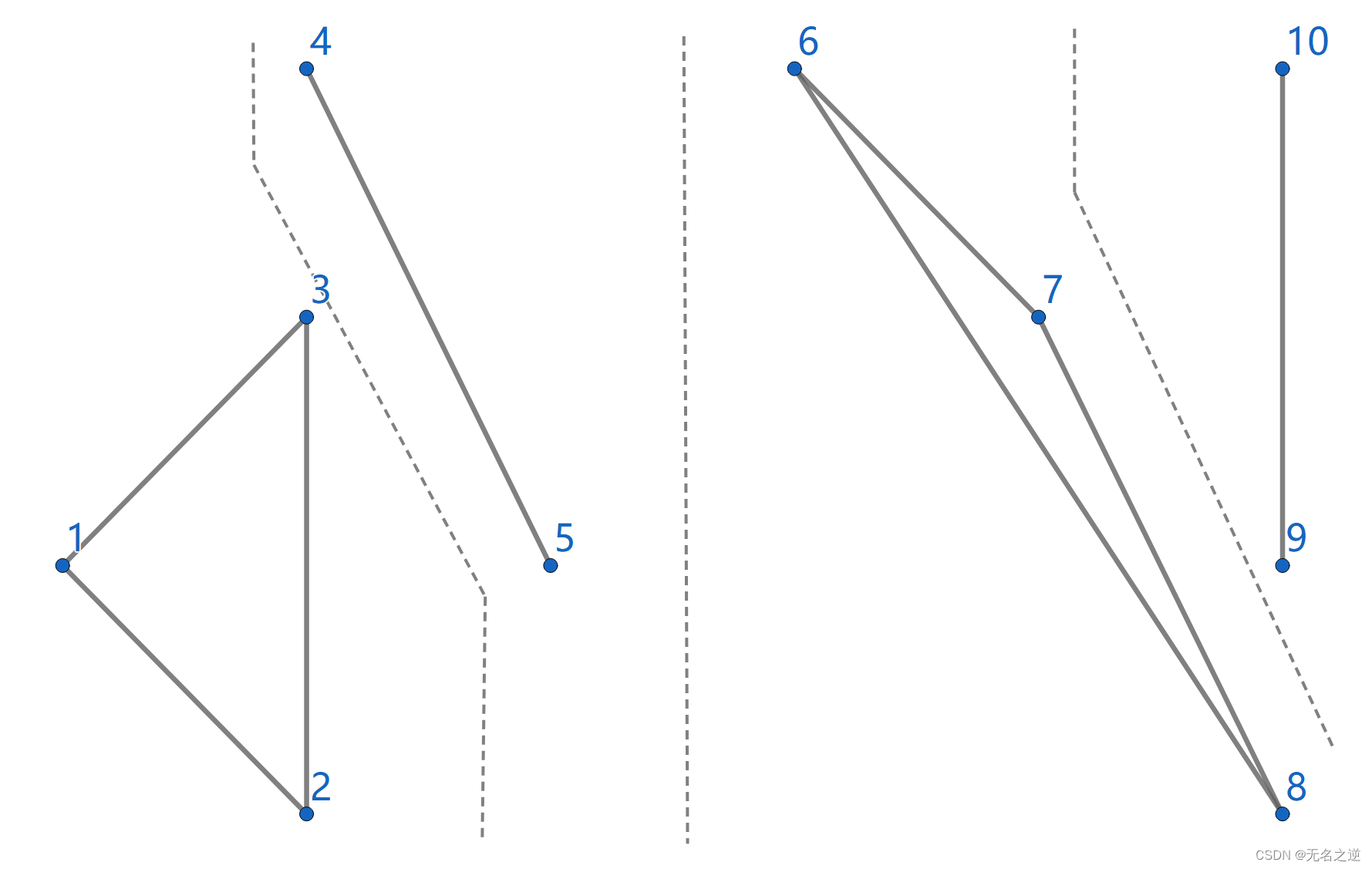
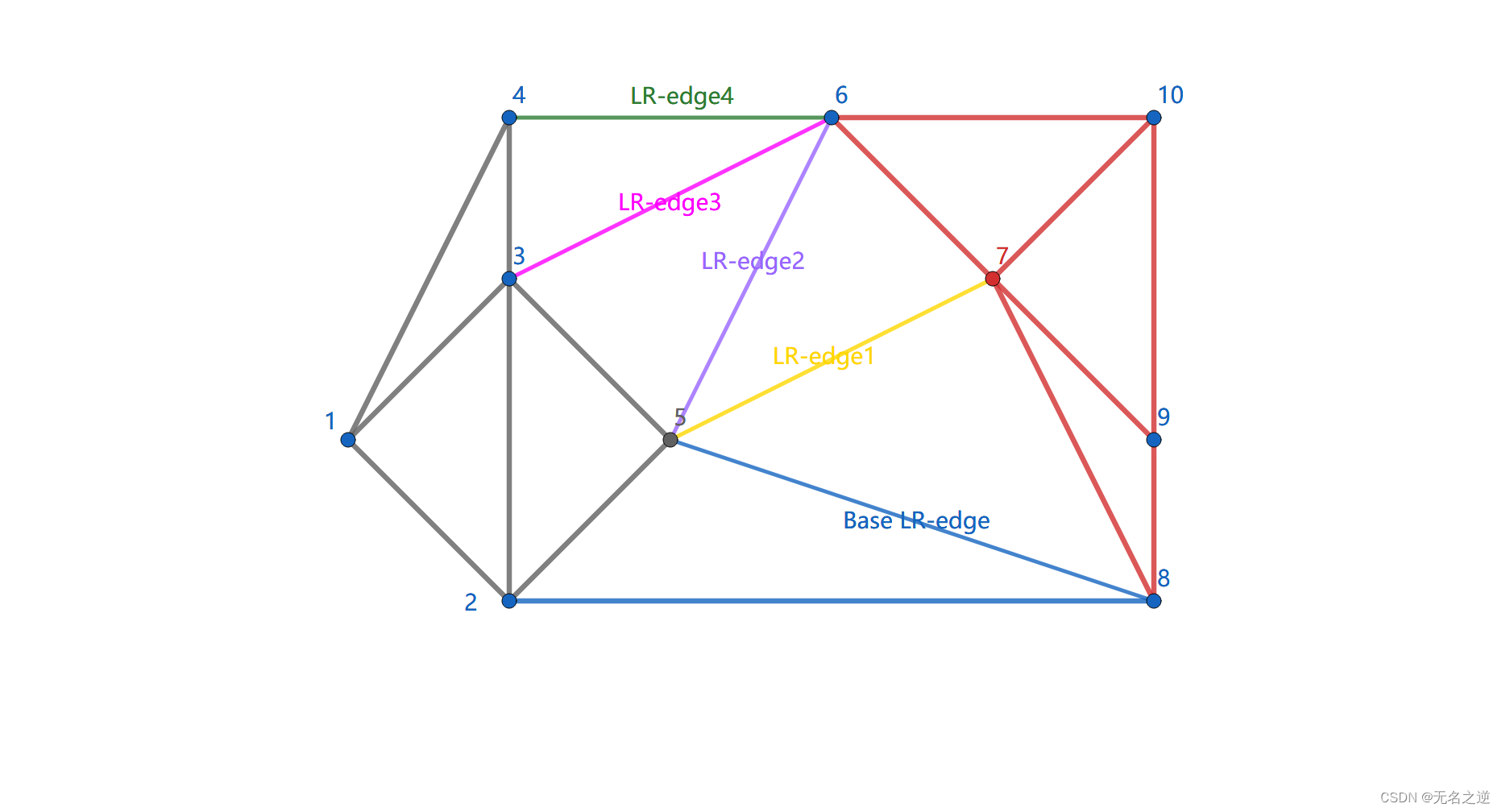
在这里插入图片描述

然后在分治回溯的过程中，已经剖分好的左右子点集可以依次合并。合并后的剖分包含 LL-edge（左侧子点集的边）。RR-edge（右侧子点集的边），LR-edge（连接左右剖分产生的新的边），如图 LL-edge（灰色），RR-edge（红色），LR-edge（蓝色）。对于合并后的剖分，为了维持 DT 性质，我们可能需要删除部分 LL-edge 和 RR-edge，但我们在合并时不会增加 LL-edge 和 RR-edge。

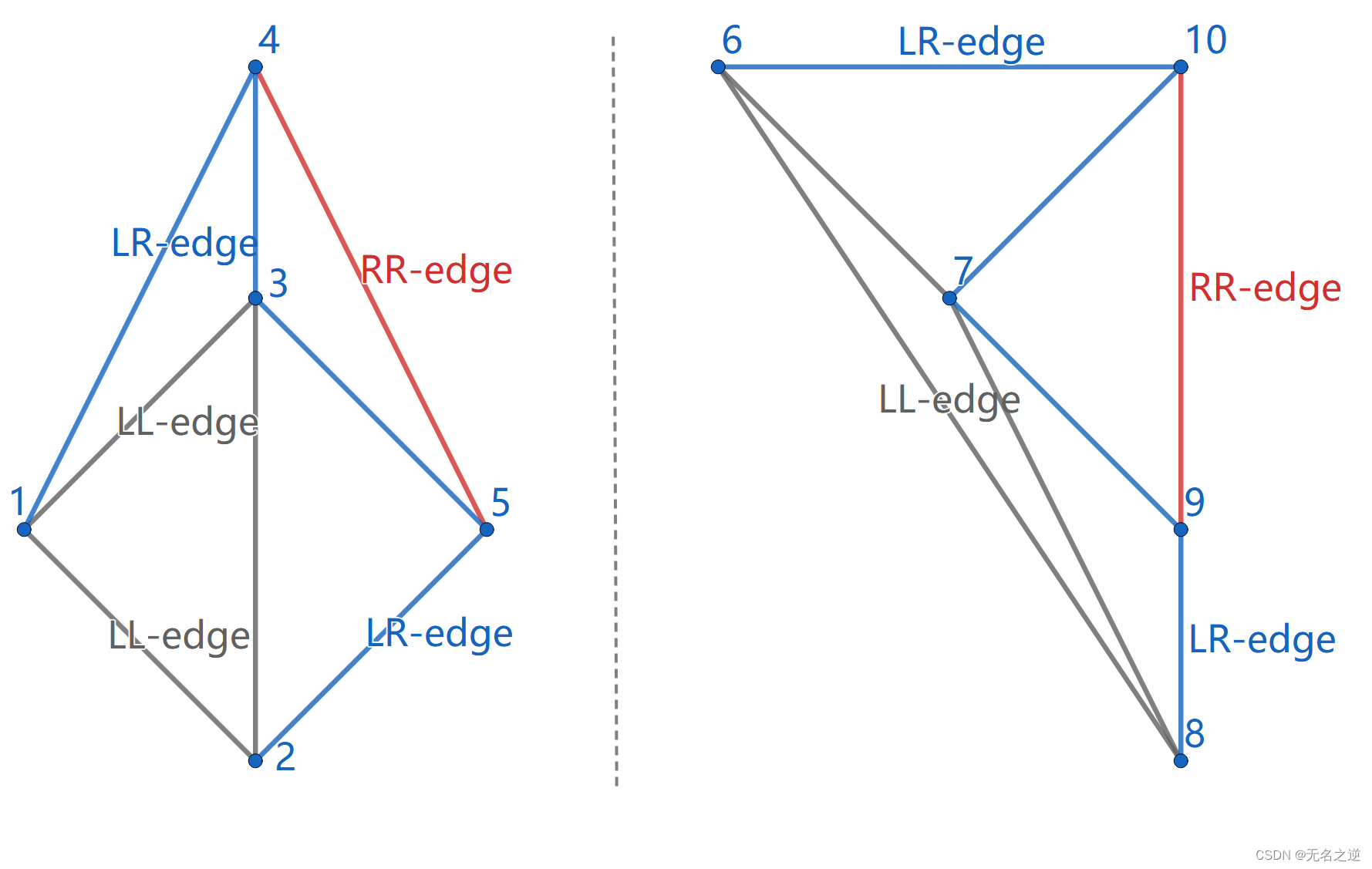
在这里插入图片描述

合并左右两个剖分的第一步是插入 base LR-edge，base LR-edge 是 最底部 的不与任何 LL-edge 及 RR-edge 相交的 LR-edge。

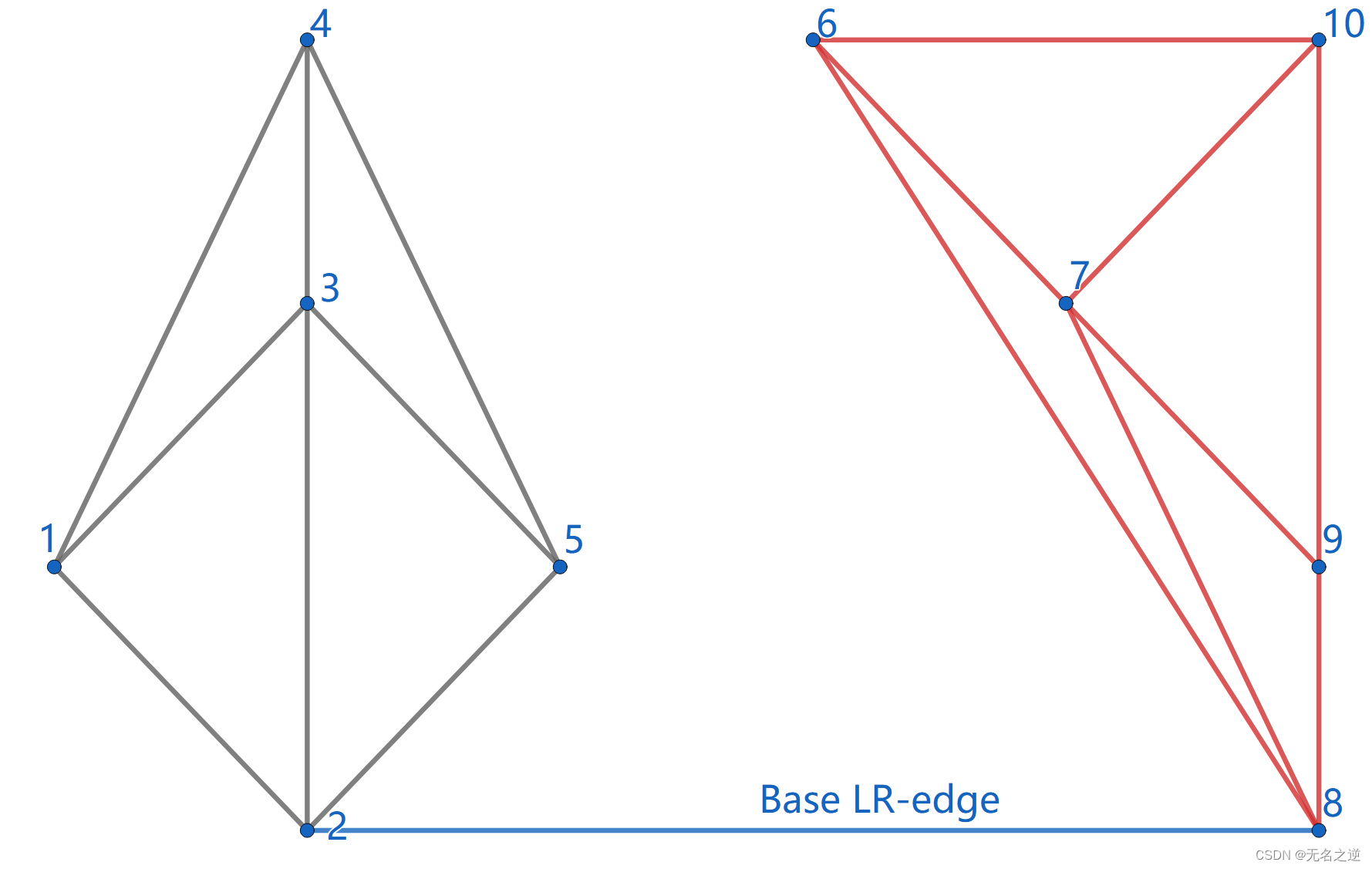
在这里插入图片描述

然后，我们需要确定下一条 紧接在 base LR-edge 之上的 LR-edge。比如对于右侧点集，下一条 LR-edge 的可能端点（右端点）为与 base LR-edge 右端点相连的 RR-edge 的另一端点（ $6, 7, 9$ 号点），左端点即为 $2$ 号点。

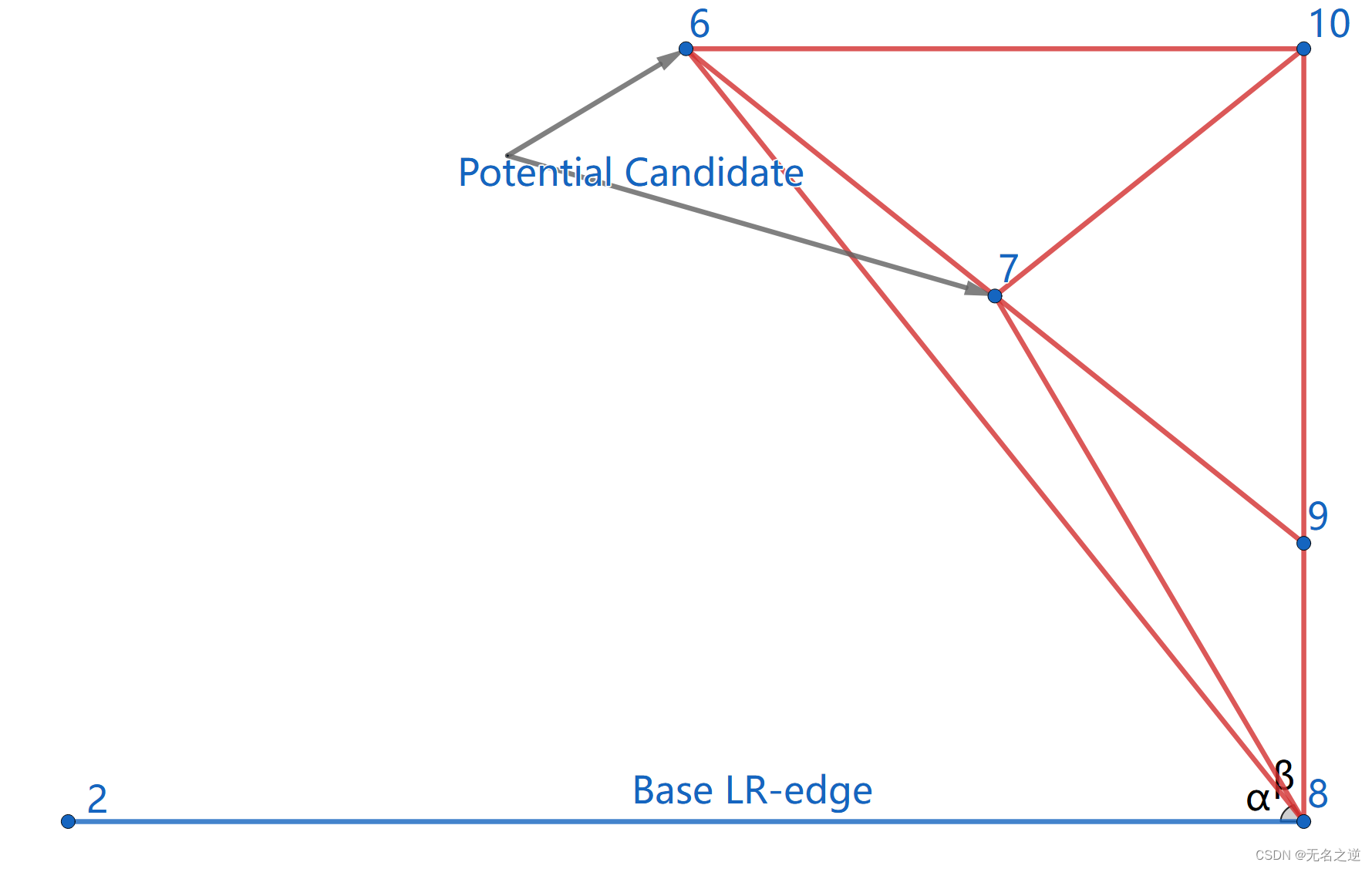
在这里插入图片描述

对于可能的端点，我们需要按以下两个标准检验：

其对应 RR-edge 与 base LR-edge 的夹角小于 $180$ 度。
base LR-edge 两端点和这个可能点三点构成的圆内不包含任何其它 可能点。

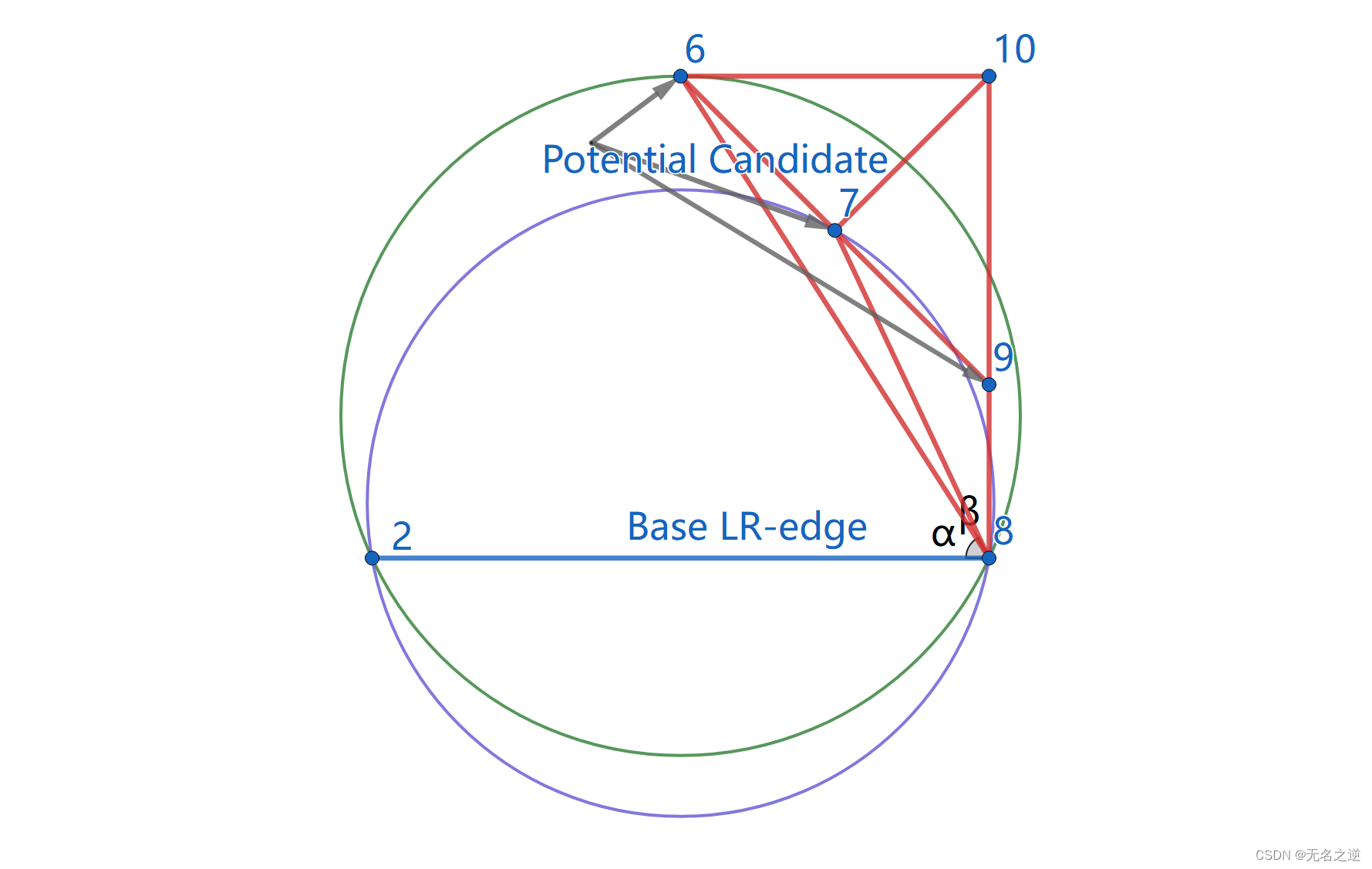
在这里插入图片描述

如上图， $6$ 号可能点所对应的绿色圆包含了 $9$ 号可能点，而 $7$ 号可能点对应的紫色圆则不包含任何其它可能点，故 $7$ 号点为下一条 LR-edge 的右端点。

对于左侧点集，我们做镜像处理即可。

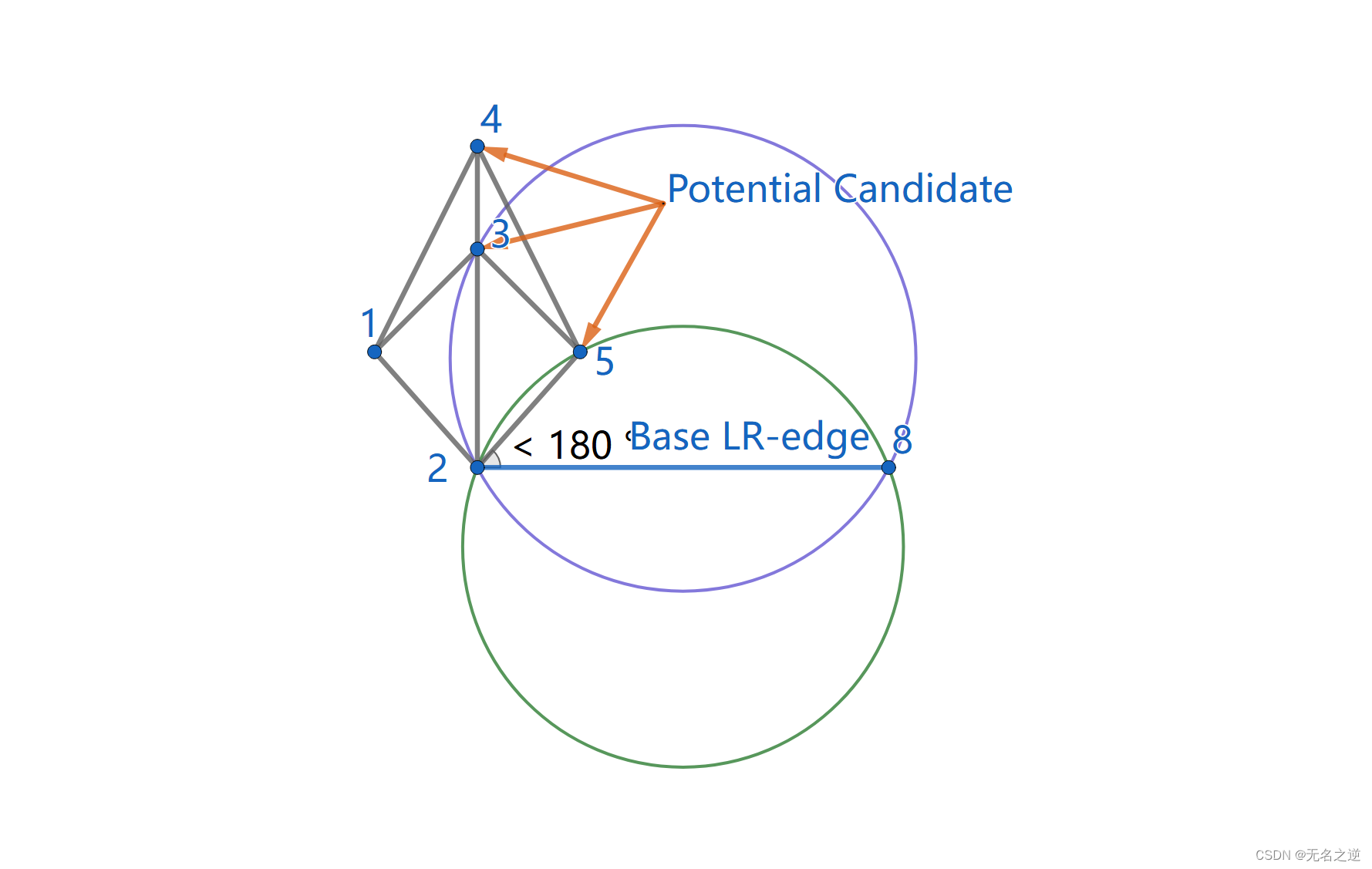
在这里插入图片描述

当左右点集都不再含有符合标准的可能点时，合并即完成。当一个可能点符合标准，一条 LR-edge 就需要被添加，对于与需要添加的 LR-edge 相交的 LL-edge 和 RR-edge，将其删除。

当左右点集均存在可能点时，判断左边点所对应圆是否包含右边点，若包含则不符合；对于右边点也是同样的判断。一般只有一个可能点符合标准（除非四点共圆）。

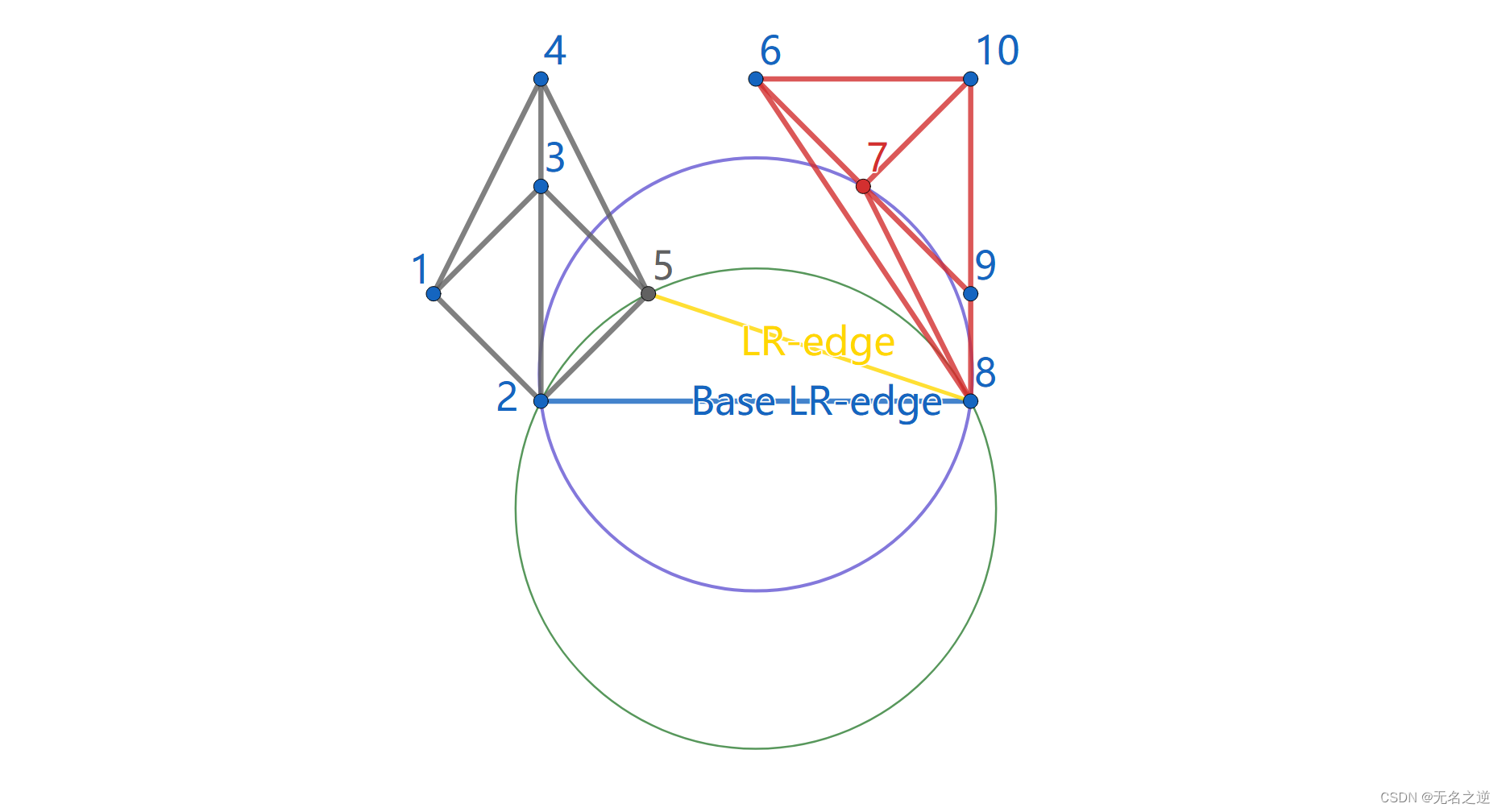
在这里插入图片描述

当这条 LR-edge 添加好后，将其作为 base LR-edge 重复以上步骤，继续添加下一条，直到合并完成。

在这里插入图片描述

代码

    #include <algorithm>#include <cmath>#include <cstring>#include <list>#include <utility>#include <vector>const double EPS = 1e-8;const int MAXV = 10000;struct Point {double x, y;int id;Point(double a = 0, double b = 0, int c = -1) : x(a), y(b), id(c) {}bool operator<(const Point &a) const {return x < a.x || (fabs(x - a.x) < EPS && y < a.y);}bool operator==(const Point &a) const {return fabs(x - a.x) < EPS && fabs(y - a.y) < EPS;}double dist2(const Point &b) {return (x - b.x) * (x - b.x) + (y - b.y) * (y - b.y);}};struct Point3D {double x, y, z;Point3D(double a = 0, double b = 0, double c = 0) : x(a), y(b), z(c) {}Point3D(const Point &p) { x = p.x, y = p.y, z = p.x * p.x + p.y * p.y; }Point3D operator-(const Point3D &a) const {return Point3D(x - a.x, y - a.y, z - a.z);}double dot(const Point3D &a) { return x * a.x + y * a.y + z * a.z; }};struct Edge {int id;std::list<Edge>::iterator c;Edge(int id = 0) { this->id = id; }};int cmp(double v) { return fabs(v) > EPS ? (v > 0 ? 1 : -1) : 0; }double cross(const Point &o, const Point &a, const Point &b) {return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);}Point3D cross(const Point3D &a, const Point3D &b) {return Point3D(a.y * b.z - a.z * b.y, -a.x * b.z + a.z * b.x,a.x * b.y - a.y * b.x);}int inCircle(const Point &a, Point b, Point c, const Point &p) {if (cross(a, b, c) < 0) std::swap(b, c);Point3D a3(a), b3(b), c3(c), p3(p);b3 = b3 - a3, c3 = c3 - a3, p3 = p3 - a3;Point3D f = cross(b3, c3);return cmp(p3.dot(f));  // check same direction, in: < 0, on: = 0, out: > 0}int intersection(const Point &a, const Point &b, const Point &c,const Point &d) {  // seg(a, b) and seg(c, d)return cmp(cross(a, c, b)) * cmp(cross(a, b, d)) > 0 &&cmp(cross(c, a, d)) * cmp(cross(c, d, b)) > 0;}class Delaunay {public:std::list<Edge> head[MAXV];  // graphPoint p[MAXV];int n, rename[MAXV];void init(int n, Point p[]) {memcpy(this->p, p, sizeof(Point) * n);std::sort(this->p, this->p + n);for (int i = 0; i < n; i++) rename[p[i].id] = i;this->n = n;divide(0, n - 1);}void addEdge(int u, int v) {head[u].push_front(Edge(v));head[v].push_front(Edge(u));head[u].begin()->c = head[v].begin();head[v].begin()->c = head[u].begin();}void divide(int l, int r) {if (r - l <= 2) {  // #point <= 3for (int i = l; i <= r; i++)for (int j = i + 1; j <= r; j++) addEdge(i, j);return;}int mid = (l + r) / 2;divide(l, mid);divide(mid + 1, r);std::list<Edge>::iterator it;int nowl = l, nowr = r;for (int update = 1; update;) {// find left and right convex, lower common tangentupdate = 0;Point ptL = p[nowl], ptR = p[nowr];for (it = head[nowl].begin(); it != head[nowl].end(); it++) {Point t = p[it->id];double v = cross(ptR, ptL, t);if (cmp(v) > 0 || (cmp(v) == 0 && ptR.dist2(t) < ptR.dist2(ptL))) {nowl = it->id, update = 1;break;}}if (update) continue;for (it = head[nowr].begin(); it != head[nowr].end(); it++) {Point t = p[it->id];double v = cross(ptL, ptR, t);if (cmp(v) < 0 || (cmp(v) == 0 && ptL.dist2(t) < ptL.dist2(ptR))) {nowr = it->id, update = 1;break;}}}addEdge(nowl, nowr);  // add tangentfor (int update = 1; true;) {update = 0;Point ptL = p[nowl], ptR = p[nowr];int ch = -1, side = 0;for (it = head[nowl].begin(); it != head[nowl].end(); it++) {if (cmp(cross(ptL, ptR, p[it->id])) > 0 &&(ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0)) {ch = it->id, side = -1;}}for (it = head[nowr].begin(); it != head[nowr].end(); it++) {if (cmp(cross(ptR, p[it->id], ptL)) > 0 &&(ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0)) {ch = it->id, side = 1;}}if (ch == -1) break;  // upper common tangentif (side == -1) {for (it = head[nowl].begin(); it != head[nowl].end();) {if (intersection(ptL, p[it->id], ptR, p[ch])) {head[it->id].erase(it->c);head[nowl].erase(it++);} else {it++;}}nowl = ch;addEdge(nowl, nowr);} else {for (it = head[nowr].begin(); it != head[nowr].end();) {if (intersection(ptR, p[it->id], ptL, p[ch])) {head[it->id].erase(it->c);head[nowr].erase(it++);} else {it++;}}nowr = ch;addEdge(nowl, nowr);}}}std::vector<std::pair<int, int> > getEdge() {std::vector<std::pair<int, int> > ret;ret.reserve(n);std::list<Edge>::iterator it;for (int i = 0; i < n; i++) {for (it = head[i].begin(); it != head[i].end(); it++) {if (it->id < i) continue;ret.push_back(std::make_pair(p[i].id, p[it->id].id));}}return ret;}};

Voronoi 图

Voronoi 图由一组由连接两邻点直线的垂直平分线组成的连续多边形组成，根据 $n$ 个在平面上不重合种子点，把平面分成 $n$ 个区域，使得每个区域内的点到它所在区域的种子点的距离比到其它区域种子点的距离近。

Voronoi 图是 Delaunay 三角剖分的对偶图，可以使用构造 Delaunay 三角剖分的分治算法求出三角网，再使用最左转线算法求出其对偶图实现在 $\log n)$ 的时间复杂度下构造 Voronoi 图。

推荐几款学习编程的免费平台

免费在线开发平台（https://docs.ltpp.vip/LTPP/）

       探索编程世界的新天地，为学生和开发者精心打造的编程平台，现已盛大开启！这个平台汇集了近4000道精心设计的编程题目，覆盖了C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#等众多编程语言，为您的编程学习之旅提供了一个全面而丰富的实践环境。
      在这里，您不仅可以查看自己的代码记录，还能轻松地在云端保存和运行代码，让编程变得更加便捷。平台还提供了私聊和群聊功能，让您可以与同行们无障碍交流，分享文件，共同进步。不仅如此，您还可以通过阅读文章、参与问答板块和在线商店，进一步拓展您的知识边界。
       为了提升您的编程技能，平台还设有每日一题、精选题单以及激动人心的编程竞赛，这些都是备考编程考试的绝佳资源。更令人兴奋的是，您还可以自定义系统UI，选择视频或图片作为背景，打造一个完全个性化的编码环境，让您的编程之旅既有趣又充满挑战。

免费公益服务器（https://docs.ltpp.vip/LTPP-SHARE/linux.html）

       作为开发者或学生，您是否经常因为搭建和维护编程环境而感到头疼？现在，您不必再为此烦恼，因为一款全新的免费公共服务器已经为您解决了所有问题。这款服务器内置了多种编程语言的编程环境，并且配备了功能强大的在线版VS Code，让您可以随时随地在线编写代码，无需进行任何复杂的配置。
随时随地，云端编码
       无论您身在何处，只要有网络连接，就可以通过浏览器访问这款公共服务器，开始您的编程之旅。这种云端编码的便利性，让您的学习或开发工作不再受限于特定的设备或环境。
丰富的编程语言支持
       服务器支持包括C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#等在内的多种主流编程语言，满足不同开发者和学生的需求。无论您是初学者还是资深开发者，都能找到适合自己的编程环境。
在线版VS Code，高效开发
       内置的在线版VS Code提供了与本地VS Code相似的编辑体验，包括代码高亮、智能提示、代码调试等功能，让您即使在云端也能享受到高效的开发体验。
数据隐私和安全提醒
       虽然服务器是免费的，但为了保护您的数据隐私和安全，我们建议您不要上传任何敏感或重要的数据。这款服务器更适合用于学习和实验，而非存储重要信息。

免费公益MYSQL（https://docs.ltpp.vip/LTPP-SHARE/mysql.html）

       作为一名开发者或学生，数据库环境的搭建和维护往往是一个复杂且耗时的过程。但不用担心，现在有一款免费的MySQL服务器，专为解决您的烦恼而设计，让数据库的使用变得简单而高效。
性能卓越，满足需求
       虽然它是免费的，但性能绝不打折。服务器提供了稳定且高效的数据库服务，能够满足大多数开发和学习场景的需求。
在线phpMyAdmin，管理更便捷
       内置的在线phpMyAdmin管理面板，提供了一个直观且功能强大的用户界面，让您可以轻松地查看、编辑和管理数据库。
数据隐私提醒，安全第一
       正如您所知，这是一项公共资源，因此我们强烈建议不要上传任何敏感或重要的数据。请将此服务器仅用于学习和实验目的，以确保您的数据安全。

免费在线WEB代码编辑器（https://docs.ltpp.vip/LTPP-WEB-IDE/）

       无论你是开发者还是学生，编程环境的搭建和管理可能会占用你宝贵的时间和精力。现在，有一款强大的免费在线代码编辑器，支持多种编程语言，让您可以随时随地编写和运行代码，提升编程效率，专注于创意和开发。
多语言支持，无缝切换
       这款在线代码编辑器支持包括C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#在内的多种编程语言，无论您的项目需要哪种语言，都能在这里找到支持。
在线运行，快速定位问题
       您可以在编写代码的同时，即时运行并查看结果，快速定位并解决问题，提高开发效率。
代码高亮与智能提示
       编辑器提供代码高亮和智能提示功能，帮助您更快地编写代码，减少错误，提升编码质量。

免费二维码生成器（https://docs.ltpp.vip/LTPP-QRCODE/）

       二维码（QR Code）是一种二维条码，能够存储更多信息，并且可以通过智能手机等设备快速扫描识别。它广泛应用于各种场景，如：
企业宣传
       企业可以通过二维码分享公司网站、产品信息、服务介绍等。
活动推广
       活动组织者可以创建二维码，参与者扫描后可以直接访问活动详情、报名链接或获取电子门票。
个人信息分享
       个人可以生成包含联系方式、社交媒体链接、个人简历等信息的二维码。
电子商务
       商家使用二维码进行商品追踪、促销活动、在线支付等。
教育
       教师可以创建二维码，学生扫描后可以直接访问学习资料或在线课程。
交通出行
       二维码用于公共交通的票务系统，乘客扫描二维码即可进出站或支付车费。        功能强大的二维码生成器通常具备用户界面友好，操作简单，即使是初学者也能快速上手和生成的二维码可以在各种设备和操作系统上扫描识别的特点。