算法体系-23 第二十三节：暴力递归到动态规划（五）

本文主要是介绍算法体系-23 第二十三节：暴力递归到动态规划（五），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一 求K次打击之后，英雄把怪兽砍死的概率

1.1 描述

给定3个参数，N，M，K

怪兽有N滴血，等着英雄来砍自己

英雄每一次打击，都会让怪兽流失[0~M]的血量

到底流失多少？每一次在[0~M]上等概率的获得一个值

求K次打击之后，英雄把怪兽砍死的概率

1.2 分析 尝试

第一砍可能让他掉0滴血到m滴血，就是0到m的展开，k次的话就是有（1+m）有k个相乘 math.pow(m+1,k)

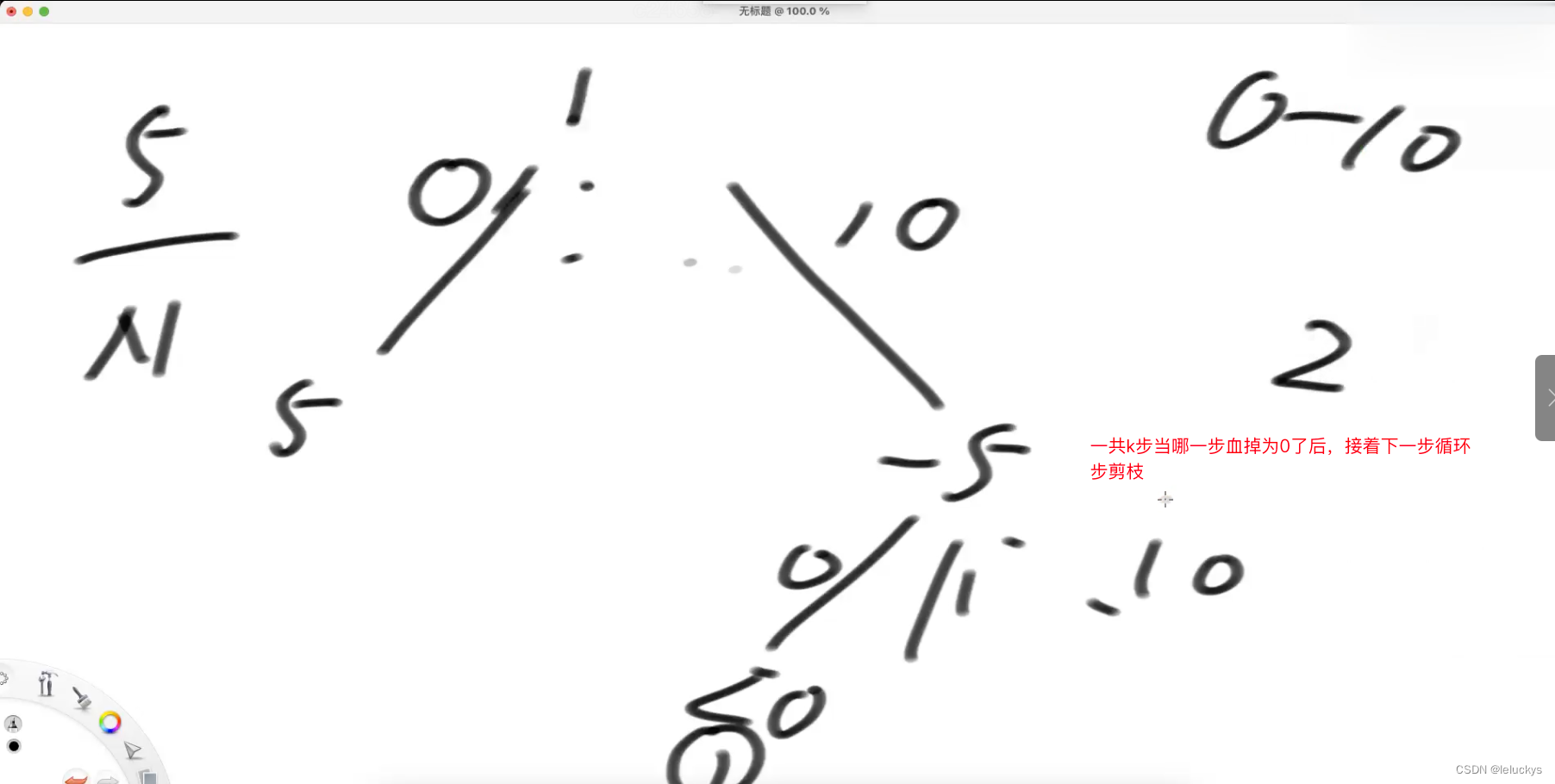
1.3 代码

    public static double right(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}long all = (long) Math.pow(M + 1, K);long kill = process(K, M, N);return (double) ((double) kill / (double) all);}// 怪兽还剩hp点血// 每次的伤害在[0~M]范围上// 还有times次可以砍// 返回砍死的情况数！public static long process(int times, int M, int hp) {if (times == 0) {return hp <= 0 ? 1 : 0;}//if (hp <= 0) {//return (long) Math.pow(M + 1, times);//}long ways = 0;for (int i = 0; i <= M; i++) {ways += process(times - 1, M, hp - i);}return ways;}

1.4 改动态规划

base条件是当前times==0 ，hp

hp - i 当 hp 剩余血量为0，但是还有3刀的情况那么hp - i就会越界

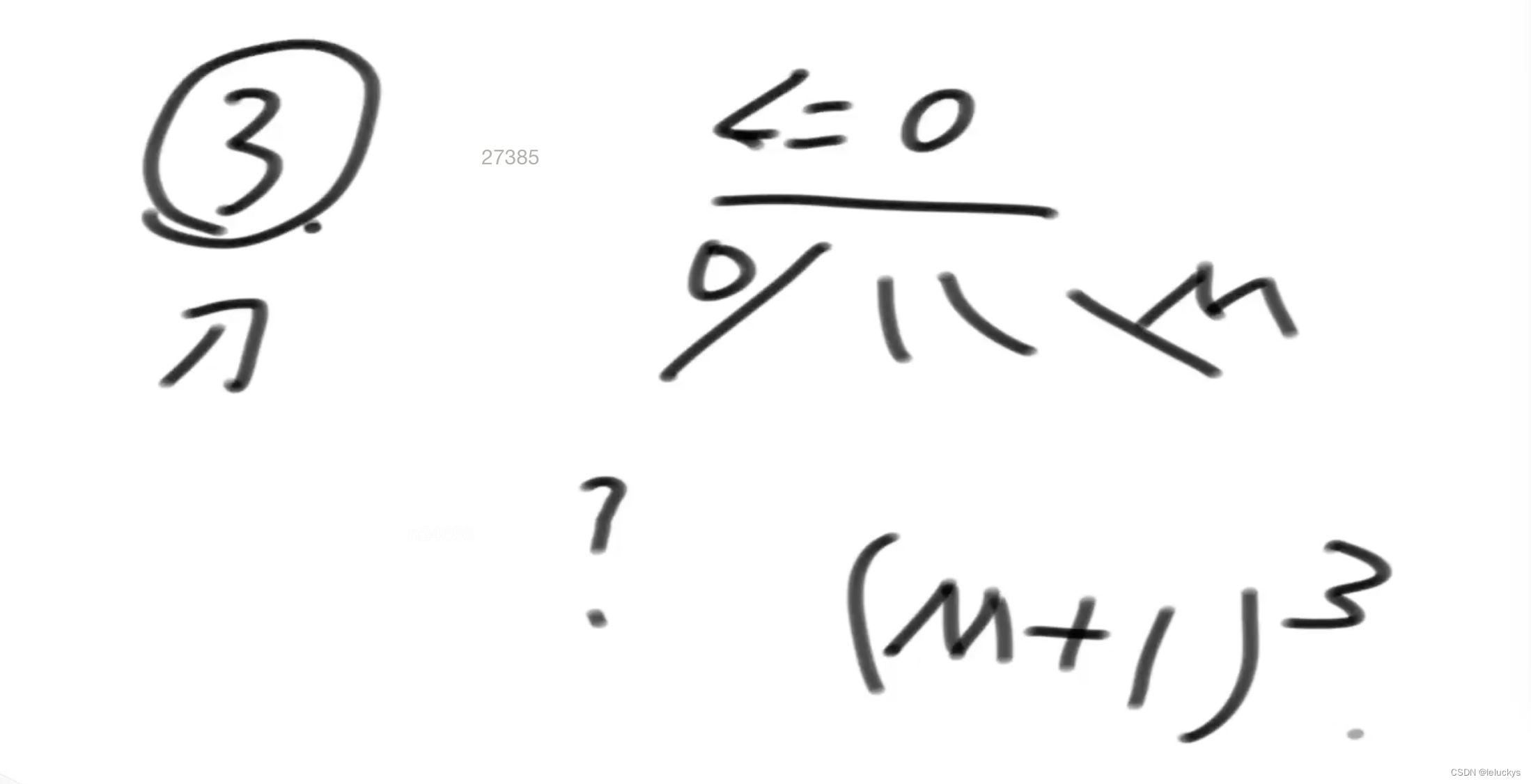
推表的时候，又出现小于的表的情况就剪支

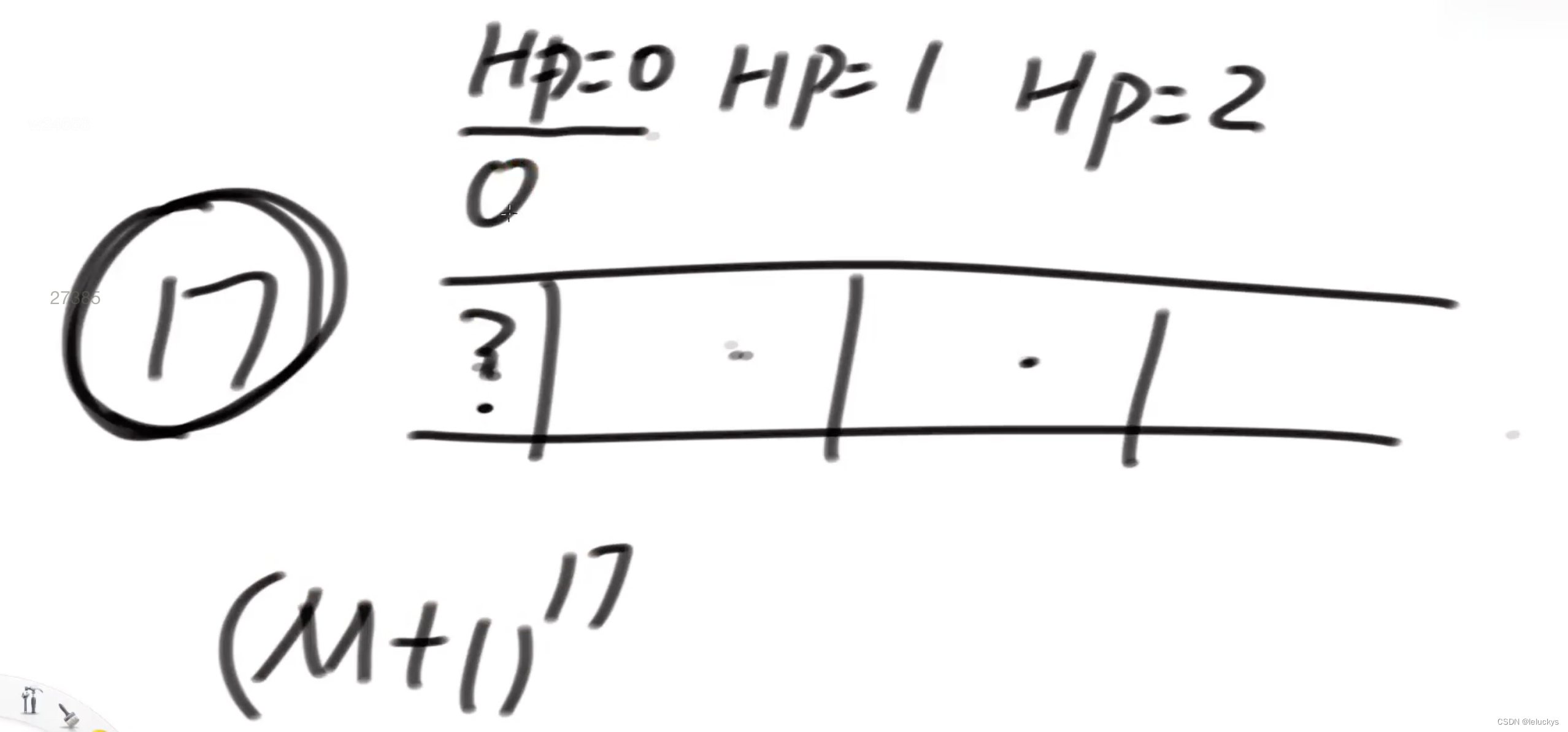
1.5 动态规划代码

public static double dp1(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}long all = (long) Math.pow(M + 1, K);long[][] dp = new long[K + 1][N + 1];dp[0][0] = 1;for (int times = 1; times <= K; times++) {dp[times][0] = (long) Math.pow(M + 1, times);for (int hp = 1; hp <= N; hp++) {long ways = 0;for (int i = 0; i <= M; i++) {if (hp - i >= 0) {ways += dp[times - 1][hp - i];} else {ways += (long) Math.pow(M + 1, times - 1);}}dp[times][hp] = ways;}}long kill = dp[K][N];return (double) ((double) kill / (double) all);}

这篇关于算法体系-23 第二十三节：暴力递归到动态规划（五）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---