本文主要是介绍论文学习 Learning Robust Representations via Multi-View Information Bottleneck,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Code available at https://github.com/mfederici/Multi-View-Information-Bottleneck
摘要:信息瓶颈原理为表示学习提供了一种信息论方法,通过训练编码器保留与预测标签相关的所有信息,同时最小化表示中其他多余信息的数量。然而,最初的公式需要标记数据来识别多余的信息。在这项工作中,我们将这种能力扩展到多视图无监督设置,其中提供了相同底层实体的两个视图,但标签未知。这使我们能够识别两个视图不共享的多余信息。理论分析导致了一个新的多视图模型的定义,该模型在Sketchy数据集和MIR-Flickr数据集的标签限制版本上产生最先进的结果。我们还利用标准数据增强技术将我们的理论扩展到单视图设置,与常见的无监督表示学习方法相比,经验显示出更好的泛化能力。
核心创新点:将两个视图学习得到的公共信息作为有用表征,将两个视图不共享的部分信息看作是冗余信息,最终两个视图之间相互学习得到标签信息丰富和鲁棒性强的表征。
1 INTRODUCTION
深度表征学习(LeCun et al., 2015)的目标是将原始观察输入x转换为通常较低维度的表征z,其中包含与给定任务或任务集相关的信息。通过监督表示学习在深度学习方面取得了重大进展,其中下游任务的标签y是已知的,而p(y|x)是直接学习的(Sutskever et al., 2012;Hinton et al., 2012)。由于获取大型标记数据集的成本,最近对无监督表示学习的重新关注旨在生成表示z,这对于各种不同的任务非常有用,这些任务几乎没有可用的标记数据(Devlin等人,2018;Radford等人,2019)。我们的工作基于信息瓶颈原则(Tishby et al., 2000),即通过丢弃输入中对给定任务无用的所有信息,表示受干扰的影响较小,从而提高了鲁棒性。在监督设置中,可以直接应用信息瓶颈原理,通过最小化数据x与其表示z之间的互信息,I(x;z),同时最大化z与标签y之间的互信息(Alemi et al., 2017)。在无监督设置中,只丢弃多余的信息更具挑战性,因为没有标签,模型无法直接识别哪些信息是相关的。近期文献(Devon Hjelm et al., 2019;van den Oord等人,2018)关注的是InfoMax目标最大化I(x, z),而不是最小化它,以保证所有预测信息都被表示保留,但不做任何事情来丢弃无关信息,本文将信息瓶颈方法推广到无监督的多视图设置中。为此,我们依赖于多视图文献的一个基本假设——每个视图提供相同的任务相关信息(Zhao et al., 2017)。因此,可以通过从表示中丢弃所有不被两个视图共享的信息来改进泛化。我们通过最大化两个视图表示之间的相互信息(多视图)来实现这一点,同时消除它们之间不共享的信息,因为这些信息肯定是多余的。生成的表示对于给定任务来说更加健壮,因为它们消除了特定于视图的麻烦。我们的贡献有三个方面:(1)我们将信息瓶颈原理扩展到无监督的多视图环境中,并对其应用提供了严格的理论分析。(2)我们定义了一个新模型1,该模型在两个标准多视图数据集Sketchy和MIR-Flickr的低标签设置下经验地得出了最先进的结果。(3)通过利用数据增强技术,我们的经验表明,我们的模型在单视图设置下学习的表征比现有的无监督表征学习方法更具鲁棒性,将我们的理论与增强策略的选择联系起来。
2 PRELIMINARIES AND FRAMEWORK
表征学习的挑战可以表述为找到一个分布p(z|x),该分布将数据观测值x∈x映射到表征z∈z,并捕获一些所需的特征。每当最终目标涉及到预测标签y时,我们只考虑足以识别y的z。这一要求可以通过考虑编码数据后仍然可访问的标签信息的数量来量化,并且被称为z对y的充分性(Achille & Soatto, 2018):
定义1。充分性:当且仅当I(x;y|z) = 0时,x的表示z对于y就足够了。任何访问足够表示z的模型都必须能够至少准确地预测y,就好像它可以访问原始数据x一样。事实上,当且仅当有关任务的信息量因编码过程而改变时,z 对于 y 就足够了(参见附录中的命题 B.1):
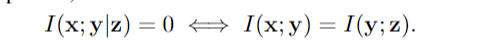
在足够的表示中,导致对未标记数据实例更好的泛化的表示特别吸引人。当 x 的信息内容高于 y 时,x 中的一些信息必须与预测任务无关。这可以通过使用互信息的链式法则将 I(x; z) 细分为两个组件来更好地理解(参见附录 A):
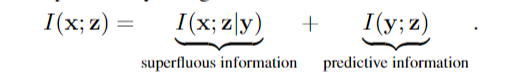
条件互信息I(x;Z |y)表示Z中不能预测y的信息,即多余信息。当我(y);Z)决定了有多少标签信息可以从表示中访问。请注意,最后一项与表示无关,只要z对y是充分的(参见公式1)。因此,当I(x;Z |y)最小。最小化多余信息的数量只能在监督设置中直接完成。实际上,减少I(x;z)在不违反充分性约束的情况下,必然需要对预测任务做出一些额外的假设(见附录中的定理B.1)。在下一节中,我们将描述我们技术的基础,这是一种通过利用数据上的附加视图形式的冗余信息,即使没有观察到标签y,也可以安全地减少表示的信息内容的策略。
3 MULTI-VIEW INFORMATION BOTTLENECK
作为一个激励的例子,假设v1和v2是同一物体从不同视点的两个图像,并设y为其标签。假设对象与v1和v2都明显不同,任何包含从两个视图都可访问的所有信息的表示z也将包含必要的标签信息。此外,如果z只捕获两个图片中可见的细节,它将消除特定于视图的细节,并降低表示对视图更改的敏感性。下面描述了支持这种直觉的理论,其中v1和v2被联合观察并称为数据视图。
3.1多视图设置中的充分性和鲁棒性在本节中,我们将充分性和极小性的分析扩展到多视图设置。直观地说,我们可以保证即使不知道y, z也足以预测y,只要保证z保持了v1和v2共享的所有信息。这种直觉依赖于多视图环境的一个基本假设——即两个视图提供相同的预测信息。为了形式化,我们定义了冗余。定义2。冗余性:v1相对于v2对于y是冗余的当且仅当I(y;直观地说,视图v1对于一个任务来说是冗余的,只要它与y的预测无关,如果v2已经被观察到。当v1和v2互为冗余时(v1相对于v2对于y是冗余的,反之亦然),我们可以证明如下:推论1。设v1和v2是目标y的两个相互冗余的视图设z1是v1的表示。如果z1对v2 (I(v1;v2|z1) = 0),则z1与两个视图的联合观测(I(v1v2;y) = I(y;z1))。换句话说,只要有可能假设相互冗余,任何包含两个视图共享的所有信息(冗余信息)的表示都与它们的联合观察一样具有预测性。通过将v1和z1之间的互信息类似于公式2分解,我们可以确定两个分量:
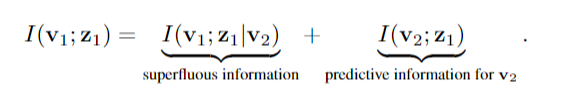
由于 I(v2; z1) 如果我们希望表示足以用于标签,我们得出结论,通过最小化 I(v1; z1|v2) 可以减少 I(v1; z1)。该术语直观地表示包含 v1 独有的信息 z1,并且通过观察 v2 无法预测。由于我们假设两个视图之间的相互冗余,因此该信息必须与预测任务无关,因此可以安全地丢弃。上述陈述和推论 1 的证明和形式断言可以在附录 B 中找到。两个视图共同点越少,在不违反标签的充分性的情况下,可以减少 I(v1; z1) 越多,因此,结果表示的鲁棒性越强。在极端情况下,v1 和 v2 只共享标签信息,在这种情况下,我们可以证明 y 的 z1 最小,并且我们的方法与监督信息瓶颈方法相同,而无需访问标签。相反,如果 v1 和 v2 相同,那么我们的方法退化为 InfoMax 原则,因为没有可以安全地丢弃信息(参见附录 E)。
3.2 多视图信息瓶颈损失函数给定满足标签 y 的相互冗余条件的 v1 和 v2,我们希望为 v1 的表示 z1 定义目标函数,该函数丢弃尽可能多的信息而不会丢失任何标签信息。在第 3.1 节中,我们展示了我们可以通过确保 v1 的表示 z1 足以满足 v2 来获得 y 的充分性,并且减少 I(z1; v1|v2) 将通过丢弃不相关的信息来增加表示的鲁棒性。因此,我们可以使用松弛拉格朗日目标结合这两个要求,以获得 v2 的最小充分表示 z1:


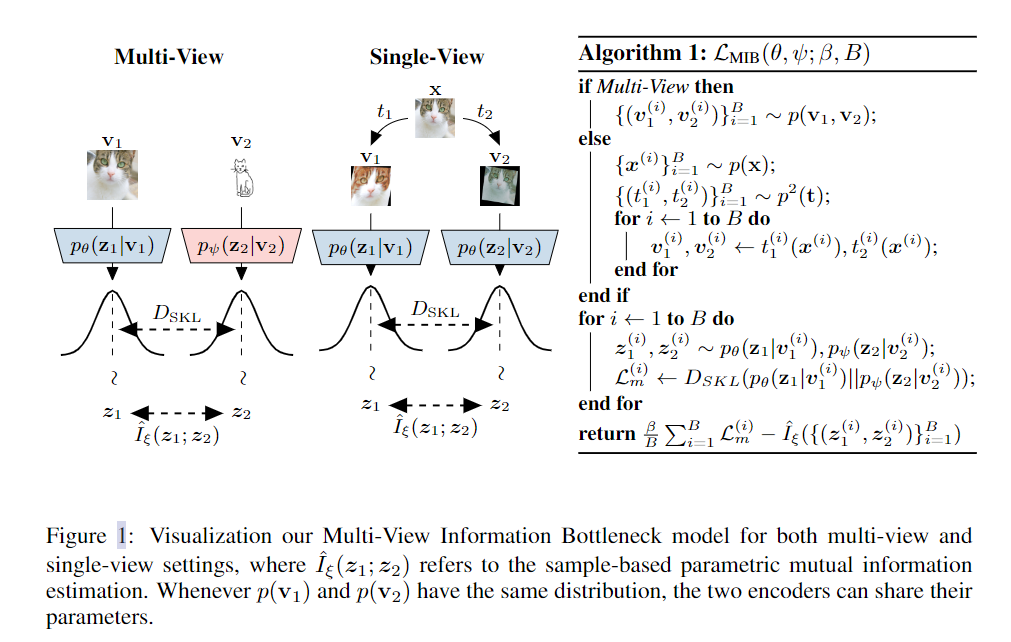
3.3 自我监督和不变性我们的方法也可以应用于通过利用标准数据增强技术无法获得多个视图时。这允许直接从增强数据中学习不变性,而不是要求它们构建到模型架构中。通过选择不影响标签信息的数据增强函数 t : X → W 的类 T,可以人为地构建满足 y 相互冗余的视图。设 t1 和 t2 是 T 上的两个随机变量,那么 v1 := t1(x) 和 v2 := t2(x) 对于 y 必须是相互冗余的。由于 T 中的数据增强函数不影响标签信息 (I(v1; y) = I(v2; y) =I(x; y)),足以用于 v2 的 v1 的表示 z1 必须包含与 x 相同数量的预测信息。该语句的正式证明可以在附录B.4中找到。每当相同观测的两个变换是独立的(I(t1;t2|x) = 0)时,它们会在两个视图中引入不相关的变化
例如,如果 T 表示一组小翻译,则两个生成的视图将因小移位而不同。由于此信息不共享,任何根据 MIB 目标最优的 z1 都必须丢弃有关位置的细粒度细节。为了实现编码器之间的参数共享,我们通过从具有相同概率的相同函数类 T 中独立采样两个函数来生成两个视图 v1 和 v2。因此,t1 和 t2 将具有相同的分布,因此两个生成的视图也将具有相同的边缘 (p(v1) = p(v2))。出于这个原因,两个条件分布 pθ (z1|v1) 和 pψ (z2|v2) 可以共享它们的参数,只需要一个编码器。只要两个视图具有相同的(或相似的)边际分布,就可以在多视图设置中应用完整(或部分)参数共享。
这篇关于论文学习 Learning Robust Representations via Multi-View Information Bottleneck的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








